3.2. Радиоактивность

Некоторые закономерности. Пробег и энергия, В большинстве случаев естественно радиоактивные превращения представляют собой -распад, что и приводит к уменьшению заряда ядра конечного продукта по сравнению с родоначальником семейства. Отличительной особенностью -распада является моноэнергетичность -частиц, испускаемых данным ядром, -частицы, испускаемые каким-либо ядром, имеют одну и ту же энергию, и следовательно, один и тот же пробег.

Некоторые элементы имеют -частицы с несколькими различными пробегами, и, следовательно, энергиями, например RaС или ТhС. Связь между энергией Е или скоростью v и пробегом R можно выразить законом Гейгера:

,

где

а = 9,610^-24 с³/м³.

Закон Гейгера — Нэттола. Гейгер и Нэттол установили очень важное соотношение между энергиями Е частиц и периодами полураспада. Обычно его выражают в виде связи между пробегом и постоянной распада:

К онстанта А, определяющая наклон прямой в координатах (1qR, lg), имеет практически одно и то же значение для всех трех радиоактивных рядов. В имеет различные значения для различных рядов (рис. 4). Закон ГейгераНэттола показывает, что ядра, испускающие -частицы с большей энергией, должны иметь меньший период полураспада, при этом небольшое различие в энергиях должно приводить к очень большому различию в периодах полураспада. Закон ГейгераНэттола использовался для определения периодов, полураспада некоторых элементов.

Теория -р а с п а д а. Объяснить -распад невозможно, если не привлекать волновых свойств частиц и следующий из них «туннельный» эффект. Действительно, еще из опытов Резерфорда известно, что -частицы с энергией 8,8Мэв рассеиваются ядрами урана в соответствии с их взаимодействием по закону Кулона, сближаясь при этом до расстояний ~310^12см. Это означает, что ядро окружено потенциальным барьером, высота которого не меньше 8,8Мэв. Вместе с тем сам уран испускает -частицы с энергией 4Мэв. Эту энергию -частица может приобрести, начиная движение с расстояния 610^12см. Чтобы объяснить, каким образом -частица из ядра попадает в область r610^12, минуя «запрещенную область» r<610^12 см, необходимо учесть «туннельный» эффект. Ядро окружено сферически симметричным потенциальным полем U(r), которое на больших расстояниях от ядра представляет собой кулоновское поле . Вблизи поверхности

ядра действуют большие силы притяжения — ядерные силы, аналитическое выражение для которых в настоящее время неизвестно. Но учитывая их большую величину и короткодействующий характер, потенциальную кривую вблизи ядра можно считать в виде ямы. В этой яме находится -частица с энергией Е, величина которой меньше высоты потенциального барьера. Это обеспечивает сравнительную устойчивость ядер к распаду. Но частица может выйти из ядра с энергией, меньшей высоты потенциального барьера.

Прозрачность барьера:

.

Она определяет вероятность для частицы пройти сквозь барьер при движении по радиусу. Но эта величина мала, поэтому частица отражается («отскакивает») от стенки потенциального барьера. Число ударов о стенку в единицу времени равно , где V  скорость -частицы.

В таком случае вероятность выхода из ядра -частицы в единицу времени составляет vD, но она равна также , следовательно,

= vD,

Или

.

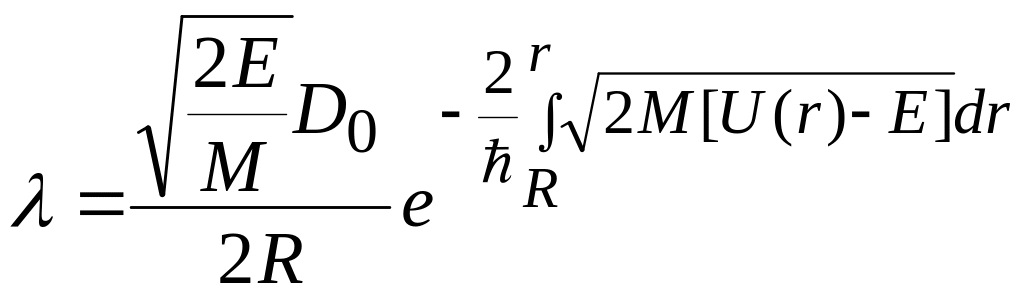Таким образом, это выражение дает связь между , энергией Е и радиусом потенциальной ямы R и заменяет собой приближенное выражение этой зависимости в законе ГейгераНэттола.

Определение радиуса потенциальной ямы ядра (радиуса ядра). В выражение для  входит энергия Е и радиус той области, где начинают действовать ядерные силы  R. Зная Е и , можно оценить R.

Спектр -ч а с т и ц. -частицы, испускаемые данным изотопом, имеют несколько различные энергии, как это доказано применением магнитных спектрометров. Различие в энергиях объясняется тем, что образующееся дочернее ядро может находиться в различных энергетических состояниях. Но помимо тонкой структуры спектра энергии, существует более значительное различие в энергиях  у некоторых элементов наблюдаются так называемые длиннопробежные -частицы, имеющие вполне определенную, но большую энергию, чем основная масса -частиц. Наличие таких частиц объясняется тем, что перед -распадом -частица может получить дополнительную энергию.

3.2.  - радиоактивность

-с п е к т р. -частицы имеют сплошной спектр энергии, в отличие от -частиц, имеющих линейчатый спектр. Распределение электронов по энергии при -распаде приведено на рис. 5. Кривая начинается от нуля, имеет максимум при некоторой энергии и определенный верхний предел Е_макс характерный для каждого изотопа. Величина Е_макс принимает значения от 15кэв до 15 Мэв.

Радиоактивный изотоп можно охарактеризовать средним значением энергии в спектре:

,

которое является характеристической величиной для данного ядра.

В явлении (-распада физики столкнулись с серьезной проблемой, касающейся закона сохранения энергии. Исходное и конечное ядра находятся во вполне определенных энергетических состояниях. Разность энергий исходного ядра и продукта распада, как показывают вычисления, равны максимальной полной энергии -частиц. Но калориметрические измерения, в которых все выделяемые электроны полностью поглощаются, показывают, что регистрируемая энергия совпадает не с максимальной, а со средней энергией, <Е>. Энергия Е_макс  <Е> как бы пропадает бесследно.

Налицо видимое нарушение закона сохранения энергии  одного из наиболее твердо установленных положений физики. Идея о нарушении закона сохранения энергии при -распаде, помимо ее методологической неприемлемости и противоречия с огромным опытным материалом, приводит к необъяснимости некоторых фактов самого распада. В качестве примера рассмотрим «ториевую вилку»:

.

ТhС может превратиться в ThD двумя путями: -распад + -распад или -распад + -распад. Энергия -частиц различна, -спектры также различны. Но сумма Е_а+ Е_макс для первого и второго пути одна и та же — 11,20 Мэв, что равно разности энергии ТhС и ThD. Если закон сохранении энергии при -распаде нарушается, то совпадение энергий для вилки кажется «чудом».

Закон сохранения спина. При -распаде из ядра вылетает электрон (или позитрон при ⁺-распаде искусственно радиоактивных ядер). Однако электронов в ядре нет. Электрон при -распаде рождается в момент распада, например, в результате превращения одного нейтрона в протон:

.

Электрон уносит момент количества движения , в то же время спин конечного ядра равен спину исходного ядра, так как массовое число ядра при -распаде не меняется. Таким образом, при -распаде закон сохранения момента количества движения как бы нарушается,

Нейтрино. Швейцарский физик Вольфганг Паули (1900—1958) предположил, что при -распаде из ядра вылетают две частицы: электрон и нейтрино v (точнее антинейтрино ). Гипотетическая частица нейтрино должна обладать при этом следующими свойствами: она должна быть нейтральной (так как z=(z+1)+^), иметь очень близкую к нулю массу покоя, спин ее равен , магнитный момент близок к нулю. Энергия ядра передается электрону Е(^) и нейтрино Е(v) так, что

Е(^)+Е( )=Е_макс.

В таком случае выполняются законы сохранения энергии и момента количества движения.

Отсутствие заряда (нейтральность) и малость магнитного момента нейтрино должны обеспечить малое взаимодействие нейтрино с веществом, что приводит к большому значению длины свободного пробега — в твердом теле до 10¹⁶км и полностью объясняет результат калориметрических опытов, в которых энергия нейтрино уносится ими из калориметра.