3. Порядок виконання розрахунково-графічної роботи

1.Намалювати заданий викладачем фрагмент схеми автоматизації.

2. Скласти логічну структурну схему надійності системи (фрагмента схеми).

3.Скласти таблицю значень інтенсивностей відмов елементів системи.

4. Записати формулу та побудувати графік імовірності безвідмовної роботи системи.

5. Зважаючи на умови експлуатації системи, запропонувати варіанти підвищення надійності за рахунок резервування різного виду.

6. Скласти логічну структурну схему надійності модифікованої системи.

7. Записати формулу та побудувати графік імовірності безвідмовної роботи модифікованої системи.

8. Зробити висновки про доцільність використаних видів резервування.

4. Приклад виконання завдання

Приклад виконання наводиться для схеми автоматизації процесу виробництва суспензійного полівінілхлориду.

Автоматична система регулювання процесу виробництва суспензійного полівінілхлориду, реалізована на локальних засобах автоматизації, складається з 70 елементів, на засобах мікропроцесорної техніки – з 51 відповідно. Інтенсивність відмов кожного елемента системи приведена нижче. З аналізу інтенсивності відмов елементів випливає, що для системи справедливим є експоненціальний закон надійності, отже відмова кожного елемента призводить до відмови всієї системи, тобто структурна логічна схема надійності системи представлена послідовним з’єднанням усіх елемен-

тів системи (див. рис. 4). На рис. 4 у прямокутниках розташований номер елемента, над ним – їх кількість.

Задачею даного дослідження є визначення методу підвищення надійності, при використанні якого імовірність безвідмовної роботи системи Pзад(t) на протязі 1000 годин була б не нижчою 0.99.

Вихідні дані для розрахунку:

де N1 – кількість елементів системи на локальних засобах автоматики;

N2 – кількість елементів системи виконаної на базі мікропроцесорної техніки;

t – наробіток системи;

Pзад(t) – імовірність безвідмовної роботи системи на протязі 1000 годин.

1

2

4

6

7

9

10

11

13

15

16

19

21

22

27

28

7 шт.

7 шт.

6 шт.

4 шт.

4 шт.

2 шт.

2 шт.

1 шт.

1 шт.

2 шт.

2 шт.

2 шт.

10 шт.

1 шт.

20 м

20 м

Рис. 4. Структурна логічна схема надійності:

а) системи на локальних засобах автоматики; б) системи, виконаної на базі мікропроцесорної техніки

1. Визначимо імовірність безвідмовної роботи системи до прийняття заходів по підвищенню надійності.

Розрахуємо інтенсивність відмов всієї системи реалізованій на локальних засобах автоматизації ( ) та за допомогою мікропроцесорної техніки ( ).

Зміна імовірності безвідмовної роботи від наробітку для систем, що розглядаються, наведена нижче і зображена на рис. 6.2.

Система з Рс1(1000) = 0.00004086 не задовольняє висунутим вимогам по надійності.

Система з Рс2(1000) = 0.0007466 не задовольняє висунутим вимогам по надійності.

2. Визначимо показники надійності, які повинна мати система, для того, щоб імовірність її безвідмовної роботи була не нижча 0.99.

Враховуючи властивість заміни експоненти двома членами ряду, на який вона розкладається при

маємо

.

Звідки

При цьому середній наробіток до відмови елементів повинен складати:

В реальній системі зниження середньої інтенсивності відмов елементів майже на два порядки ( ) практично неможливо. Якщо складність системи залишити незмінною, можливо зменшити та тільки на один порядок. Але у складній системі навіть однотипні елементи можуть працювати при різних коефіцієнтах навантаження, температурі зовнішнього середовища, вібрації, вологості тощо. Тому інтенсивності відмов однотипних елементів складної системи будуть різними. Отже, при підборі типів елементів розрахунок їх надійності виконується за інтенсивностями відмов з урахуванням умов їх експлуатації. Перерахунок інтенсивності відмов елемента у нормальних умовах на відповідні умови експлуатації виконується за формулою

,

де – поправковий коефіцієнт, що враховує вплив j-го фактора (вібрації, ударні навантаження, вологість, тиск та ін.); поправкові коефіцієнти для деяких факторів наведені в табл. Д.1.1-Д.1.3 (додаток 1); – поправковий коефіцієнт, що враховує відмінність режимів роботи від їх номінальних значень (kн – коефіцієнт навантаження, t - температура).

Так сумарний вплив механічних факторів (вібрація + ударні навантаження) на неамортизовану апаратуру в лабораторних умовах складає k1,k2=1; вологості 90-98% та температури С складає k3=2; висоти 0-1 км складає k4=1 і в кінцевому результаті дає нам поправковий коефіцієнт К=4, який вагомо впливає на інтенсивність відмов системи. Тому дуже важливим фактором є покращення умов експлуатації системи.

Крім того, для елементів, що встановлені на технологічному обладнанні нереальним є середній наробіток до відмови, що складає десятки тисяч годин.

Якщо вважати можливим зменшення середньої інтенсивності відмов елементів системи на один порядок (k=10) за рахунок покращення умов експлуатації (а саме : зменшення вібрації та ударних навантажень на обладнанні та трубопроводах, підтримання сталих значень температури та вологості, встановлення обладнання на оптимальній висоті), імовірність безвідмовної роботи при цьому складе:

Рис. 6.3. Залежність імовірності безвідмовної роботи систем Рс1 та Рс2 після зменшення інтенсивності відмов елементів систем на один порядок від часу

Очевидно, що зменшення середньої інтенсивності відмов елементів на один порядок сприяло значному збільшенню імовірності безвідмовної роботи системи (з Рс1(1000)= до Рс11(1000)=0.905 та з Рс2(1000)= до Рс11(1000)=0.905).

Визначимо, якою має бути складність системи, щоб метод зменшення інтенсивності відмов дозволив сконструювати систему з заданою імовірністю безвідмовної роботи

Отримані значення є нереалізовними. Автоматична система керування з такою кількістю елементів забезпечила б потрібну імовірність безвідмовної роботи, але не виконувала б свої функції.

Результати графічних залежностей імовірності безвідмовної роботи системи від кількості елементів N та усередненої імовірності безвідмовної роботи елементів P1(t) (рис. 6.4). З них видно, що спрощенням системи можна істотно підвищити надійність. Причому ефект тим більший, чим нижче надійність елементів і чим складніша система.

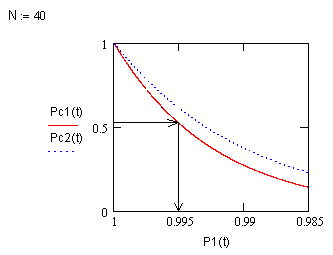
Рис. 6.4. Залежність імовірностей безвідмовної роботи локальної системи Рс1 та системи реалізованої на мікропроцесорній техніці Рс2 від кількості елементів N та імовірності їх безвідмовної роботи Р1

Користуючись отриманими залежностями можна легко визначити усереднену імовірність безвідмовної роботи елементів P1(t), знаючи імовірність безвідмовної роботи системи з кількістю елементів N.

3. Проаналізуємо метод підвищення надійності системи, який полягає у скороченні часу безперервної роботи.

Відомо, що у процесі експлуатації надійність будь-якої системи знижується. Змінивши сумарний час роботи системи, можна подовжити час її існування у працездатному стані.

Час безперервної роботи автоматичної системи скорочується внаслідок багаторазового її вмикання та вимикання. Це є можливим у тих випадках, коли для керування об’єктом немає необхідності тримати ввімкненою систему протягом всього часу функціонування об’єкта. Такими системами є, наприклад, системи корекції.

Однак зберегти надійність системи завдяки скороченню часу її безперервної роботи можна лише тоді, коли кількість вмикань та вимикань невелика. При частих вимиканнях і вмиканнях перехідні процеси можуть мати настільки сильний шкідливий вплив, що дискретний режим роботи системи стане недоцільним.

З врахуванням поставлених до системи вимог ( ) сумарний час неперервної роботи системи не повинен перевищувати

Якщо зменшити середню інтенсивність відмов елементів системи на один порядок, час t складе приблизно 100 годин.

4. Проаналізуємо метод підвищення надійності системи, який полягає у скороченні середнього часу відновлення.

Скорочуючи час відновлення системи, можна збільшити її готовність до роботи у будь-який момент часу, зменшити її простоювання, а отже, підвищити ефективність її функціонування.

5. Визначимо, як змінюються показники надійності системи при введенні резервних елементів.

При використанні методів підвищення надійності в першу чергу розглядається можливість розробки та використання високонадійних елементів, з яких складатиметься система, надалі – зміни конструкції та принципу дії системи і, нарешті, - впровадження резервування.

Найчастіше застосовується структурне резервування. Воно є найбільш характерним для локальних систем. При його використанні підвищення надійності досягається введенням в структуру системи додаткових елементів. Для систем, що розглядаються, неприйнятним є почасове резервування, оскільки в процесі виробництва полівінілхлориду не дозволяється перерва функціонування системи при відмові елемента.

З точки зору резервування всі елементи системи (табл. 1.1) можна розбити на такі групи:

1) елементи, відмова яких веде до зупинки технологічного процесу (критичні елементи);

2) елементи, відмова яких відмова яких веде до втрати інформації про технологічний процес.

До першої групи належать:

• первинні вимірювальні прилади (1, 4, 6, 9, 11, 13, 15, 19);

• регулятори та магнітні пускачі (22, 23, 24, 25, 26);

• проводи, кабелі (27, 28);

• регулюючі клапани (29).

До другої групи належать:

• вторинні показувальні та реєструвальні прилади (3, 5, 8, 10, 12, 14, 18, 20);

• перетворювачі (2, 7, 9, 16, 17, 21).

Відповідність елементів наведена у табл. 1.1.

Для кожної виділеної групи доцільним є певний вид резервування. Так, враховуючи вплив відмов елементів першої групи на дієздатність всієї системи для цієї групи оптимальним є постійне резервування («гарячий» резерв), при якому всі основні та резервні елементи працюють одночасно та з однаковим навантаженням. Відмови другої групи елементів не ведуть до зупинки технологічного процесу, тому для них доцільно виконати «холодний» резерв, при якому ненавантажений елемент не вмикається, поки не відмовить навантажений елемент. Для системи в цілому застосовується постійне резервування.

При загальному постійному резервуванні кількість резервних систем L визначається за формулою

0. Постійно ввімкнений резерв

Структурні схеми систем с постійно ввімкненим резервом зображені на рис. 6.5. Елементи з номером 1осн–26осн основні, а елементи з номерами 1р, 2р…Lp – резервними. Загальна кількість елементів в системі n = k+1, де k – кратність резервування – відношення кількості резервних елементів до кількості основних.

У даному випадку відмова системи наступає при відмові елемента з максимальним часом роботи.

На практиці найбільш часто мають місце випадки, коли основна система та всі резервні однакові та мають імовірність безвідмовної роботи P(t). Тоді

Вираз для інтенсивності відмов системи :

Рис. 6.5. Резервна система з постійно ввімкненим резервом: а) локальна система Рс1; б) система на базі мікропроцесорної техніки Рс2

З виразу (6.3) видно, що і з ростом t збільшується. Граничне значення: . Залежність інтенсивності відмов від часу приведена на рис. 6.6.

Рис. 6.6. Залежність інтенсивності відмов резервованої системи від часу

Імовірності безвідмовної роботи систем з постійно ввімкненим резервом Pc1 та Pc2 приведені на рис. 6.7.

а

б

Рис. 6.7. Залежність імовірності безвідмовної роботи від часу

а) систем з постійно ввімкненим резервом

б) нерезервованих систем та систем з постійно ввімкненим резервом

Оцінимо залежність імовірності безвідмовної роботи системи від часу і кратності загального резервування (рис. 6.8):

Оцінимо залежність імовірності безвідмовної роботи системи від часу і кратності загального резервування (рис. 6.8):

б

Рис. 6.8. Залежність імовірності безвідмовної роботи системи від часу і кратності загального резервування

а) локальна системи Рс1;

б) система на базі мікропроцесорної техніки Рс2

ВИСНОВКИ

З отриманих результатів можна зробити висновки:

1) імовірність безвідмовної роботи резервованої системи завжди більша від імовірності безвідмовної роботи нерезервованої системи, причому чим вище кратність резервування, тим більшою є Рс (t); залежності Рс( ) для великих наближаються до експоненти і до функції імовірності безвідмовної роботи нерезервованої системи;

2) середній час безвідмовної роботи системи при збільшенні кратності резервування зростає дуже повільно;

3) інтенсивності відмов резервованої системи починається з нуля і наближається в області великих значень до інтенсивності відмов нерезервованої системи (L=0);

4) ефективність резервування полягає в тому, що воно значно поліпшує основні кількісні характеристики надійності в області малих значень .

5) постійне резервування для всієї системи є дорогим і не досить доцільним заходом і є більш прийнятним для першої резервної групи системи.