2.2 Туннельный эффект

Туннельный эффект - чисто квантово-механическое явление, не имеющее аналога в классической физике. Напомним, с классической точки зрения полная энергия частицы, движущейся в потенциальном силовом поле, выражается:

, (1),

где m – масса частицы, – скорость, Е – полная энергия частоты, u(x) – ее потенциальная энергия как функция координат. Для простоты мы ограничимся случаем одномерного движения. Переписав (I) в виде

приходим к выводу, что движение частицы возможно в тех областях пространства, где Е  u(x). (2). Величина Е задается начальными условиями и остается постоянной за все время движения, u(x)  определяется геометрией силового поля (однородное, центрально-симметричное и т.д.), поэтому разность Еu(x) изменяется от точки к точке, изменяется, поэтому и скорость частицы, хотя в любой момент .(3). Пусть в некотором потенциальном силовом поле зависимость u(x) имеет вид, изображенный графически на рис.1. По оси ординат будем откладывать u(x) и Е. Понятно,

ч то график Е(х) параллелен оси х. Если начальные условия таковы, что Е = Е₁, то частица может оказаться в любой точке интервала (x₁, ). Если Е = Е₂, то условие (2) выполняется только в интервалах (х₂, х₃) или (х₄,. ). Если Е = E₃, то частицу могло обнаружить или в интервале (х₅, х₆), или([х₇, х₈), в зависимости от того, куда ее поместили в начале движения. Проникнуть в те области, где Е<u(x) частица без внешних воздействий не может.

Опыт показывает, что свойства элементарных частиц гораздо богаче, чем описано выше, в частности, они носят волновой и вероятностный характер и проявляются только в определенных условиях. Уравнения классической механики не отражают этого богатства свойств.

О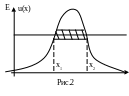 бобщение опытных данных по движению микрочастиц привело к более общему закону природы, чем законы Ньютона, который выражается уравнением Шредингера. Решение уравнения Шредингера для движения микрочастицы в области пространства, где существует потенциальный барьер, не запрещает частице оказаться по другую сторону барьера без внешних воздействий. Экспериментальные данные показывают, что действительно, микрочастицы могут двигаться в области (, +), они как бы просачиваются через барьер (рис.2). На образном языке говорят, что частицы проходят через туннель в барьере (интервал (х₁, х₂)), откуда и название явления  туннельный эффект. Как и другие явления квантовой механики, он носит вероятностный характер, это значит, что существует отличная от нуля и меньшая единицы, вероятность туннелирования частицы. Эту вероятность D называют коэффициентом прозрачности барьера. Прозрачность барьера растет по мере приближения Е к w и довольно велика для легких частиц и очень тонких барьеров, порядка 10^-10 м.

С классической точки зрения туннельный эффект представляется абсурдным, так как частица, "находящаяся в туннеле", должна была бы обладать отрицательной кинетической энергией (в туннеле Е < u). В квантовой механике деление полной энергии на кинетическую и потенциальную не имеет смысла, так как противоречит принципу неопределенности. Действительно, тот факт, что частица обладает определенной кинетической энергией Т, был бы равнозначен тому, что частица имеет определенный им u означал бы, что частица находится в точно заданном месте пространства. Поскольку координата и импульс частицы не могут одновременно иметь определенных значений, не могут быть одновременно точно определены Т и u. Таким образом, хотя полная энергия частицы Е имеет вполне определенное значение, она не может быть представлена в виде суммы точно определенных энергий Т и u. Ясно, что при такой ситуации заключение об отрицательности Т в туннеле становится беспочвенным.

Рассмотрим теперь это явление на более глубоком математическом аппарате и на конкретных моделях потенциальных барьеров, уточнив одновременно физический смысл отдельных параметров.

Пусть частица массы и энергии движется вдоль оси , и на своем пути встречает потенциальный барьер в виде прямоугольной ступеньки ширины и высоты (рис.4) т.е.

(4)

Рассмотрим вначале случай, когда , т.е. туннелирование частиц. Основным количественным параметром, характеризующим этот эффект, является коэффициент проницаемости (прозрачности) барьера , который определяется как отношение потока частиц за барьером (область III) к потоку падающих на барьер частиц (область I, исключая отраженные волны). Для оценок параметра необходимо провести следующие расчеты:

а) для заданного потенциала (4) записать стационарное, одномерное уравнение Шредингера;

б) найти решения этого уравнения для всех трех областей ;

в) удовлетворить стандартным условиям, накладываемым на волновую функцию, в частности, условиям непрерывности и на границах областей:

; (5)

г) для полученных волновых функций вычислить плотность тока вероятности I и III согласно соотношению

. (6)

В частности, для волновых функций экспоненциального типа

; (7)

д) вычислить коэффициент проницаемости барьера .

Данная программа описана во всех руководствах по квантовой механике, поэтому приведем лишь краткое описание этих этапов.

а) Динамика движения микрочастицы в одномерном потенциальном поле описывается стационарным уравнение Шредингера:

, (8)

которая для всех трех областей с потенциалом (4) приводится к виду:

, (9)

где введены обозначения

(10)

б) Решения уравнения (9) в общем виде имеют вид:

(11)

Решения имеют смысл падающих и отраженных плоских волн де Бройля (без временной зависимости). В силу однородности пространства за барьером (III область) отсутствуют отраженные волны, поэтому необходимо положить . Тогда с учетом соотношений (10), решения уравнения Шредингера окончательно можно представить в виде:

(12)

в) Для определения остальных коэффициентов и запишем граничные условия (2):

(13)

Решая однородную систему алгебраических уравнений, можно найти искомые коэффициенты , в частности:

.(14)

г) Так как падающие и отраженные волны имеют экспоненциальный характер, то в соответствии с формулой (7)

.

д) Отсюда для коэффициента проницаемости с учетом (14) окончательно получаем:

. (15)

Примем во внимание, что в большинстве задач микромира можно заменить на . Действительно, например, в атомной физике, полагая эВ, м параметр

и таким образом . Следовательно, точную формулу (15) можно существенно упростить:

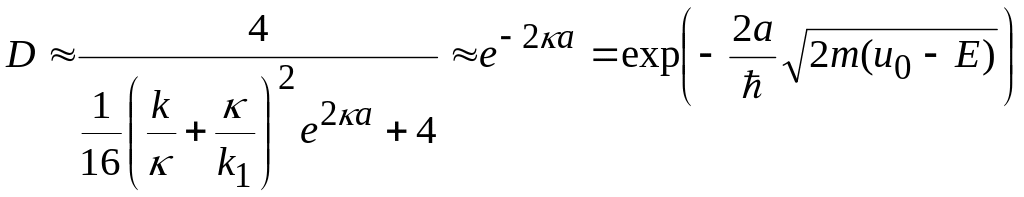. (16)

т.е. с точностью до несущественного множителя перед экспонентой коэффициент проницаемости можно описать приближенной формулой (16).

Рассмотрим теперь надбарьерное отражение т.е. случай, когда . Очевидно и сейчас уравнение Шредингера имеет прежний вид (9) с решениями (11). Однако параметр (10) становится действительным числом, при этом соотношение (15) сохраняет свой вид при замене на . С учетом очевидного условия

для коэффициента проницаемости получаем выражение вида:

. (17)

Из соотношения (17) следует, что частица беспрепятственно пролетает над барьером, как и в классическом случае , если (что физически свидетельствует об отсутствии потенциальной ступеньки , либо когда , что соответствует энергии (см.7)

, (18)

совпадающей с уровнями энергии в бесконечно глубокой потенциальной яме. В остальных случаях и частица испытывает так называемое надбарьерное отражение. Этот эффект также отсутствует в классической физике.