1.3 Определение значений флуктуирующих величин

Как известно, при любом физическом измерении результат, полученный на опыте, несколько отличается от действительного (истинного) значения измеряемой величины. Погрешности измерений складываются из ошибок, связанных с несовершенством методики измерений и неточностью приборов (систематические ошибки), и из случайных ошибок эксперимента, изменяющих свою величину и знак от опыта к опыту. Использование метода многократных измерений позволяет достичь двух целей: 1.Уменьшить величину случайной ошибки; 2. Получить данные для расчета значения этой ошибки.

До сих пор мы молчаливо подразумевали, что истинное (действительное) значение измеряемой величины существует, как отражение реальных свойств Природы. На самом деле, плотность некоторого вещества, температура его фазовых переходов в заданных условиях, расстояния между географическими и астрономическими объектами в данный момент времени и многое, многое другое имеют свое истинное значение. Роль этого истинного значения мы приписываем:

- в случаях однократных измерений – результату этого однократного измерения, располагая его в интервале систематических ошибок;

- в случаях многократных измерений – среднему значению измеряемой величины, располагая его в интервале случайных ошибок, найденному методами расчета границ, либо подсчета значащих цифр, либо дифференцирования и т.д.

Теперь же мы рассматриваем явления, которым самой Природой предписан вероятностный (случайный) характер. Для них в принципе не существует истинных, не изменяющихся со временем, некоторых количественных параметров. Соответствующие ошибки называются флуктуациями самой измеряемой величины. С понятием «флуктуация» Вы уже встречались в молекулярной физике, в разделах, посвященных статистическим методам исследования. Распады атомных ядер – это также случайные во времени процессы. Поэтому к флуктуирующим величинам относится, например, и интенсивность радиоактивного излучения. Пусть при некотором измерении зарегистрировано n частиц. Из этого отнюдь не следует, что в любые следующие такие же промежутки времени будет регистрироваться именно n частиц. Легко убедиться, что в разных, отдельных опытах, проведенных в одинаковых условиях, мы будем получать другие, хотя и не слишком отличающиеся от n, числа.

Возникают вполне естественные вопросы: Как интерпретировать результаты наших измерений? Какие преимущества мы получим, проводя опыты несколько раз, по сравнению с однократным измерением? Как долго нужно проводить однократное измерение в серии многократных измерений? Сколько раз его необходимо повторить, чтобы использовать преимущества многократного метода?

Для простоты дальнейших рассуждений перейдем от понятия «интенсивность радиоактивного излучения» к численно пропорциональным ему понятиям «число частиц, зарегистрированных некоторым счетчиком за некоторый промежуток времени» и «скорость счета частиц этим же счетчиком». Понятно, что скорость счета – это частное от деления числа частиц на время счета этого числа.

Проведем большое количество измерений числа частиц, попадающих в счетчик за некоторое время t. Авторы проводили реальный эксперимент, отсчитывая количество частиц N за каждые последующие 10 секунд 60 раз. Часть полученных данных приведена ниже в табличной форме, где № - порядковый номер опыта:

№	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	…60
N	14	9	14	10	9	13	9	9	12	6	9	7	6	4	7	8	4	4	7	10

Всего было насчитано 539 частиц. Сравнив полученные результаты, мы увидим, что данные числа заметно отличаются друг от друга, хотя среди них встречаются и одинаковые. Отличаются они и от среднего значения, рассчитанного по всем опытам: N_ср=539/60; т.е. N_ср=8,98. Кроме этого авторы подсчитали средние значения числа зафиксированных частиц для отдельных серий опытов: с первого по пятнадцатый, с шестнадцатого по тридцатый, с первого по тридцатый и т.д. Были получены следующие результаты:

Диапазон номеров опытов	1-15	1-30	1-45	16-30	16-45	16-60	30-45	30-60	45-60
Nср по данному диапа­зону	9,20	8,90	8,66	8,60	8,40	8,91	8,20	9,07	9,93

Приведенные в таблицах данные хорошо подтверждают случайный во времени характер радиоактивности атомных ядер. Эти данные никак не могут быть представлены аналитически; в них нет никаких закономерностей. Тем не менее, существуют способы описания и таких природных явлений.

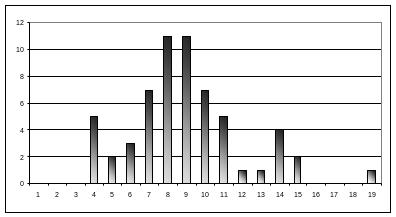
Продолжая анализировать результаты проведенных опытов, обратимся к методам статистики. Подсчитаем сколько раз (w) в этих опытах фиксировалось одинаковое число частиц N. Так, например, 4 частицы было отмечено 5 раз, 8 частиц – 11 раз, 12 частиц – 1 раз и т.д. Ниже приведены полные сведения об этом расчете. Последние строки в таблице – это относительное число, интересующих нас случаев: W= w/60 (округление до сотых); W%=100W (округление до целых).

N	4	5	6	7	8	9	10	11	12	13	14	15	19
w	5	2	3	7	11	11	7	5	1	1	4	2	1
W	0,08	0,03	0,05	0,12	0,18	0,18	0,12	0,08	0,02	0,02	0,07	0,03	0,02
W%	8	3	5	12	18	18	12	8	2	2	7	3	2

Снова видно отсутствие какой либо закономерности. Это можно подтвердить и графически. Отложим по оси абсцисс все числа N, т.е. количество частиц, зарегистрированных при измерениях в отдельных опытах в течение 10 секунд, а по оси ординат – число случаев w, в которых было зафиксировано данное количество частиц. На графике в виде гистограммы прямоугольник, расположенный между 0 и 1, характеризует случаи, в которых регистрировалось 0 отсчетов (у нас их не было); прямоугольник, расположенный между 1 и 2, - случаи с одним отсчетом и т.д. Результаты опыта можно проиллюстрировать и обычным графиком, т.е. гладкой кривой, проведенной через соответствующие точки.

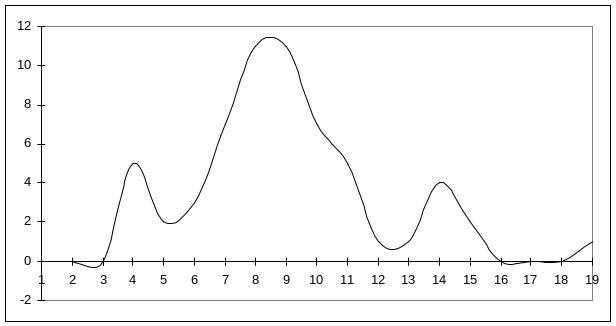
Мы получили графики распределения результатов опыта, которые имеют максимум и характерно, что он расположен вблизи области всех ранее рассчитанных средних значений. Среди результатов попадаются и такие, которые сильно отличаются от среднего; именно они затрудняют возможность представить данное распределение аналитически. В целях выполнения такой задачи поступим далее следующим образом: Будем считать, что измерения проводились не 60 раз в течение 10секунд каждое, а 30 раз по 20 секунд. Методика проведения опытов позволяет сделать это, поскольку при измерениях счетчик работал непрерывно в течение 600 секунд, а экспериментатор каждые 10 секунд записывал его показания. Он мог это делать и через каждые 20, 30, 40 секунд и т.д. На рисунках, приведенных ниже, отражены «последствия» таких действий.

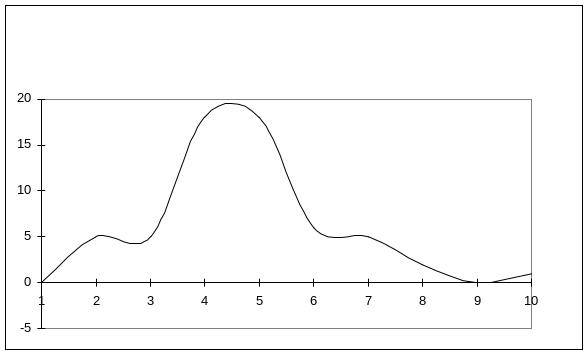
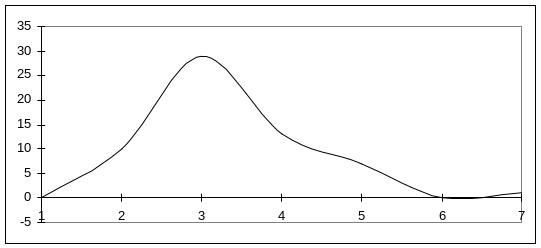
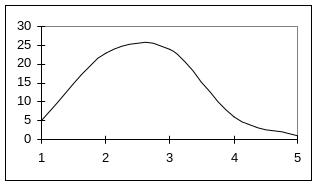
Хорошо видно, что в двух последних случаях распределения уже могут быть описаны достаточно простыми формулами (в предпоследнем случае можно исключить из рассмотрения результат одного опыта N =19, считая его промахом; это, кстати, можно было сделать и на самом первом этапе наших рассуждений). Распределения подобного вида известны в статистике как распределение Пуассона. Его формула:

w = (N_ср)^N / N!е ^Nср

Статистика оперирует и другими видами распределений случайных величин. Одно из них – нормальное – очень интересно в целях решения поставленных выше задач. Это распределение выражается формулой, весьма близкой к формуле распределения Пуассона:

w = 1 / σ √2πexp (N/2 σ²), где σ – стандартное отклонение.

График этой функции симметричная плавная кривая, имеющая максимум, который лежит на оси симметрии. Расположение этого максимума совпадает со средним значением результатов всех измерений N.

Физический смысл обеих распределений в приложении к нашей задаче – это относительное количество случаев (из всех наших шестидесяти опытов), в которых зафиксировано именно N частиц. В терминологии теории вероятностей это звучит так: распределение Пуассона и нормальное распределение описывают вероятность того, в данном конкретном опыте (из наших шестидесяти) будет зафиксирован точно N частиц. Разумеется, что чисто в математическом отношении их смысл формулируется в самом общем виде: статистические распределения показывают вероятность наступления некоторого благоприятного события из многих возможных. Например, вероятность достать из колоды карт конкретную карту, вероятность встретить в лесу дерево заданного диаметра, вероятность того, что в коллективе сотрудников работает человек строго определенного возраста и т.д. Понятно, что переменные в соответствующих математических формулах показывают характеристики изучаемых объектов.

Почему мы остановились на двух распределениях, а не на каком либо одном? Дело в том, что радиоактивность, что можно показать достаточно строго, подчиняется распределению Пуассона, описывающего дискретные случайные величины. Однако, его характеристики относительно сложны для анализа интересующих нас явлений. В этом отношении нормальное распределение, описывая непрерывные случайные величины, по своим свойствам несколько проще. Кроме преимуществ, связанных с его симметричным видом, оно обладает замечательным свойством: почти 68% всех описываемых им событий отличаются по величине от среднего значения не более чем на одно стандартное отклонение, а 95% – не более чем на два стандартных отклонения. В пределах трех отклонений находятся практически все события (более 99%). Поскольку нормальное распределение и распределение Пуассона довольно близки друг к другу, как по виду соответствующих формул, так и по виду гистограмм и «обычных» графиков, то можно ожидать, что указанное свойство присуще и радиоактивности. Давайте проверим на частном случае нашего опыта. Итак: среднее значение всех наших измерений – N_ср=8,98 или, округляя N_ср=9,0. Известно, что стандартное отклонение не превышает значения √ N_ср , т.е. равно трем. Из третьей из приведенных выше таблиц видно, что 45 случаев (а это – 75% от числа всех измерений) содержат результаты опытов, в которых было зафиксировано 6, 7, 8 ,9, 10, 11 или 12 частиц. Только в одном случае зафиксировано число частиц, которое не попадает в диапазон от трех до пятнадцати (это диапазон, границы которого отличаются от среднего значения на два стандартных отклонения). Таким образом, то распределение частиц, которое мы получили экспериментально, с большим «запасом» обладает свойством, присущим нормальному распределению. Результат, конечно, не вполне ожидаем, поскольку соответствующие график имеет два «лишних» максимума. Кстати, совокупность всех графиков показывает, что измерения на данной экспериментальной установке целесообразнее было проводить каждый раз не по 10, а по 30 секунд. Соответствующая кривая имеет вполне симметричный вид без лишних максимумов и перегибов, т.е. может быть описана распределением Пуассона.

Далее учтем, что количество частиц, зарегистрированных счетчиком, само по себе не несет информации о свойствах излучения. Нам важно знать количество частиц, излучаемых (и соответственно зафиксированных счетчиком) в единицу времени, т.е. определить скорость счета частиц, что позволит перейти при необходимости к расчету интенсивности радиоактивного излучения некоторым источником.

Будем сопровождать дальнейшие рассуждения мысленным опытом, который проведем по выше описанной методике реального эксперимента. Пусть всего было проделано К измерений в течение времени τ каждое и всего было зарегистрировано N частиц . Следовательно все время измерений t=К τ. В отдельных измерениях фиксировалось N₁, N₂, N₃,… N_К частиц, а их среднее значение можно определить по формулам:

N_ср = N / К или N_ср = (N₁+ N₂+N₃ +… + N_К) / К

Учтем, что каждое из измеренных количеств частиц отличается от среднего значения не более чем на √ N_ср (величина, так называемого стандартного отклонения) с вероятностью около 70%.

Проведя все измерения, перейдем к расчету скорости счета числа частиц. Разумеется, нас интересует ее среднее значение:

V_ср= N/ t или V_ср= (N₁+ N₂+N₃ +… + N_К) / К τ или V_ср= N_ср / τ

Абсолютная погрешность определения скорости счета частиц:

∆V_ср = ∆N_ср / τ, то есть ∆V_ср = √ N_ср / τ

Относительная погрешность скорости счета частиц определяется следующей цепочкой очевидных соотношений:

ε (V_ср) = ∆V_ср/ V_ср ε (V_ср) =(√ N_ср/ τ) / ( N /К τ)

ε (V_ср) = К τ √ N_ср / N τ ε (V_ср) =К/√ N

Поскольку мы стремимся к уменьшению погрешности измерений, то вполне естественно выбрать К=1. Таким образом, наименьшая относительная погрешность измерения скорости счета частиц в процентах определяется соотношением:

ε (V_ср)_% =100/√ N

Теперь мы можем ответить на оставленные ранее вопросы.

Как интерпретировать результаты наших измерений? Опираясь на статистические методы. Учитывать, что любая количественная оценка изучаемых явлений носит вероятностный характер. Указывая некоторый интервал, в котором находится значение измеренной нами величины, следует хорошо понимать, что при последующих каких либо измерениях существует отличная от нуля вероятность не попасть в этот интервал. А вот оценка значения этой вероятности поддается расчету.

Какие преимущества мы получим, проводя опыты несколько раз, по сравнению с однократным измерением? Мы их получим только тогда, когда откажемся от мысли завершить исследование на этапе расчета среднего значения измеряемой величины, сделав для этого традиционных 5-7 измерений. Многократные измерения нам нужны для того, чтобы опытным путем убедиться в том, что изучаемое явление может быть описано распределением Пуассона.

Как долго нужно проводить однократное измерение в серии многократных измерений? Настолько долго, чтобы его результаты в совокупности с результатами других измерений в данной серии позволили судить о применимости к данному исследованию свойств нормального распределения (смотри последовательность приведенных выше графиков: 10 секунд было мало, а 30 – вполне достаточно).

Сколько раз его необходимо повторить, чтобы использовать преимущества многократного метода? Чем больше экспериментальных точек мы имеем, тем надежнее наши выводы о свойствах изучаемых явлений, тем точнее мы можем выявить взаимосвязи между различными переменными, отразив их более плавными кривыми графически и более точными функциями аналитически. Однако, вместе с этой очевидной мыслью всегда следует помнить, что выбор метода исследования должен соотносится с условием конкретной исследовательской задачи. В авторском эксперименте было проведено 60 измерений. Подумайте, получим ли мы какие либо преимущества, если повторим опыт еще 10, 20, 40 или 60 раз? Ведь в каждом из них мы хаотически будем получать значения, лежащие в интервале (4-19) с вероятностью около единицы, и в интервале (6-12) с вероятностью 0,7. Нет оснований предполагать, что мы получим существенно отличающееся от девяти и среднее значение числа отсчитываемых частиц. Можно ли было провести измерений меньше, чем 60? Ответить на этот вопрос, мы предлагаем самостоятельно любому желающему, путем исключения из анализа, например, данных первой таблицы. Можно в первой таблице выбрать случайным образом несколько результатов и анализировать их, как бы в отсутствие всех остальных.

Давайте теперь представим, что мы работаем на экспериментальной установке, свойства которой уже были исследованы, и они описываются распределением Пуассона. Напомним, наша задача, как правило, определение скорости счета частиц. Именно от нее начинаются все другие задачи. Посмотрите на последнее из приведенных соотношений:

ε (V_ср)_% = 100/√ N

Относительная погрешность измерения скорости счета частиц обратно пропорциональна количеству зарегистрированных частиц. Для измерений с точностью до одного процента необходимо зарегистрировать 10 000 частиц, для точности 3% достаточно 1000 отсчетов, при точности 10% нужно всего 100 отсчетов.

Вывод: Если экспериментальная установка (радиоактивный препарат и счетчик числа частиц) заведомо может быть охарактеризована распределением Пуассона, то измерение числа частиц необходимо провести один (!) раз, выбрав такое время счета, чтобы было зарегистрировано не менее 100 частиц.