
- •Занятие 1 по MathCad
- •Ввод формул
- •Повторяющиеся вычисления
- •Форматирование результата
- •Матрицы и определители
- •Действия с векторами и матрицами
- •Транспортирование
- •Сложение (вычитание)
- •Умножение
- •О пределитель квадратной матрицы
- •Решение уравнений Решение одного уравнения
- •Решение систем линейных уравнений
- •Решение систем нелинейных уравнений и неравенств
Решение систем линейных уравнений
Система линейных алгебраических уравнений имеет вид:

Ее можно записать в матричной форме
![]() ,
где
,
где
![]() - матрица коэффициентов левой части
уравнений системы размерностью
- матрица коэффициентов левой части
уравнений системы размерностью
![]() ,
,
![]() - вектор неизвестных,
- вектор неизвестных,
![]() - вектор правых частей уравнений системы.
- вектор правых частей уравнений системы.
Система имеет единственное решение, если матрица А является невырожденной, т. е. ее определитель не равен нулю.
Пример. Решить систему линейных алгебраических уравнений:

Систему можно решать двумя способами.
Для решения системы записанной в матричной форме следует использовать встроенную функцию lsolve.
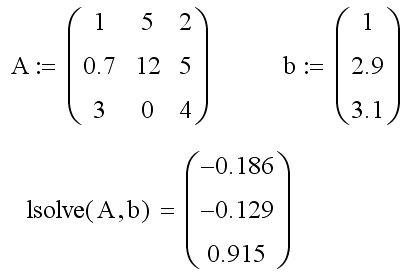
Если система записана в стандартном виде, для ее решения следует использовать вычислительный блок Given/Find.

Задать начальные приближения для всех неизвестных, входящих в систему уравнений (на основе начального приближения строится последовательность, сходящаяся к искомому решению).
Напечатать ключевое слово Given. Оно указывает, что далее следует система уравнений.
Ввести уравнения ниже ключевого слова.
Между левыми и правыми частями уравнений
должен стоять символ
![]() (жирный
знак равенства). Его можно взять из
панели Булевый или при нажатой
клавише Ctrl нажать
знак равенства.
(жирный
знак равенства). Его можно взять из
панели Булевый или при нажатой
клавише Ctrl нажать
знак равенства.
Записать функцию Find (перечислив в скобках неизвестные, входящие в систему) и нажать на клавишу «Равно». После знака равенства появится вектор корней уравнения.
Эту систему можно решить также с помощью определителей.

Задание. Решить разными
способами системы уравнений: и
и
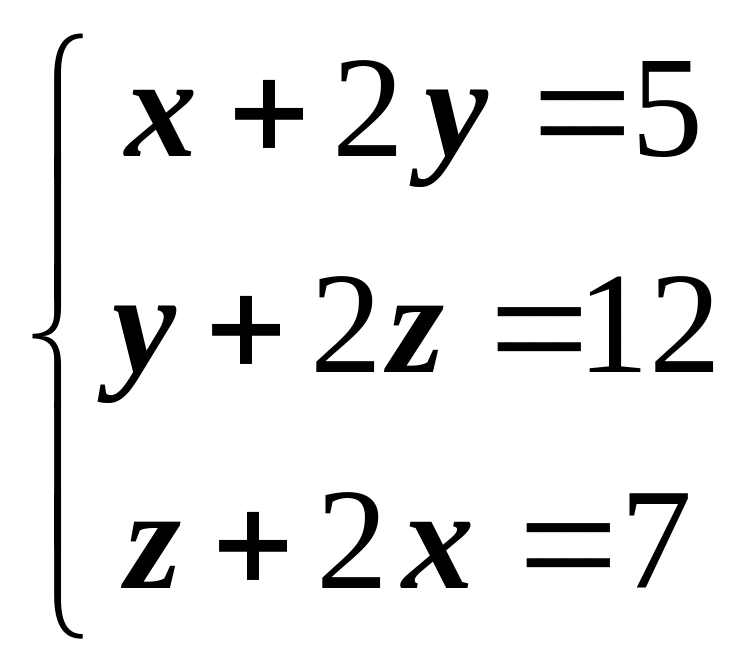 .
.
Решение систем нелинейных уравнений и неравенств
Для ее решения следует использовать вычислительный блок Given/Find. Действия аналогичны изложенным выше.
Между левыми и правыми частями неравенств может стоять любой из символов <, >, ≤ и ≥.
В качестве примера рассмотрим решение
системы уравненй:![]()
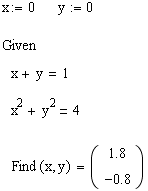

П ример
решения системы уравнений и неравенств.
ример
решения системы уравнений и неравенств.
Задание. Решить системы
уравнений:![]() и
и

