3.4 Поверхность вращения

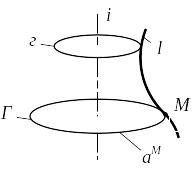
Поверхность вращения - поверхность, образованная вращением некоторой кривой (образующей) вокруг прямой (оси вращения).

 (i, l) [А: i - ось вращения; l - образующая; М  ; аM - окружность вращения точки М; Г  i - параллели

Рисунок 3.6

Параллель максимального радиуса вращения, если такая есть (у конуса ее нет) называется экватором.

Параллель минимального радиуса, если такая есть, называется горловой линией.

3.5 Цилиндрическая поверхность

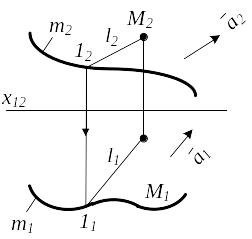
Цилиндрическая поверхность - линейчатая поверхность, образованная параллельным перемещением прямой (образующей) в пространстве, пересекающей кривую линию (направляющую).

 (a;m) А: - направление перемещения образующей; m - направляющая; М  ; l  M и l || l ∩ m

Рисунок 3.7

Цилиндрической поверхностью вращения называется поверхность, образованная вращением прямой линии параллельной оси вращения вокруг этой оси.

(i,l) [A] и ли (m,l)[A]

Рисунок 3.8

Цилиндром называется часть пространства, ограниченная замкнутой цилиндрической поверхностью и двумя плоскостями.

3.6 Коническая поверхность

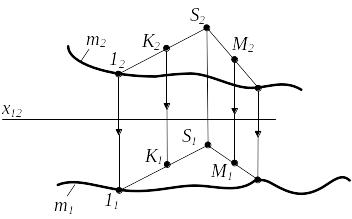
Конической - называется поверхность, образованная непрерывным перемещением прямой линии (образующей), проходящей через фиксированную точку и пересекающей кривую (направляющую).

(S,m)[A]

Рисунок 3.9

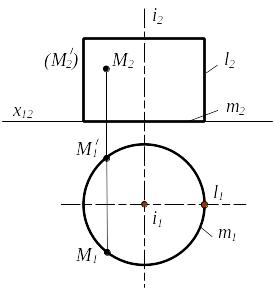
Коническая поверхность вращения - линейчатая поверхность, образованная вращением прямой (образующей) вокруг оси, пересекающей образующую в фиксированной точке (вершине конической поверхности).

Коническая поверхность вращения в пространстве и на чертеже задается своим определителем Ф (i, l)A, где

i ₁ - ось вращения; l - образующая; l  i  S - вершина;

M  Ф, M  a^M;

a^M - окружность вращения т.М;

R_M - радиус окружности вращения т.М, R_M = |O₁A₁| ;

M₂  M₁ (M′₁)

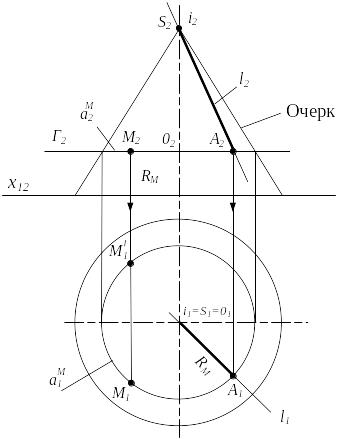
Рисунок 3.10

Через точку М построим параллель - окружность а. Окружность расположена в плоскости Г перпендикулярной оси вращения и параллельной П₁.

0А]  ₁ ; 0АR_M ; 0А0₁А₁

Т.к. точка М произвольная и построены ее проекции, достаточность геометрического определителя доказана.

Конусом называется часть пространства, ограниченная конической поверхностью, а также вершиной и плоскостью или двумя плоскостями.

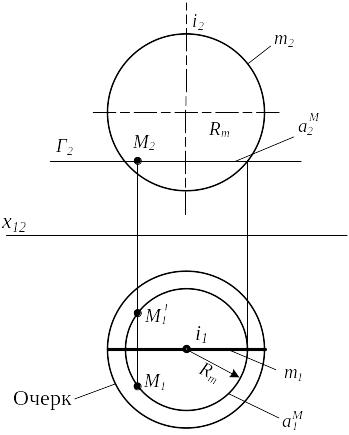
3.7 Сфера

Сфера - поверхность, состоящая из точек, равноотстоящих от фиксированной точки.

Если рассматривать сферу как тело вращения, то можно перезадать ее с помощью другого геометрического определителя: сфера - поверхность, образованная вращением окружности вокруг ее диаметра.

 (i; m)А: i - ось вращения; m – образующая; M  ; M  aM

Рисунок 3.11