3 Задание поверхностей на чертеже
3.1 Общие понятия
Поверхности могут быть заданы непрерывно (цилиндр, конус), а могут быть заданы дискретно линиями или точками.
Поверхность называется алгебраической, если соответствующее ей уравнение является алгебраическим многочленом.
Порядком поверхности с алгебраической точки зрения является наивысшая степень соответствующего ей алгебраического уравнения.
Порядком поверхности с геометрической точки зрения называется максимальное число точек пересечения произвольной прямой с этой поверхностью (включая мнимые точки).
Кинематические поверхности образуются непрерывным перемещением в пространстве некоторой линии - (образующей) по определенному закону.
Поверхность образованная перемещением прямой линии называется линейчатой.
Закон перемещения образующей определяется направляющими, максимальное количество которых может быть три. Направляющие могут вырождаться в точку, прямую, в плоскость параллелизма.
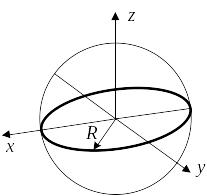
Уравнение сферы: x2 +y2 + z2 = R2 Поверхность второго порядка: N = 2 |
|
Рисунок 3.1
Определитель поверхности Ф(Г)А - в геометрической части совокупность проекций постоянных геометрических элементов и алгоритм построения точек линий поверхности.
А - алгоритмическая часть одинакова для всех поверхностей: точка принадлежит поверхности, если она принадлежит некоторой линии принадлежащей этой поверхности.
Поверхность считается заданной, если относительно любой точки пространства можно однозначно решить вопрос о принадлежности точки этой поверхности.
На комплексном чертеже поверхности задаются проекциями своего геометрического определителя, а изображаются своим очерком, т.е. проекциями линии контура и линии обреза.
3.2 Призматическая поверхность
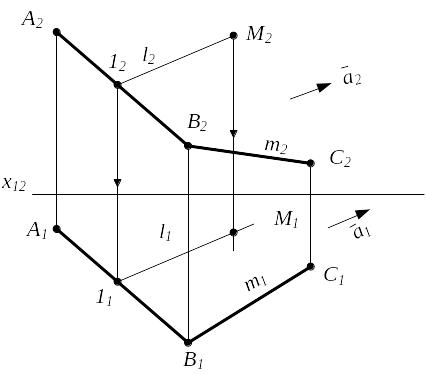
Призматическая поверхность - линейчатая поверхность, образованная параллельным перемещением прямой в пространстве (образующей) и пересекающей ломаную линию (направляющую).
Призматическая
поверхность в пространстве и на чертеже
задается своим определителем Ф
(m;
)А
где m - направляющая;
- направление перемещения образующей;
М Ф - произвольная точка, принадлежащая поверхности призмы;
l || - образующая, проходящая через т.М;
l М и l ∩ m = 1 М2 задана произвольно М 2 l2 l2 || ā2 l2 ∩ m2 = 12 12 11 и 11 l1 l1 || ā1 М1 l1 |
|
Рисунок 3.2
Т.к. М произвольная точка и вторая проекция ее построена, то теорема доказана.
Призма - геометрическая фигура, ограниченная замкнутой призматической поверхностью и двумя плоскостями.
l
Г
П1
|
|
П1
||
П1
Рисунок 3.3
3.3 Пирамидальная поверхность
Пирамидальная поверхность - поверхность образованная непрерывным перемещением прямой, проходящей через фиксированную точку и пересекающей ломаную линию.
Пирамидальная поверхность задается в пространстве и на чертеже своим определителем Ф(S,m)А, где S - вершина пирамиды; m – направляющая, ломаная линия.
Пирамидальная поверхность располагается по обе стороны от ее вершины, может быть замкнутой и незамкнутой.
М – произвольная точка, принадлежащая поверхности пирамиды.
Образующая l проходит через т.М, вершину S и пересекает направляющую m.
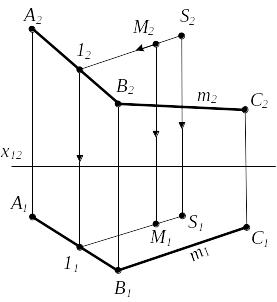
Рисунок 3.4
Пирамидой называется часть пространства, ограниченная пирамидальной поверхностью, а также вершиной и плоскостью или двумя плоскостями.
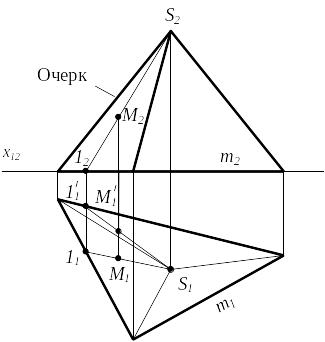
Рисунок 3.5