- •Конспект лекций
- •Инженерная и компьютерная графика
- •Содержание
- •1 Основы инженерной графики
- •1.1 Основные разделы инженерной графики
- •1.2 Свойства проецирования
- •1.3 Способы получения обратимого чертежа
- •2) Аксонометрические проекции.
- •1.4 Присоединение системы координат к системе плоскостей проекций
- •Вопросы для самоконтроля:
- •2 Задание основных элементов на чертеже
- •2.1 Определитель основных геометрических элементов и фигур
- •2.2 Прямая. Задание прямой линии на чертеже
- •2.3 Задание плоскости на чертеже
- •2.4 Классификация прямых и плоскостей
- •2.5 Взаимное расположение прямых
- •2.6 Взаимное расположение прямых и плоскостей
- •3 Задание поверхностей на чертеже
- •3.1 Общие понятия
- •3.2 Призматическая поверхность
- •3.3 Пирамидальная поверхность
- •3.4 Поверхность вращения
- •3.5 Цилиндрическая поверхность
- •3.6 Коническая поверхность
- •3.7 Сфера
- •3.8 Поверхности второго порядка:
- •Вопросы для самоконтроля:
- •4 Преобразование чертежа
- •4.1 Способ замены плоскостей проекций
- •4.2 Основные задачи, решаемые заменой плоскостей проекций
- •4.3 Способ вращения
- •Вопросы для самоконтроля:
- •5 Метрические задачи
- •6 Позиционные задачи
- •6.1 Классификация позиционных задач
- •6.2 Взаимное пересечение двух плоскостей (1 группа позиционных задач)
- •6.3 Взаимное пересечение прямой и плоскости или поверхности (2 группа позиционных задач)
- •6.4 Взаимное пересечение плоскости и поверхности (3 группа позиционных задач)
- •6.5 Взаимное пересечение поверхностей (4 группа позиционных задач)
- •Вопросы для самоконтроля:
- •7 Виды, разрезы, сечения
- •Вопросы для самоконтроля:
- •8 Правила нанесения размеров на чертежах
- •8.1 Общие положения
- •8.2 Размерные и выносные линии. Размерные числа
- •8.3 Условные знаки и упрощенное нанесение размеров
- •Вопросы для самоконтроля:
- •9. Шероховатость поверхности и ее обозначение на чертежах
- •9.1 Основные положения, термины и определения
- •9.2 Параметры шероховатости поверхности
- •9.3 Рекомендации по выбору параметров шероховатости на учебных чертежах и эскизах деталей
- •9.4 Обозначения шероховатости поверхности на чертежах
- •Вопросы для самоконтроля:
- •10. Компьютерная графика
- •10.1 Интерактивная машинная графика.
- •10.2 Средства работы с компьютерной графикой
- •10.3 Стандарт машинной графики gks (гкс, ягс)
- •10.4 Растровая графика
- •Достоинства растровой графики:
- •10.5 Векторная графика
- •Достоинства векторной графики:
- •10.6 Цвет в машинной графике
- •10.7 Разрешающая способность
- •10.7.1 Разрешающая способность битовой глубины
- •10.7.2 Разрешающая способность графического изображения
- •10.7.3 Разрешающая способность устройства ввода
- •10.7.4 Разрешающая способность монитора
- •10.8 Преобразование форматов графических файлов
2.5 Взаимное расположение прямых
1) Прямые параллельны
|
|
Рисунок 2.12
Если две прямые в пространстве параллельны, то и соответствующие проекции этих прямых параллельны и обратно, если соответствующие проекции двух прямых параллельны, и прямые в пространстве параллельны.
Чтобы прямые в пространстве были параллельны, необходимо и достаточно, чтобы соответствующие проекции прямых были параллельны (или совпадали).
2) Прямые пересекаются а∩b=М а1 ∩ b1 М1 ; а2 ∩ b2 М2
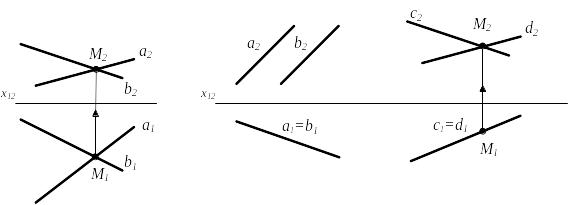
а) ab б) a || b в) c∩d
Рисунок 2.13
Если две прямые, параллельные или пересекающиеся, лежат в одной проецирующей плоскости, их изображения на соответствующую плоскость проекций совпадут. Такие прямые называются конкурирующими (рис. 2.13б,в) – конкурирующие относительно пл. П1.
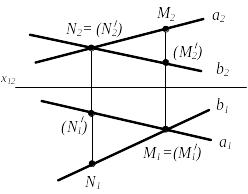
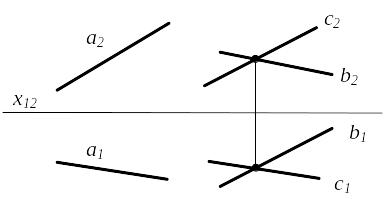
3) Прямые скрещивающиеся аb а1 ∩ b1 М1 ; а2 ∩ b2 N2
|
М и М′ - конкурирующие точки относительно плоскости П1
N и N′ - конкурирующие точки относительно плоскости П2 |
Рисунок 2.14
2.6 Взаимное расположение прямых и плоскостей
1) Прямая параллельна плоскости
a || (b ∩ c), если a 1 || c1 a2 || c2 |
|
Рисунок 2.15
Прямая параллельна плоскости, если она параллельна хотя бы одной прямой, принадлежащей этой плоскости.
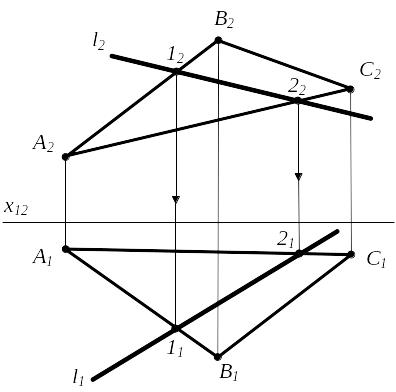
2) Прямая принадлежит плоскости
l (ABC)
l (1,2)
(1,2) (ABC)
1 AB (11 A1B1; 12 A2B2)
2 AC (21 A1C1; 22 A2C2)
|
|
Рисунок 2.15
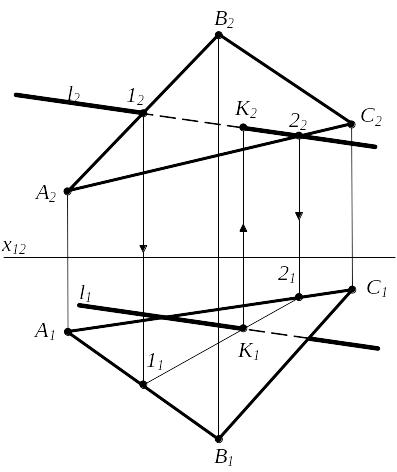
3) Прямая пересекает плоскость (первая основная позиционная задача)
l ∩ (ABC) =K, т.к.
l и (1,2) конкурирующие прямые и
(1,2) (ABC), а
l ∩ (1,2) = K Для определения видимости необходимо рассмотреть расположение конкурирующих точек l и АВ относительно П2; l и ВС относительно П1
|
|
Рисунок 2.16
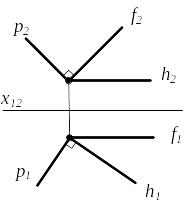
4) Прямая перпендикулярна плоскости
p ( f ∩ h)
p1 h1
p2 f2
|
|
Рисунок 2.17
Прямая перпендикулярна плоскости, если она перпендикулярна каким-нибудь двум пересекающимся прямым этой плоскости.
Т.к. прямой угол проецируется прямым, если одна из его сторон параллельна плоскости проекций, для построения перпендикуляра к плоскости целесообразно взять в качестве пересекающихся прямых прямые уровня плоскости фронталь и горизонталь.
Следовательно, если прямая перпендикулярна к плоскости, то горизонтальная проекция прямой перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали.
Чтобы прямая в пространстве была перпендикулярна плоскости, необходимо и достаточно, чтобы ее проекции были перпендикулярны соответствующим проекциям фронтали и горизонтали плоскости (там, где мы их видим в натуральную величину, т.е. перпендикулярны f и h).
5) Параллельные плоскости
Если две плоскости в пространстве параллельны, то соответствующие проекции двух пересекающихся прямых одной плоскости должны быть параллельны двум проекциям пересекающихся прямых другой плоскости и наоборот.
Если соответствующие проекции двух пересекающихся прямых одной плоскости параллельны проекциям двух пересекающихся прямых другой плоскости, то в пространстве им соответствуют параллельные плоскости.
(a ∩ b) || Г(c ∩ d)
a
b || c (b1 || d1 ; b2 || d2)
|
|
Рисунок 2.18
Чтобы плоскости в пространстве были параллельны необходимо и достаточно, чтобы проекции двух пересекающихся прямых одной плоскости были параллельны соответствующим проекциям двух пересекающихся прямых другой плоскости.
Вопросы для самоконтроля:
1) Что является определителем геометрических фигур?
2) Что является геометрическим определителем прямой?
3) Что является геометрическим определителем плоскости?
4) Постройте чертеж произвольной точки К, принадлежащей плоскости (А,b) и (а∩b) на рисунке 2.2.
5) Приведите классификацию прямых и плоскостей относительно плоскостей проекций.
6) Дайте определение конкурирующим точкам и прямым.
7) Приведите примеры чертежей проецирующих прямых и плоскостей.
8) Приведите примеры чертежей прямых и плоскостей уровня.
9) Проведите в плоскостях общего положения, заданных на чертежах рисунка 2.2, горизонтали и фронтали.
10) Что называется следами прямой? Найти следы прямой l или АВ на рисунке 2.1.
11) Найдите длину отрезка АВ рисунок 2.1 по правилу прямоугольного треугольника.
12) Что называется следами плоскости? Задайте произвольную плоскость следами.
13) Приведите примеры чертежей всех вариантов взаимного расположения прямых в пространстве.
14) Приведите примеры чертежей всех вариантов взаимного расположения прямых и плоскостей в пространстве.
15) Постройте чертежи плоскостей, параллельных заданным на чертежах рисунка 2.2 (А,В,С), (А,b), (а∩b) и (а||b).
16) Постройте точки пересечения произвольной прямой l с плоск. и .

 а||b
а1
||
b1
; а2
|| b2
а||b
а1
||
b1
; а2
|| b2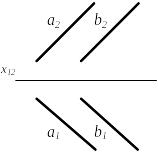


 || c
(a1
|| c1
; a2
|| c2)
|| c
(a1
|| c1
; a2
|| c2)