2.4 Классификация прямых и плоскостей

В зависимости от расположения прямых и плоскостей относительно плоскостей проекций все прямые и плоскости делят на прямые и плоскости общего положения и частного.

Прямые и плоскости перпендикулярные или параллельные плоскостям проекций называются прямыми и плоскостями частного положения.

Прямые и плоскости перпендикулярные плоскостям проекций -проецирующие прямые или плоскости.

У проецирующих прямых одна из проекций вырождается в точку, а у плоскостей в прямую.

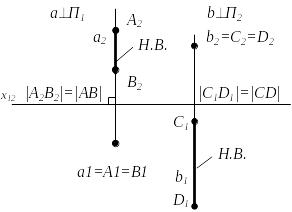
Прямые перпендикулярные горизонтальной плоскости проекций называются горизонтально проецирующими прямыми (рис.2.3, а).

Прямые перпендикулярные фронтальной плоскости проекций называются фронтально проецирующими прямыми (рис.2.3, б).

Точки, лежащие на одном проецирующем луче называются конкурирующими относительно соответствующей плоскости проекций (рис.2.3).

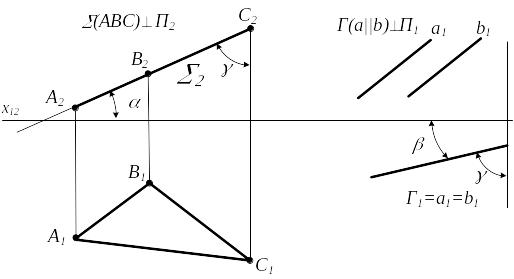
Плоскости перпендикулярные горизонтальной плоскости проекций называются горизонтально проецирующими плоскостями (рис.2.4, б).

Плоскости перпендикулярные фронтальной плоскости проекций называются фронтально проецирующими плоскостями (рис.2.4, а).

а) б) а) б)

Рисунок 2.3 Рисунок 2.4

Прямые, лежащие в одной проецирующей плоскости, называются конкурирующими прямыми, например, прямые а и в или АВ и ВС на рисунке 2.4.

На комплексном чертеже у проецирующих плоскостей сразу определяются углы наклона к плоскостям проекций , ,  (рис.2.4).

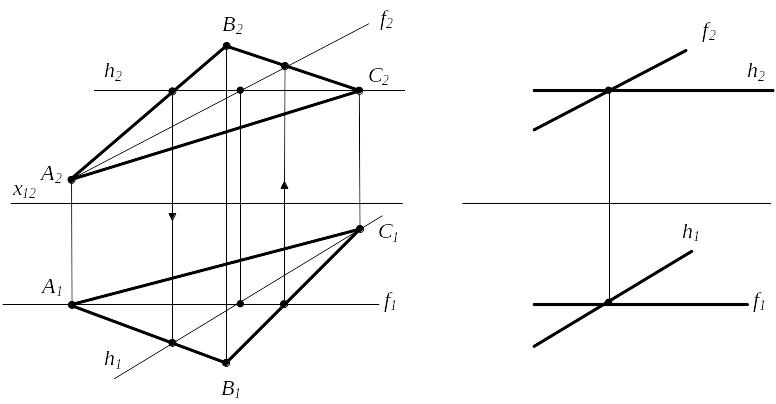
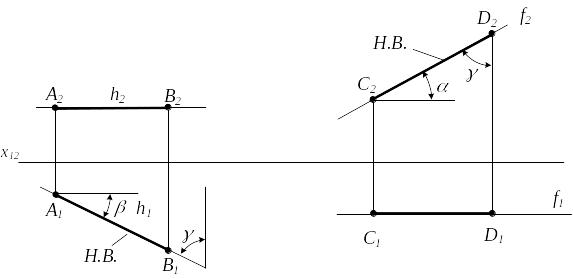
Прямые и плоскости параллельные плоскостям проекций - прямые и плоскости уровня. (рис. 2.5 и рис.2.6)

h – горизонталь h2 || x12 |A1B1| = |AB|	f – фронталь f2 || x12 |C2D2| = |CD|

а) б)

Рисунок 2.5 Прямые уровня

Прямая параллельная горизонтальной плоскости про­екций, называется горизонтальной прямой или горизонталью (рис. 2.5, а).

Прямая параллельная фронтальной плоскости проекций, называется фронтальной прямой или фронталью (рис. 2.5, б).

У прямых уровня на комплексном чертеже сразу определяются углы наклона к плоскостям проекций , ,  (рис.2.5).

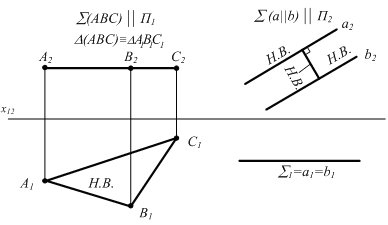
Плоскость параллельная горизонтальной плоскости про­екций, называется горизонтальной плоскостью (рис. 2.6, а).

Плоскость параллельная фронтальной плоскости проекций, называется фронтальной плоскостью (рис. 2.6, б).

а) б)

Рисунок 2.6 Плоскости уровня

Геометрические фигуры, лежащие в плоскостях уровня (параллельных плоскостям проекций) проецируются без искажения на плоскость проекций, которой они параллельны (рис.2.6).

Прямая или плоскость параллельная профильной плоскости проекций называется профильной прямой или плоскостью. Для построения чертежа профильной прямой необходимо использовать трехкартинный эпюр (рис.2.7).

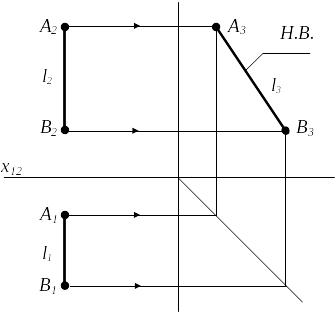
Рисунок 2.7

Прямая или плоскость общего положения - неперпендикулярная и непараллельная ни одной из плоскостей проекций.

Точки пересечения прямых с плоскостями проекций называются соответ­ственно горизонтальным (H) и фронтальным (F) следами прямых (рис.2.8).

Правило прямоугольного треугольника:

Длина отрезка прямой общего положения определяется гипотенузой прямоугольного треугольника, один катет которого является одна из проекций этого отрезка, а другой- алгебраическая разность расстояний от концов отрезка до соответствующей плоскости проекций.

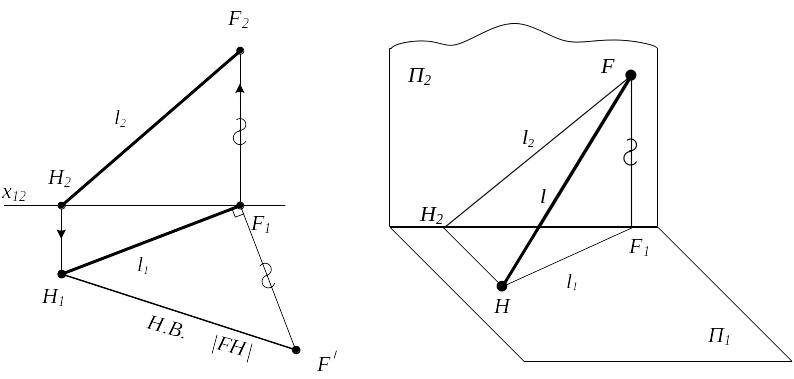
Рисунок 2.8

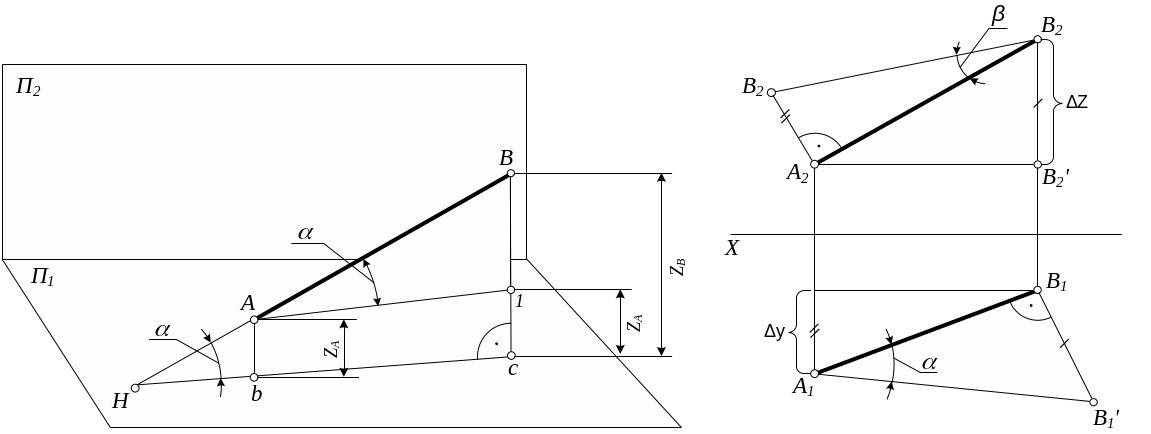
Рисунок 2.9

Линии пересечения плоскостей с плоскостями проекций называются соответственно горизонтальным и фронтальным следами плоскостей (рис.2.10).

Три плоскости П₁, П₂ и  пересекаются в одной точке схода следов.

Задание плоскости следами - это частный способ ее задания, разновидность задания плоскости двумя пересекающимися прямыми  f ∩ h.

Рисунок 2.10

В любой заданной плоскости всегда можно провести сколько угодно главных линий плоскости - горизонталей и фронталей (рис.2.10). Все горизонтали (фронтали), лежащие в одной плоскости, параллельны между собой.

f  (ABC) f 1 || x12 h  (ABC) h2 || x12

Рисунок 2.11