1.3 Способы получения обратимого чертежа

Недостатком ортогонального проецирования на одну плоскость проекций является необратимость чертежа.

Чертеж называется обратимым, если он определяет оригинал однозначно, как по форме, так и по положению в пространстве относительно заданной системы координат.

Чертеж из одного изображения оригинала является необратимым. Для исключения неопределенности существует несколько способов получения обратимых чертежей.

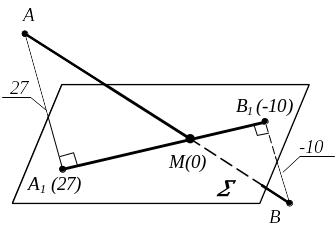
1) Проекции с числовыми отметками (используется в топографии, картографии) (рис. 1.4).

А  А1 А 1 (27) В1 (-10)

Рисунок 1.4

2) Аксонометрические проекции.

Аксонометрия - проекция оригинала на плоскость вместе с жестко связанной с ним системой координат.

Координаты точки А - это коэффициенты разложения радиуса - вектора точки А по единичным векторам (ортам) (рис.1.5).

Существует основная теорема аксонометрии, доказывающая, что

Любые три луча, выходящие из одной точки и лежащие в одной плоскости проекций можно принять за проекции заданной системы координат с равными масштабными единицами на них.

Аксонометрический чертеж является обратимым чертежом.

Используя свойство сохранения пропорциональности отрезков при ортогональном проецировании, можно перейти к натуральной системе координат, следовательно, чертеж обратим.

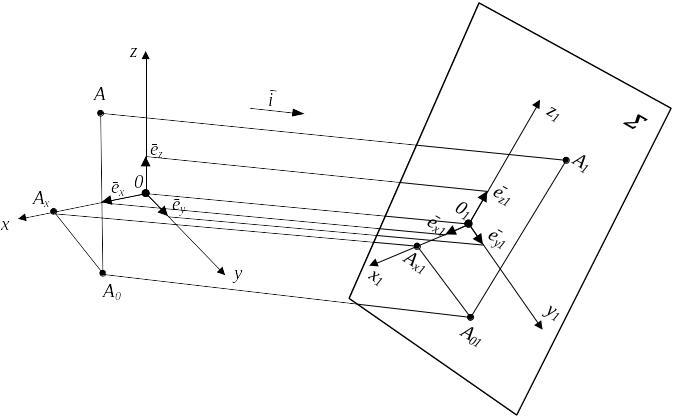
 - плоскость аксонометрических проекций;

- вектор, определяющий параллельное проецирование;

0 - аксонометрическое начало;

x, y, z - аксонометрические оси;

- аксонометрические единичные векторы;

А₁ - проекция точки А

Рисунок 1.5

Примечание: на аксонометрическом чертеже обязательно кроме проекции А₁ должна быть задана и одна из проекций точки А в системе координат А₁  А₀₁ .

Отношение длины проекции аксонометрического единичного вектора к его натуральной длине называется коэффициентом искажения по соответствующей оси.

Коэффициенты искажения длины отрезка по аксонометрическим осям могут принимать различные значения:

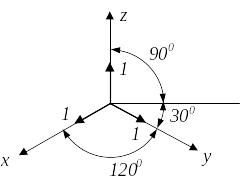
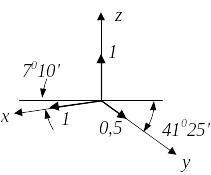
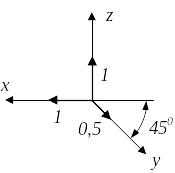
На практике используется три частных случая аксонометрических проекций: изометрия (mnp0,82), диметрия (mp0,94; n 0,5m) и косоугольная диметрия (mp1; n0,5).

Для упрощения в ЕСКД (единой системе конструкторской документации) приняты стандартные аксонометрические проекции со следующими значениями коэффициентов искажения и расположения осей:

Изометрия Mnp1	Диметрия mp1; n0,5	Косоугольная диметрия mp1; n0,5

Рисунок 1.6

3) Комплексный чертеж или эпюр Монжа (основной способ начертательной геометрии предложенный французским ученым Гаспаром Монжем)

Комплексный чертеж - чертеж, получаемый ортогональным проецированием на две взаимно перпендикулярные плоскости проекций. В пространстве фиксируются две взаимно перпендикулярные плоскости проекций: П1₂

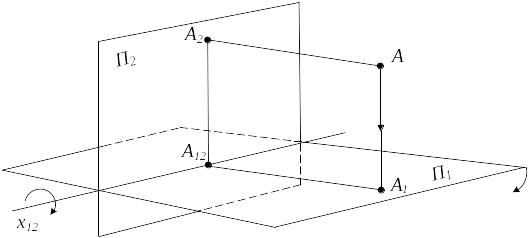
₁ - горизонтальная плоскость проекций;

₂ - фронтальная плоскость проекций;

x₁₂ - линия пересечения плоскостей проекций, ось чертежа;

А - оригинал;

А₁ - горизонтальная проекция точки А;

А₂ - фронтальная проекция точки А.

Рисунок 1.7

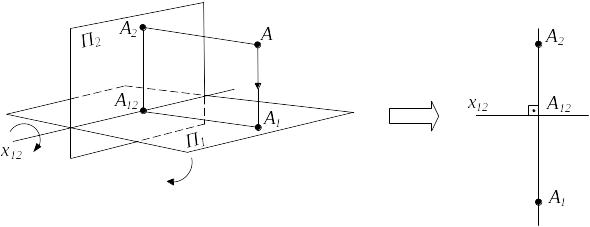
А₁ А₂ - линия связи; А₁ А₂  x₁₂

Рисунок 1.8

Гаспар Монж предложил зафиксировать плоскость ₂, а ₁ вращать вокруг оси x до совмещения с пл. ₂. От оригинала отказываемся. Линия, соединяющая обе проек­ции на чертеже, называется линией связи. Она всегда перпендикулярна оси чертежа.

Одновременное проецирование на две взаимно перпендикулярные плоскости проекций позволяет получить обратимый чертеж. Комплексный чертеж является чертежом обратимым.

АА₁|А₂ А₁₂ (А₁) - расстояние от т. А до плоскости ₁ – высота.

АА₂А₁А₁₂ (А₂) - расстояние от т. А до плоскости ₂ – глубина.

Таким образом, по чертежу можно определить расстояния от точки А до плоскостей проекций, что говорит об обратимости комплексного чертежа.

Две проекции точки А₁ и А₂ на линии связи (А₁А₂ )x₁₂ задают единственную точку А в пространстве.

Заданные плоскости проекций делят пространство условно на четыре чет­верти (или квадранта).

Т.к. плоскости проекций относительно объекта мы задаем сами, то удобнее всего оригинал (объект) располагать в первой четверти: над горизонтальной плоскостью проекций и перед фронтальной плоскостью проекций. Однако надо иметь в виду, что при решении конкретных задач прямые, плоскости или поверхности могут уйти за пределы первой четверти, во вторую, третью или четвертую четверти.

Рисунок 1.9