- •Конспект лекций
- •Инженерная и компьютерная графика
- •Содержание
- •1 Основы инженерной графики
- •1.1 Основные разделы инженерной графики
- •1.2 Свойства проецирования
- •1.3 Способы получения обратимого чертежа
- •2) Аксонометрические проекции.
- •1.4 Присоединение системы координат к системе плоскостей проекций
- •Вопросы для самоконтроля:
- •2 Задание основных элементов на чертеже
- •2.1 Определитель основных геометрических элементов и фигур
- •2.2 Прямая. Задание прямой линии на чертеже
- •2.3 Задание плоскости на чертеже
- •2.4 Классификация прямых и плоскостей
- •2.5 Взаимное расположение прямых
- •2.6 Взаимное расположение прямых и плоскостей
- •3 Задание поверхностей на чертеже
- •3.1 Общие понятия
- •3.2 Призматическая поверхность
- •3.3 Пирамидальная поверхность
- •3.4 Поверхность вращения
- •3.5 Цилиндрическая поверхность
- •3.6 Коническая поверхность
- •3.7 Сфера
- •3.8 Поверхности второго порядка:
- •Вопросы для самоконтроля:
- •4 Преобразование чертежа
- •4.1 Способ замены плоскостей проекций
- •4.2 Основные задачи, решаемые заменой плоскостей проекций
- •4.3 Способ вращения
- •Вопросы для самоконтроля:
- •5 Метрические задачи
- •6 Позиционные задачи
- •6.1 Классификация позиционных задач
- •6.2 Взаимное пересечение двух плоскостей (1 группа позиционных задач)
- •6.3 Взаимное пересечение прямой и плоскости или поверхности (2 группа позиционных задач)
- •6.4 Взаимное пересечение плоскости и поверхности (3 группа позиционных задач)
- •6.5 Взаимное пересечение поверхностей (4 группа позиционных задач)
- •Вопросы для самоконтроля:
- •7 Виды, разрезы, сечения
- •Вопросы для самоконтроля:
- •8 Правила нанесения размеров на чертежах
- •8.1 Общие положения
- •8.2 Размерные и выносные линии. Размерные числа
- •8.3 Условные знаки и упрощенное нанесение размеров
- •Вопросы для самоконтроля:
- •9. Шероховатость поверхности и ее обозначение на чертежах
- •9.1 Основные положения, термины и определения
- •9.2 Параметры шероховатости поверхности
- •9.3 Рекомендации по выбору параметров шероховатости на учебных чертежах и эскизах деталей
- •9.4 Обозначения шероховатости поверхности на чертежах
- •Вопросы для самоконтроля:
- •10. Компьютерная графика
- •10.1 Интерактивная машинная графика.
- •10.2 Средства работы с компьютерной графикой
- •10.3 Стандарт машинной графики gks (гкс, ягс)
- •10.4 Растровая графика
- •Достоинства растровой графики:
- •10.5 Векторная графика
- •Достоинства векторной графики:
- •10.6 Цвет в машинной графике
- •10.7 Разрешающая способность
- •10.7.1 Разрешающая способность битовой глубины
- •10.7.2 Разрешающая способность графического изображения
- •10.7.3 Разрешающая способность устройства ввода
- •10.7.4 Разрешающая способность монитора
- •10.8 Преобразование форматов графических файлов
6.3 Взаимное пересечение прямой и плоскости или поверхности (2 группа позиционных задач)
а М
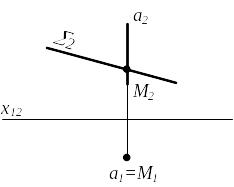
Вариант А. Прямая и плоскость являются проецирующими
а 1 2 М а; а1; М1 а1; М ; 2 ; М2 а22
|
|
Рисунок 6.5
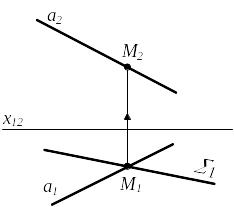
Вариант В-1. Прямая общего положения пересекается с проецирующей плоскостью
а 1 а = М Ма, М, 1 М1 а11; Ма М2а2
|
|
Рисунок 6.6
Вариант В-2. Проецирующая прямая пересекается с плоскостью общего положения
а 1; (с || d) – общего положения. М а ; М1 = а1 М , поэтому через т. М проводим произвольную прямую l в плоскости 11 = l1 с1; 21= l1 d1 M1 l1(11,21) ; l l(1;2) M1 l1(11;21); М2 l2(12,22) или l2 a2 = М2 Для определения видимости на 2 рассмотрим конкурирующие точки 3 с и 4 а. Т.к. точка 3 к нам ближе на плоскости 2 мы видим ее. |
|
Рисунок 6.7
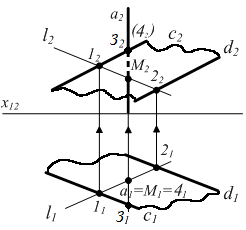
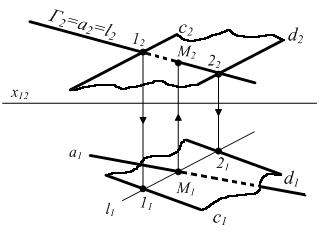
Вариант С. Прямая и плоскость общего положения
Не рационально использовать замену плоскостей проекций. Задача решается по общему алгоритму:
1) Вводим вспомогательную секущую плоскость Г через прямую а. Вспомогательная плоскость всегда вводится проецирующей: Г1 (или 2) и обязательно Г а.
2) Находим линию пересечения Г с : Г l (1;2).
Это 1 группа задач варианта В рассмотрена выше.
3) l (1;2) и прямая а лежат в одной плоскости Г; l а M - искомая точка пересечения прямой а и плоскости .
Рассмотрим задачу.
а – общего положения; (c || d) – общего положения. а М 1 ) Г2 и а 2) Г l (1,2) 1 Гc 2 Гd 3) lа M (l1 а1 M1 ; М2 а2) 4) Для определения видимости необходимо рассмотреть конкурирующте точки прямой а и c или d. |
|
Рисунок 6.8
6.4 Взаимное пересечение плоскости и поверхности (3 группа позиционных задач)
В сечении поверхности плоскостью получается плоская фигура, которую строят по точкам. При этом начинают построение с опорных точек - точек, лежащих на линиях контура, ребрах и линиях основания поверхности.
Если проекция линии пересечения этими точками не определяется полностью, то строят дополнительные промежуточные точки. Чертеж всегда можно преобразовать заменой плоскостей проекций так, чтобы секущая плоскость стала проецирующей.
Поэтому начнем рассматривать случаи пересечения поверхности и плоскости частного положения.
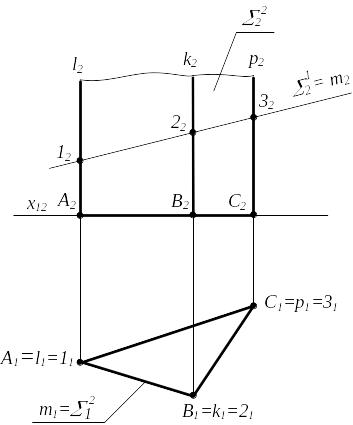
Вариант А-1. Плоскость и поверхность являются проецирующими к разным плоскостям проекций
12 ; 21 - призма 1 2 m ; 12 m2 = 12
1 2 k 1 3 p 1 m2 (122232) m1 (112131) = 21
|
|
Рисунок 6.9
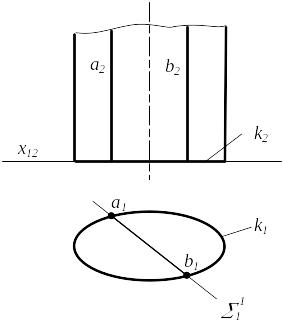
Вариант А-2. Плоскость и поверхность являются проецирующими относительно одной плоскости проекций
1 - плоскость 2 - поверхность 1 2 m 1 1 2 1 - цилиндр 1 2 a,b
|
|
Рисунок 6.10
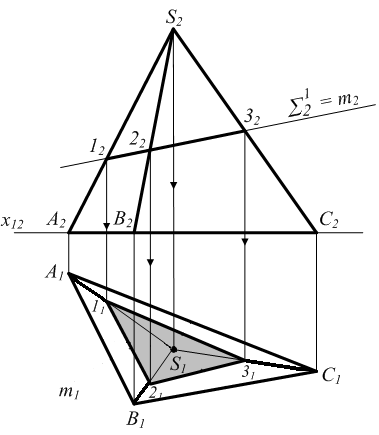
Вариант В-1. Плоскость проецирующая пересекается с поверхностью общего положения
12 ; 2 - пирамида 1 2 m 1 1 (SA) 2 1 (SB) 3 1 (SC) m2 (122232) m1 (112131) - по принадлежности m поверхности 2 - пирамиды
|
|
Рисунок 6.11
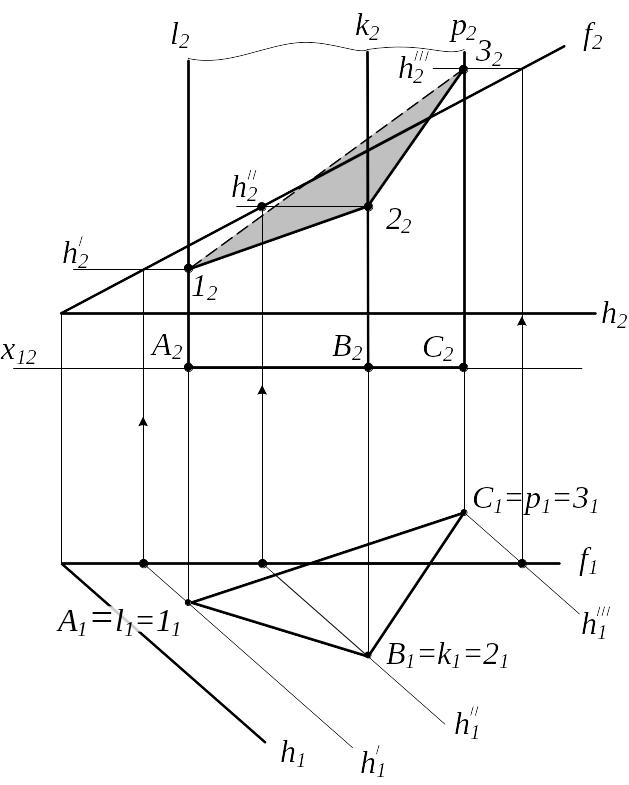
Вариант В-2. Плоскость общего положения пересекается с проецирующей поверхностью
1 (f h) – общего положения. 2 1 - призма 1 2 m (1;2;3) 1 l 1 ; l1 11 2 k 1 ; k1 21 3 p 1 ; p1 31 m1 (112131). Точки сечения 1,2,3 находятся по принадлежности плоскости (fh). 11 h′1 ; h′ h′1 h1 ; 12 h′2 Аналогично определяются фронтальные проекции т.2 и 3 m2 (12;22;32), m 1;2;3 |
|
Рисунок 6.12
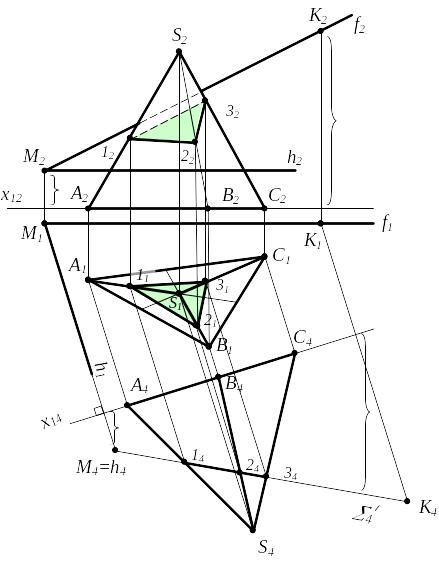
Вариант С. Плоскость и поверхность общего положения
Целесообразно заменой плоскостей проекций привести к варианту В-1
1 (f h); 2 - пирамида; 1 2 m(1;2;3) 2 41x14h11 1 1 (SA) 2 1 (SB) 3 1 (SC) m4 14,24,34 m2; m1(11,21,31) и m2(12,22,32)
|
|
Рисунок 6.13
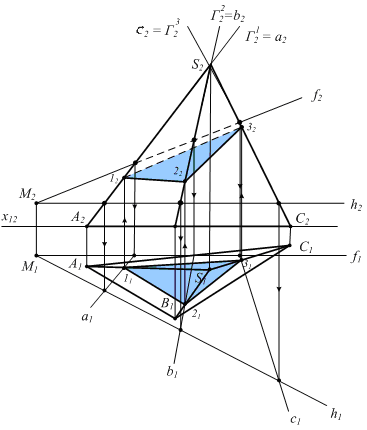
Рассмотрим решение этой же задачи по общему алгоритму. Вводим вспомогательные плоскости через ребра пирамиды.
1) Г1SA ; 12 2) 11 a ; (12 a2) a2f2 ; a2h2 3 ) a (SA) 1 (a1S1A1) Вводим пл. Г2 1) Г2 SB; Г22 2) Г2 1 b ; (22 b2) b2f2 ; b2h2 3) b (SB) 2 ; (b1S1B1) Вводим пл. Г3 через ребро SC и повторяем алгоритм, находим т.3.
|
|
Рисунок 6.14
При пересечении криволинейных поверхностей или поверхностей вращения плоскостью вспомогательные плоскости вводятся через образующие поверхностей или перпендикулярно оси вращения. Найденные точки соединяются по лекалу.
В сечении цилиндрической поверхности вращения плоскостью могут быть получены следующие линии:
окружность, если секущая плоскость перпендикулярна оси вращения цилиндрической поверхности;
эллипс, если секущая плоскость не перпендикулярна и не параллельна оси вращения;
две образующие прямые, если секущая плоскость параллельна оси вращения.
В сечении конической поверхности вращения плоскостью могут быть получены следующие линии:
окружность, если секущая плоскость перпендикулярна оси вращения;
эллипс, если секущая плоскость пересекает все образующие;
парабола, если секущая плоскость параллельна только одной образующей;
гипербола, если секущая плоскость параллельна двум образующим;
две образующие прямые, если секущая плоскость проходит через вершину.
В сечении сферы плоскостью всегда получается окружность.

 – общего положения;
– общего положения;

l
1
l
1