6 Позиционные задачи

6.1 Классификация позиционных задач

Позиционные задачи в начертательной геометрии связаны с решением на комплексном чертеже вопросов взаимного расположения геометрических объектов: задачи на принадлежность и задачи на взаимное пересечение.

Задачи на принадлежность решаются с помощью алгоритмической части при­надлежности точек плоскости или поверхности.

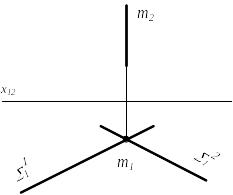
Задачи на взаимное пересечение можно разделить на две части: 1, 3 и 4 группы - взаимное пересечение поверхностей и плоскостей и 2 группа - пересечение прямой и поверхности (плоскости) (рис. 6.1.).

Решение всех задач начинается с анализа расположения геометрических объектов относительно плоскостей проекций.

Возможно три варианта сочетания элементов:

А - оба геометрических объекта занимают проецирующее положение;

В - один из элементов проецирующий, а второй общего положения;

С - оба объекта занимают общее положение.

Для варианта А - на чертеже имеются обе проекции искомого геометрического объекта.

Для варианта В - на чертеже имеется одна соответствующая проекция искомого геометрического элемента, а вторая проекция ищется по принадлежности искомого элемента исходному объекту общего положения задачи.

Для варианта С - если возможно, методом замены плоскостей проекций перейти к варианту В. В общем случае задачи решаются по следующему алгоритму:

1) Вводится вспомогательная секущая плоскость или поверхность (одна, две или несколько, в зависимости от условия задач).

2) Находятся линии пересечения вспомогательной плоскости или поверхности с каждым из данных объектов.

3) Находятся точки пересечения этих линий.

4) Определяется видимость.

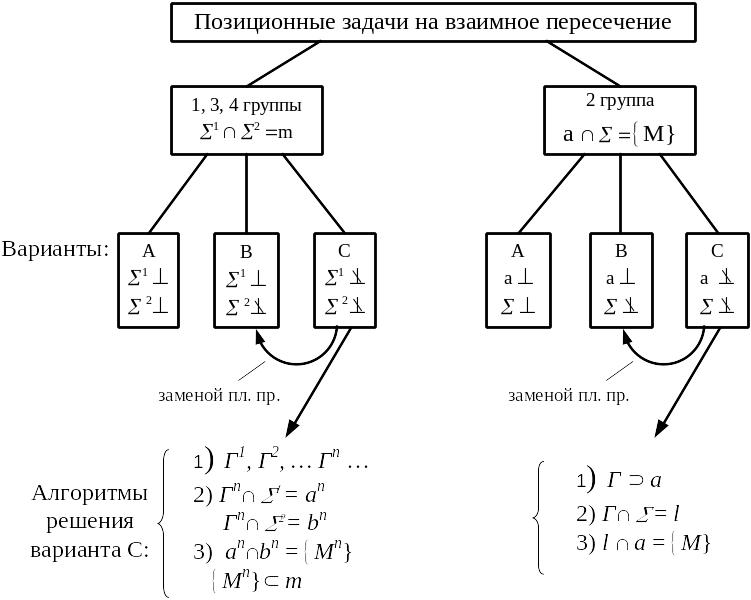
Рисунок 6.1 Классификация позиционных задач на взаимное пересечение

6.2 Взаимное пересечение двух плоскостей (1 группа позиционных задач)

Для построения линии пересечения двух плоскостей необходимо найти две точки этой линии:

¹ ²  m (1;2)

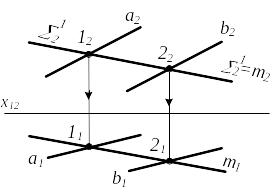
Вариант А. Обе плоскости проецирующие (рис.6.2)

а) ¹₁ или б) ¹₁

²₁ ²₂

Т.к. m¹ и ², то единственное решение- пересечение этих плоскостей:

¹₁ ²₁  m₁: для случая (а) m₁, если плоскости не параллельны; для случая (б) m₁  ¹₁ , m₂  ²₂

а)	б)

Рисунок 6.2

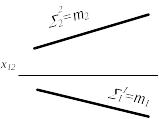
Вариант В. Одна из плоскостей проецирующая

Если одна из плоскостей занимает частное положение, то ее вырожденная в прямую проекция включает в себя и проекцию линии пересечения плоскостей.

12 2(a||b) - плоскость общего положения 1 2 m (1;2)  m  1, 2 m2  12 но m  2, следовательно: m  a  (1), mb  (2) или m2a2  (12); m2b2  (22)  m2(12;22), а m1(11;21) определяется по принадлежности

Рисунок 6.3

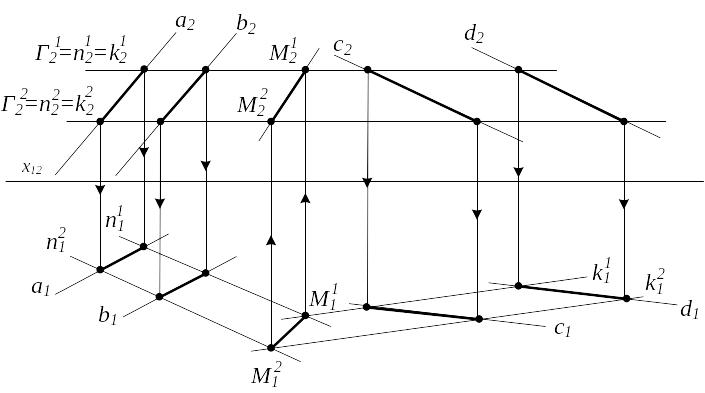
Вариант C. Обе плоскости общего положения

Для решения таких задач возможны два пути решения: по общему алгоритму или методом замены плоскостей проекций. Задача слишком проста для решения громоздким методом замены плоскостей проекций, поэтому решаем по общему алгоритму.

1) Вводим вспомогательную секущую плоскость Г¹. Вспомогательные плоскости всегда вводятся проецирующими: Г¹₂ (или ₁).

2) Находим линии пересечения Г¹ с ¹ и ² ; Г¹  ¹ n¹; Г¹  ²  k¹.

(Это группа задач варианта В рассмотрена выше).

3) т.к. n¹ и k¹ лежат в одной плоскости Г¹, то n¹  k¹  M¹ - точка пересечения плоскостей ¹ и ².

Алгоритм решения повторяется: вводя вторую вспомогательную секущую плоскость Г² находим точку М². ¹  ²  m (М¹; М²).

Рассмотрим задачу.

1 (a || b) – общего положения 2 (c || d) – общего положения
1) Г12 2) Г11  n1 Г12  k1 3) n1  k1  M1 M1m	1) Г2 2) Г21  n2 Г22  k2 3) n2k2  M2 M2m

Рисунок 6.4