4.2 Основные задачи, решаемые заменой плоскостей проекций

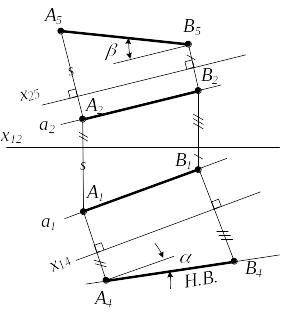
Задача 1. Прямую общего положения преобразовать в прямую уровня (параллельную плоскости проекций).

Алгоритм преобразования (рис.4.5):

1. П₄||a или П₅||a

2.  - проецирование ортогонально новой плоскости проекций;

3.  - const - сохранение расстояний.

Т.к. а||П₄ или ||П₅ , то длина отрезка АВ может быть найдена по чертежу:

|АВ||А₄В₄|А₅В₅

 - угол наклона прямой а к горизонтальной пл.пр.

• - угол наклона прямой а к фронтальной пл. пр.

На прямой общего положения а задаем отрезок АВ АВ|  а
1 вариант П2П4П1 П4 || а х14 || а1	2 вариант П1П5П2 П5 || а х25 || а2

Рисунок 4.5

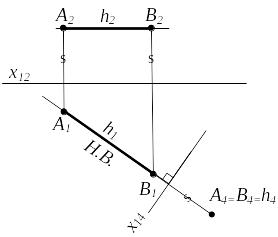
Задача 2. Прямую уровня сделать проецирующей прямой (рис. 4.6 и 4.7) .

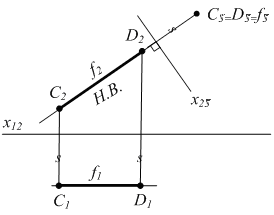
горизонталь h	фронталь f
П2  П4  П1 П4  h x14  h1	П1  П5  П2 П5  f x25  f2
Рисунок 4.6	Рисунок 4.7

Алгоритм преобразования (рис.4.6):

1. П₄h ;

2.  - проецирование ортогональное;

3.  - const .

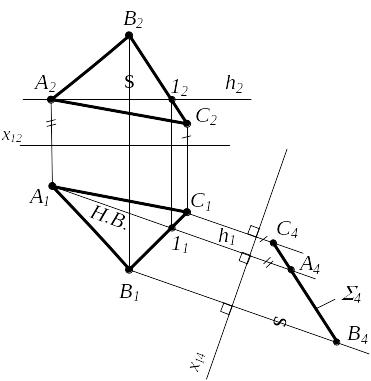
Задача 3. Плоскость общего положения сделать проецирующей плоскостью в новой системе проекций.

Для решения этой задачи новую плоскость проекций нужно расположить перпендикулярно данной плоскости общего положения и перпендикулярно одной из плоскостей проекций. Это возможно, если направление проецирования совпадает с направлением соответствующих линий уровня пл. общего положения. Тогда все линии уровня изобразятся точками на новой плоскости проекций и дадут вырожденную в прямую проекцию плоскости.

(АВС) - общего положения П2  П4  П1 П 4   h   (h  A) П4  h x14  h1

Рисунок 4.8

П₄(h₁)

1) П₂  П₄  

2)  - проецирование ортогональное;

3)  - const .

Если плоскость проходит через перпендикуляр к другой плоскости, то она перпендикулярна ей. Т.е., если x₁₄h₁, то П₄ или плоскость вырождается в прямую ₄ .

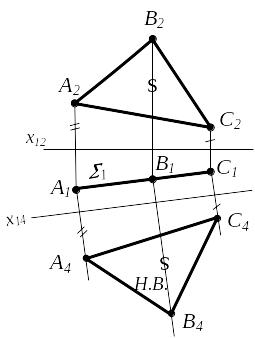
Задача 4. Ввести новую плоскость проекций так, чтобы проецирующая плоскость стала бы плоскостью уровня в новой системе проекций (параллельна новой плоскости проекций).

Решение этой задачи позволяет определить величины плоских фигур.

Новую плоскость проекций нужно расположить параллельно заданной плос­кости.

(АВС)П1 ; П2  П4П1 Т.е. преобразование только такое: П 2  П4 П1 , и одновременно П4    х14  1 Следовательно: АВС  А4В4С4

Рисунок 4.9

Алгоритм преобразования:

1) П₄ ... || 

2)  - проецирование ортогонально новой плоскости;

3)  - const - сохранение расстояний.

Если выполнить 1 и 2 задачи друг за другом на одном чертеже, прямая общего положения может преобразоваться в проецирующую прямую.

Последовательное решение 3 и 4 задач на одном чертеже позволяет плоскость общего положения преобразовать в плоскость уровня.