6.2.3 Расчѐт поперечных рѐбер

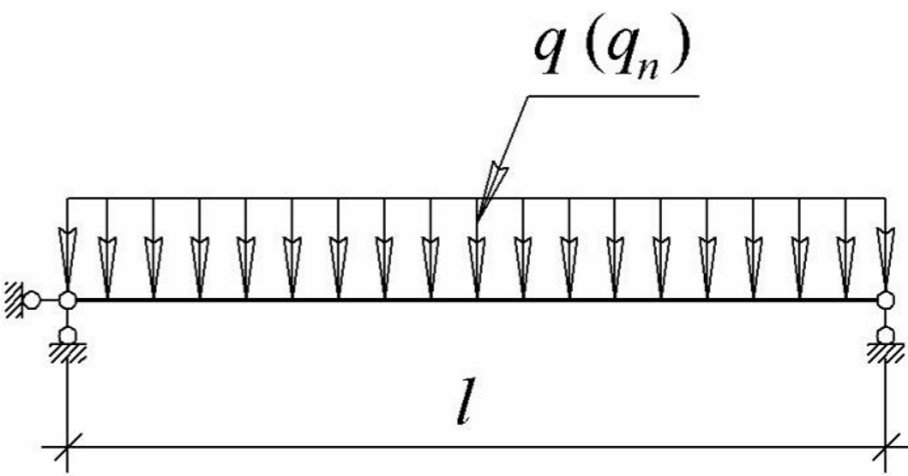
Поперечные рѐбра щитов покрытия рассчитываются по схеме простых двухопорных балок, несущих равномерно распределѐнную нагрузку (комбинация нагрузок, действующих на крышу «сверху вниз»), собираемую с соответствующей грузовой площади (рис. 6.7). Расчѐтная схема поперечных рѐбер показана на рис. 6.8.

Сечение поперечных рѐбер принимается, как правило, из прокатных швеллеров или уголков.

Сечение продольного ребра назначается по требуемому моменту сопротивления:

W_треб . (6.72)

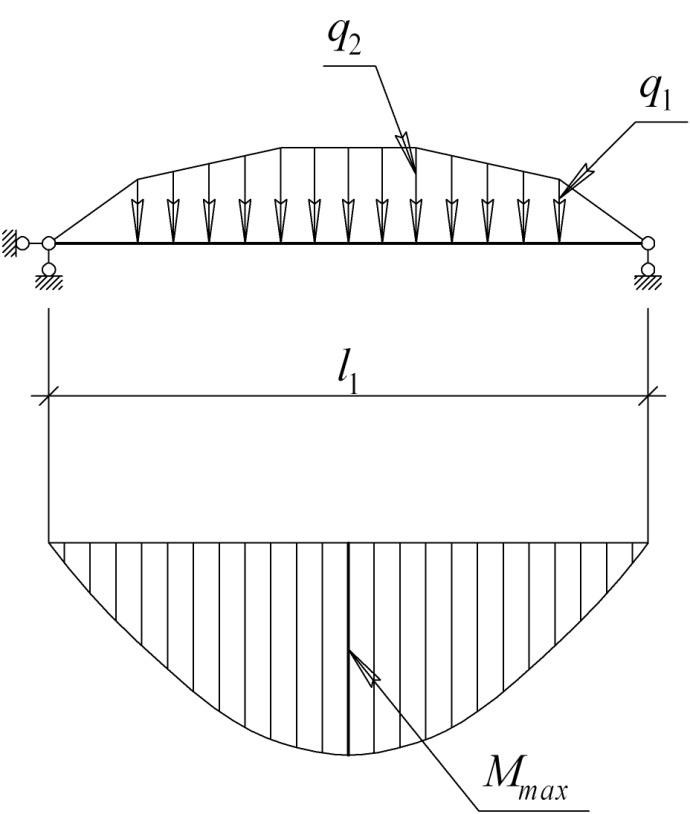
Рис.6.8 – Расчѐтная схема поперечных рѐбер

Поперечное ребро проверяется на прочность по формуле (28) [2]:

. (6.73)

Принятое сечение ребра необходимо проверить по предельному прогибу:

f_max [ f ], (6.74)

где [f] – предельный прогиб по [5].

Усилия и прогибы могут быть получены как численными, так и аналитическими методами (табл. 6.7).

Таблица 6.7 – Максимальные изгибающие моменты и максимальные прогибы в простых балках

Схема нагрузки	Максимальный изгибающий момент	Максимальный прогиб
	2 M max 8	5 qn l4 fmax 3 84 E Ix
	M max 8 6
	2 M max 12	qn l4 fmax 120 E Ix

6.2.4 Расчѐт радиальных рѐбер

В щитовых конических и сферических крышах основными несущими элементами являются радиальные рѐбра, установленные с шагом по окружности корпуса резервуара b, определяемым дорожным габаритом кровельного щита (рис. 6.9).

Рѐбра удобно конструировать из швеллеров, что обусловлено конструкцией щита. В качестве сечения могут быть приняты двутавры.

Расчѐтное значение нагрузки p определяется по формуле:

p q b, (6.75)

где q – расчѐтная равномерно распределѐнная нагрузка по площади; b – ширина грузовой площади.

Для расчѐта принимается комбинация нагрузок с максимальным по модулю значением («сверху вниз» или «снизу вверх»).

6.2.4.1 Расчѐт радиальных рѐбер резервуара с центральной стойкой

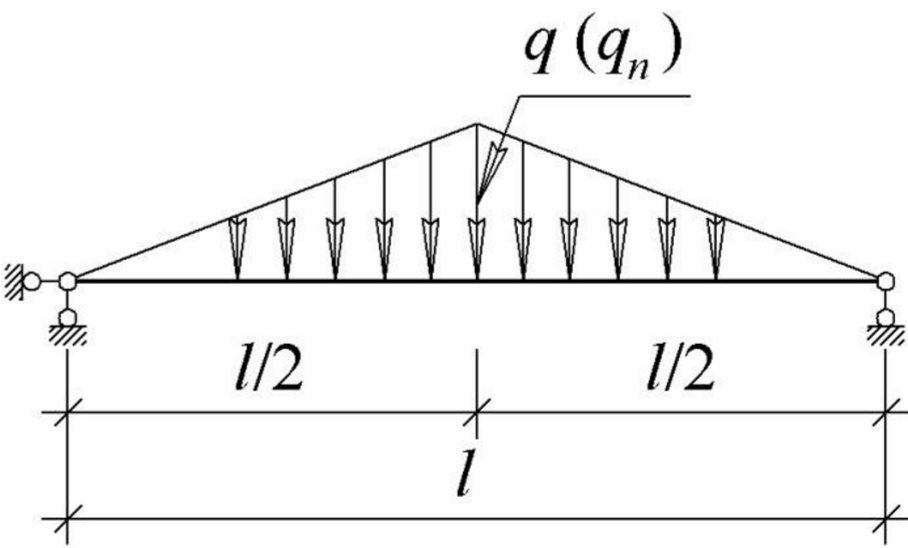
Расчѐт радиальных балок щитов при наличии центральной стойки выполняется по схеме просто балки на двух опорах (стенки и центральной стойки), воспринимающей нагрузки от грузовой площади в виде треугольника

(рис. 6.9).

Расчѐтная схема радиальных рѐбер резервуара с центральной стойкой показана на рис. 6.10.

Максимальный изгибающий момент в шарнирно опѐртой балке, нагруженной сплошной нагрузкой треугольного вида:

M_max , (6.76)

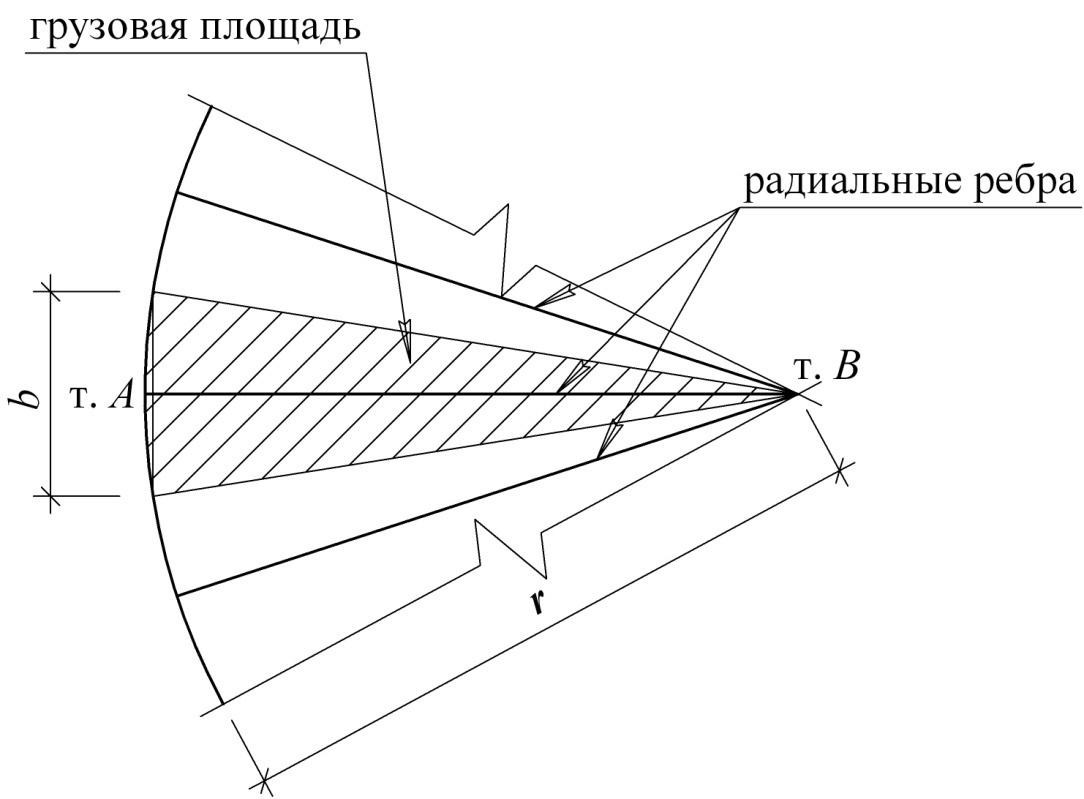
Рис.6.9 – Определение грузовых площадей для радиальных рѐбер

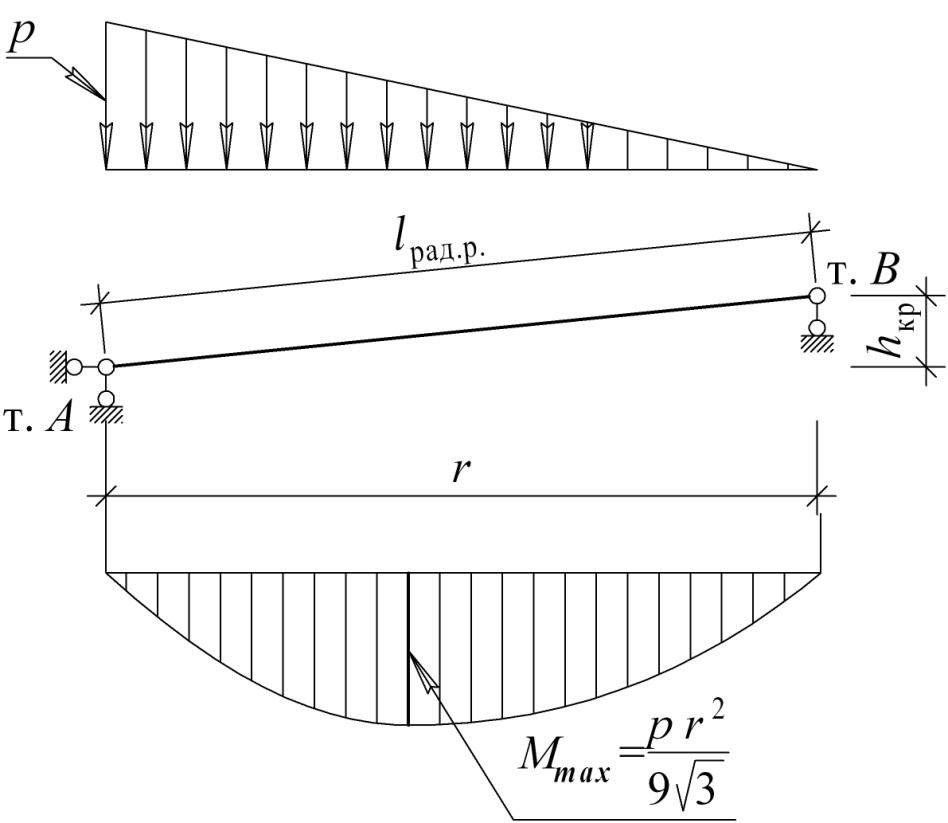
Рис.6.10 – Расчѐтная схема радиальных рѐбер резервуара с центральной стойкой

Максимальный прогиб шарнирно опѐртой балки, нагруженной сплошной нагрузкой треугольного вида:

fmax ^{pn r4} , (6.77)

153 E I_x

где p_n – нормативное значение нагрузки, определяемое по формуле:

p_n q_n b, (6.78)

q_n – нормативная равномерно распределѐнная нагрузка по площади;

Е – модуль упругости прокатной стали и стальных отливок; I_x – момент инерции сечения.

Сечения радиальных рѐбер принимают обычно в виде прокатных двутавров или швеллеров.

Требуемый момент сопротивления сечения из условия обеспечения прочности можно определить по формуле (6.72).

Требуемый момент инерции сечения из условия обеспечения жѐсткости (при предельном прогибе [ f ], табл. 19 [5]):

I_треб ^{pn r4} . (6.79)

153 E [ f ]

Радиальное ребро проверяется на прочность по формуле (6.73), на жѐсткость по формуле (6.74).