Варианты задач для самостоятельного решения
Найти оптимальные решения задач.
Задача 41.
Решить задачу об оптимальном распределении ресурсов в количестве 6 усл.ед. между 3 предприятиями. Эффективность использования средств задана в табл.38.
Таблица 38. Эффективность использования средств
x |
f1(x) |
f2(x) |
f3(x) |
1 |
2 |
3 |
4 |
2 |
6 |
6 |
8 |
3 |
9 |
12 |
10 |
4 |
16 |
16 |
12 |
5 |
20 |
18 |
16 |
6 |
24 |
22 |
20 |
Задача 42.
О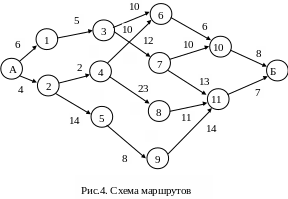
пределить
такой путь из пункта А в пункт Б, общая
стоимость передвижения по которому
будет минимальной.
Заключение
Рассмотренные методы решения могут быть применены для решения большого круга различных по физической и экономической природе задач.
Правильное построение экономико-математической модели задачи, понимание физического и экономического смысла искомых решений является необходимым условием для получения правильного, адекватного решения.
Литература
Исследование операций в экономике: Учеб.пособие для вузов / Н.Ш.Кремер, Б.А.Путко, И.М.Тришин, М.Н.Фридман; Под ред.проф. Н.Ш.Кремера. – М.: ЮНИТИ, 2005.
Экономико-математические методы и модели. Задачник: уч.-метод. пособие / кол.авторов; под ред. С.И.Макарова, С.А.Севастьяновой. – М.: КНОРУС, 2008. – 208 с.
Вентцель, Е.С. Исследование операций. /Е.С.Вентцель. – М.: Сов. радио, 1972.
Просветов, Г.И. Методы оптимизации. Учебно-практическое пособие / Г.И.Просветов. - М.: Изд-во «Альфа-Пресс», 2009. - 168 с.
Лукиных, И.Г. Методы оптимальных решений. Учебное пособие /И.Г.Лукиных. – Киров: ПРИП ФГБОУ ВПО «ВятГУ», 2012. – 63 с.
Содержание
Введение 3
1. Задачи линейного программирования 3
1.1. Решение задачи на максимум линейной функции 4
1.2. Варианты задач для самостоятельного решения 7
1.3. Отыскание минимума линейной функции 9
1.4. Варианты задач для самостоятельного решения 11
1.5. Особые случаи симплексного метода 15
1.6. Варианты задач для самостоятельного решения 19
1.7. Метод искусственного базиса (М-метод) 22
1.8. Варианты задач для самостоятельного решения 24
2. Двойственные задачи 27
2.1. Варианты задач для самостоятельного решения 29
2.2. Экономическая интерпретация двойственной задачи 30
2.3. Решение двойственной задачи и определение интервалов устойчивости двойственных оценок оптимального решения. 32
2.4. Варианты задач для самостоятельного решения 34
2.5. Задачи целочисленного программирования 35
2.6. Варианты задач для самостоятельного решения 38
3. Транспортная задача 40
3.1. Постановка и решение транспортной задачи 40
3.2. Проверка плана на оптимальность. Метод потенциалов 44
3.3. Варианты задач для самостоятельного решения 49
4. Задачи динамического программирования 51
4.1. Задача о распределении средств между предприятиями 51
4.2. Варианты задач для самостоятельного решения 55
Заключение 56
Литература 56
Содержание 58
Учебное издание
Лукиных Ирина Григорьевна
МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ
Учебно-методическое пособие
Подписано в печать . Печать цифровая. Бумага для офисной техники.
Усл. печ. л. . Тираж 50 экз. Заказ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Вятский государственный университет»
610000, Киров, ул. Московская, 36, тел.: (8332) 64-23-56, http://vyatsu.ru