1. Задача о распределении средств между предприятиями

Рассмотрим схему решения задач динамического программирования с использованием уравнений Беллмана на примере задачи о распределении средств.

Пример 15. Планируется деятельность трех предприятий на очередной год. Начальные средства, которые следует распределить, s₀=5 усл.ед. Размеры вложения в каждое предприятие кратны 1 усл.ед. Средства x, выделенные предприятию k, приносят в конце года прибыль f_k(x), k=1,2,3. Функции f_k(x) заданы таблично (табл. 36). Принято считать, что:

- прибыль f_k(x) не зависит от вложения средств в другие предприятия;

- прибыль выражается в одних условных единицах;

- общая прибыль равна сумме прибылей, полученных от каждого предприятия.

Определить, какое количество средств нужно выделить каждому предприятию, чтобы общая прибыль была наибольшей.

Таблица 36. Эффективность использования средств

x	f1(x)	f2(x)	f3(x)
1	8	6	4
2	10	9	8
3	12	12	12
4	14	15	16
5	16	18	20

Решение. Построим математическую модель задачи. Обозначим через x_k количество средств, выделенных предприятию k. Общая прибыль равна

(4.1)

Переменные x_k удовлетворяют ограничениям:

(4.2)

Требуется найти переменные x₁, x₂, x₃, удовлетворяющие системе ограничений (4.2), при которых функция (4.1) достигает максимума.

Особенность модели состоит в том, что хотя ограничения линейные и переменные целочисленные, методы целочисленного линейного программирования применять нельзя, так как функции f_k(x) заданы таблично.

Схема решения задачи методом динамического программирования имеет следующий вид:

- процесс распределения средств s₀=5 можно рассматривать как трехшаговый, номер шага совпадает с номером предприятия;

- выбор переменных x₁, x₂, x₃ – управление соответственно на I, II и III шаге;

- – конечное состояние процесса распределения, все средства вложены в производство.

Графически схема распределения показана на рис.1.

У равнения состояний имеют вид:

(4.3)

где s_k – параметр состояния, количество средств, оставшихся после k-го шага, т.е. эти средства остается распределить между (3 – k) оставшимися предприятиями.

Рассмотрим функцию – условную оптимальную прибыль, полученную от предприятий k, (k+1),…,3, если между ними оптимальным образом распределялись средства . Допустимые управления на шаге k удовлетворяют условию: .

Уравнения, связывающие оптимальную прибыль на каждом шаге, имеют вид:

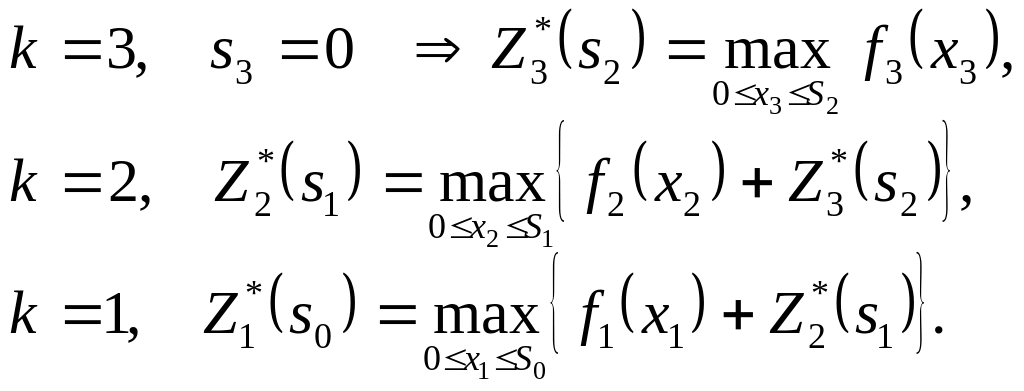(4.4)

Последовательно решает уравнения, проводя условную оптимизацию каждого шага (см. рис.1).

III шаг. В табл. 36 прибыль f₃(x) монотонно возрастает, поэтому все средства, оставшиеся к III шагу, следует вложить в предприятие 3. При этом для возможных значений s₂=0,1,…5 получим:

(4.5)

II шаг. Делаем все предположения относительно остатка средств s₁ ко II шагу, т.е. после выбора x₁. s₁ может принимать значения 0, 1, 2, 3, 4, 5. В зависимости от этого выбираем , находим и сравниваем для разных при фиксированном значения суммы . Для каждого наибольшее из этих значений - условная оптимальная прибыль, получаемая при оптимальном распределении средств между 2-м и 3-м предприятиями. Оптимизация записана в табл.37 при k=2. Для каждого значения оптимальные значения и записаны в графах 5 и 6.

I шаг. Условная оптимизация проведена в табл.37 при k=1 для значения s₀=5. Например, если x₁=0, то s₁=5, прибыль, полученная от трех предприятий при условии, что s₁=5 ед. средств между оставшимися двумя предприятиями будут распределены оптимально, равна . Значение взято из столбца 6 табл.37 при s₁=5. Если x₁=1, то s₁=4, суммарная прибыль при условии оптимального распределения ресурсов равна . Значение взято из табл.36, - из столбца 6 табл.37 при s₁=4. Аналогично вычислены остальные значения столбца 8 табл.37.

Оптимальное решение выделено в табл.37 жирным курсивом: максимум суммарной прибыли при условии, что предприятию 1 выделена 1 усл.ед., предприятию 2 – 1 усл.ед., предприятию 3 – 3 усл.ед.

Достоинством метода является возможность анализа решения на чувствительность к изменению s₀ и числа шагов (предприятий), а также безразличие метода к способу задания функций .

Таблица 37. Оптимизация распределения ресурсов

sk-1	xk	sk	k=2			k=1
1	2	3	4	5	6	7	8	9
0	0	0	0	0	0	0	0	0
1	0	1	0+4=4			0+6=6
	1	0	6+0=6	6	1	8+0=8	8	1
2	0	2	0+8=8			0+10=10
	1	1	6+4=10	10	1	8+6=14	14	1
	2	0	9+0=9			10+0=10
3	0	3	0+12=12			0+14=14
	1	2	6+8=14	14	1	8+10=18	18	1
	2	1	9+4=13			10+6=16
	3	0	12+0=12			12+0=12
4	0	4	0+16=16			0+18=18
	1	3	6+12=18	18	1	8+14=22	22	1
	2	2	9+8=17			10+10=20
	3	1	12+4=16			12+6=18
	4	0	15+0=15			14+0=14
5	0	5	0+20=20			0+22=22
	1	4	6+16=22	22	1	8+18=26	26	1
	2	3	9+12=21			10+14=24
	3	2	12+8=20			12+10=22
	4	1	15+4=19			14+6=20
	5	0	18+0=18			16+0=16