Задачи целочисленного программирования
Во многих практических задачах линейного программирования переменные по своему смыслу должны принимать только целочисленные значения. Такие задачи называют задачами целочисленного программирования. Из методов целочисленной оптимизации наиболее часто используется метод отсечения Гомори. Рассмотрим алгоритм и пример решения задачи с применением этого метода.
Задача линейного программирования решается симплексным методом без учета условия целочисленности.
Если все компоненты оптимального решения целые, то решение является оптимальным и для задачи целочисленного программирования.
Если среди компонент оптимального решения есть нецелые, то к ограничениям задачи добавляют новое ограничение, называемое правильным отсечением, и удовлетворяющее следующим условиям: оно должно быть линейным, должно отсекать найденный оптимальный нецелочисленный план, не должно отсекать ни одного целочисленного решения.
Пусть задача линейного программирования имеет конечный оптимум и на последнем шаге ее решения симплексным методом получены уравнения, выражающие основные переменные x1, x2,…xm через неосновные xm+1, xm+2,…xn оптимального решения:
(2.20)
Пусть в оптимальном
решении
– нецелая компонента. Тогда неравенство
(2.21)
где {} – дробная часть числа, обладает свойствами правильного отсечения.
Если в оптимальном решении несколько нецелых компонент, то среди них выбирают компоненту с наибольшей целой частью и по соответствующему уравнению строят правильное отсечение.
Введением дополнительной неотрицательной переменной неравенство (2.21) преобразуется в уравнение
(2.22)
и включается в систему ограничений (2.20).
Полученная расширенная задача решается симплексным методом. Если её оптимальное решение будет целочисленным, исходная задача решена. В противном случае алгоритм повторяется с п.3.
Если задача разрешима в целых числах, то оптимальный целочисленный план будет найден за конечное число шагов.
Если в процессе решения появится уравнение, выражающее основную переменную через неосновные, с нецелым свободным членом и целыми остальными коэффициентами, то соответствующее уравнение и, следовательно, вся задача, не имеют решения в целых числах.
Пример 12. На трикотажной фабрике планируется выпуск двух видов детских платьев: «Ажурное» и «Нарядное». На 1 платье «Ажурное» требуется 100 г шерстяной пряжи, 200 г акриловой пряжи и 1 единица рабочего времени; на 1 платье «Нарядное» – 350 г шерстяной пряжи, 50 г акриловой пряжи и 1 единица рабочего времени. Всего имеется 30 кг шерстяной пряжи, 13 кг акриловой пряжи и 120 единиц рабочего времени. По плану предусматривается выпуск не менее 110 платьев. Требуется определить оптимальное число платьев каждого вида для получения максимальной прибыли, если прибыль от реализации платья «Ажурное» составляет 100 рублей, а от реализации платья «Нарядное» – 200 рублей.
Решение. Составим математическую модель задачи.
Пусть x1
– количество платьев «Ажурное», x2
– количество платьев «Нарядное». Целевая
функция:
.
Запишем ограничения:
(2.23)
Используя симплексный метод без учета целочисленности переменных x1 и x2, получаем следующее оптимальное решение:
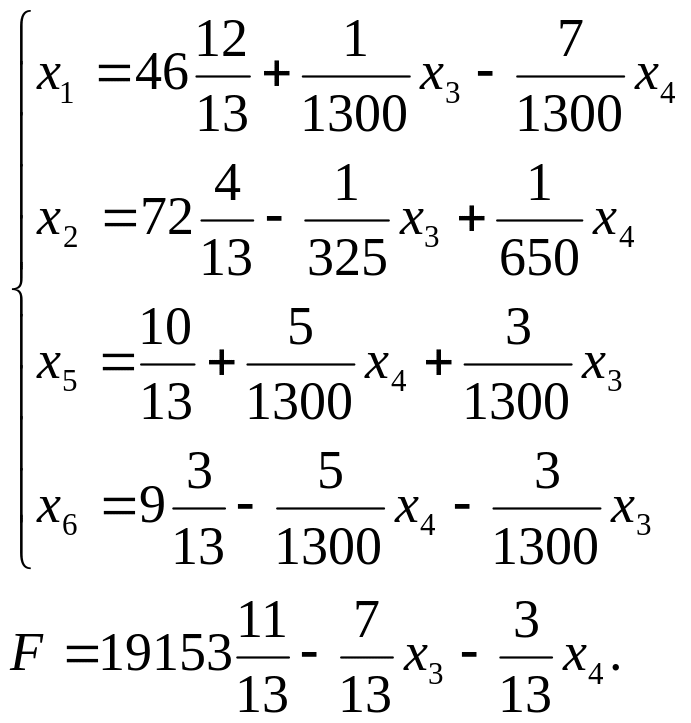(2.24)
Решение является нецелочисленным. Переменная x2 имеет наибольшую целую часть, по уравнению, соответствующему этой переменной строим правильное отсечение:
. (2.25)
Далее следует добавить неравенство (2.25) к решению (2.24), ввести дополнительную переменную x7, и продолжить решение симплексным методом. Выполните эти шаги самостоятельно. В результате получим:
(2.26)
Решение является
оптимальным и целочисленным:
.
Максимальное значение целевой функции
Fmax=19100.
Ответ: максимальная прибыль 19100 руб., 47 платьев вида «Ажурное», 72 платья вида «Нарядное». Останется 100 г шерстяной пряжи и 1 единица рабочего времени. Неосновная переменная x4 не входит в выражение целевой функции на оптимальном решении, следовательно, ее изменение не изменяет значения Fmax. Но для того, чтобы решение оставалось допустимым, переменная x4 может принимать значения от 0 до ½. Только при x4=0 решение задачи является целочисленным.