3. Решение двойственной задачи и определение интервалов устойчивости двойственных оценок оптимального решения.

На основании полученного оптимального решения двойственной задачи можно провести анализ устойчивости решения относительно изменения запасов ресурсов. Т.е. можно определить, в каких интервалах допустимо изменять значения запасов ресурсов, чтобы двойственные оценки оставались неизменными.

Пример 11. При решении двойственной задачи, составленной в примере 9, симплексным методом, получаются следующие результаты.

Базисные переменные: y₁, y₂, неосновные переменные: y_3, y₄, y₅.

(2.8)

Выражение целевой функции на оптимальном решении:

(2.9)

Предположим, что запасы b_i ресурсов каждого вида изменились на ∆b_i единиц (i=1, 2, 3). Запишем исходное выражение целевой функции (1.42) с новыми коэффициентами:

(2.10)

Подставим в это выражение полученные выражения для оптимальных решений у₁ и у₂ из системы (1.42), и после преобразований получим:

(2.11)

Для того чтобы полученное решение двойственной задачи оставалось оптимальным, коэффициенты при неосновных переменных в целевой функции должны остаться неотрицательными:

(2.12)

В том случае, когда запасы изменяются одновременно по нескольким видам ресурсов, найти интервалы устойчивости как решение системы неравенств (2.12) в общем случае затруднительно. Однако можно проверить, удовлетворяют ли конкретные изменения запасов ресурсов системе (2.12).

Например, если , то решение останется оптимальным, т.к. все неравенства удовлетворены. При этом . Решение исходной задачи следует из соответствия решений взаимно-двойственных задач (см. таблицу 21): оптимальное значение x₁ равно коэффициенту при переменной y₄, значение x₂ равно коэффициенту при переменной y₅, значение x₅ равно коэффициенту при переменной y₃ в выражении целевой функции (1.46):

. (2.13)

Если , то первое неравенство не выполнено. Переменная у₃ должна быть переведена в базисные переменные, и оптимальные значения двойственных оценок изменятся.

Определим интервалы устойчивости оптимального решения двойственной задачи по каждому ресурсу в отдельности.

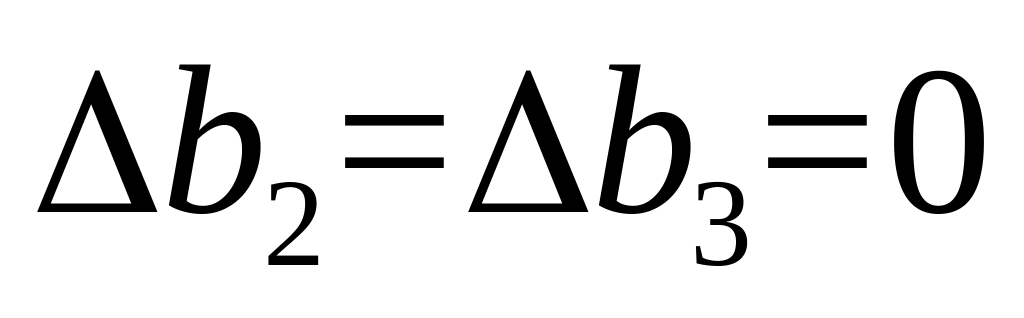1. Полагая , получаем систему неравенств

(2.14)

Следовательно, решение останется оптимальным, если

. (2.15)

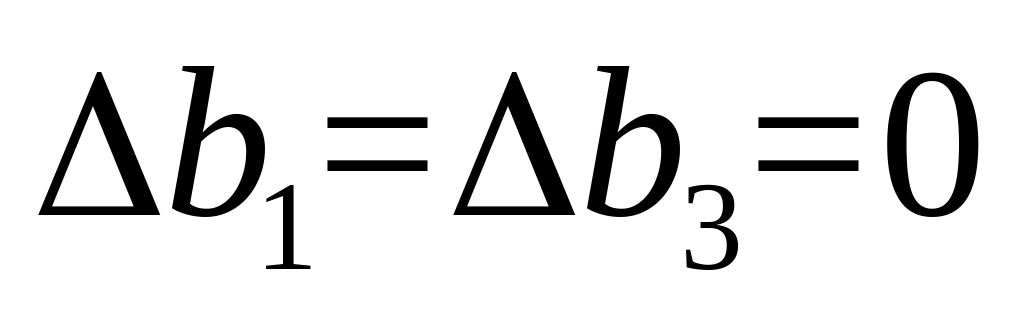2. Полагая , получаем систему неравенств

(2.16)

Следовательно, решение останется оптимальным, если

. (2.17)

3. Полагая , получаем неравенство

. (2.18)

Следовательно, решение останется оптимальным, если

. (2.19)

Итак, формулы (2.15), (2.17) и (2.19) определяют интервалы устойчивости двойственных оценок по каждому ресурсу при условии, что остальные ресурсы остаются в неизменном количестве.

4. Варианты задач для самостоятельного решения

Задача 26.

Составить и решить задачу, двойственную к задаче 1. Найти интервалы устойчивости двойственных оценок. Проанализировать и оценить целесообразность включения в план производства третьего вида корма, если в 1 набор входит 10 г фруктов, 60 г злаков, 30 г орехов, а прибыль от реализации 1 набора этого корма составляет 3,5 денежных единицы.

Задача 27.

Составить и решить задачу, двойственную к задаче 2. Найти интервалы устойчивости двойственных оценок. Проанализировать и оценить целесообразность включения в план производства третьего вида костюмов, если на 1 костюм необходимо 2 м шерсти, 1,5 м лавсана и 0,8 человеко-дней трудозатрат, а прибыль от реализации 1 костюма составляет 150 денежных единиц.

Задача 28.

Составить и решить задачу, двойственную к задаче 3. Найти интервалы устойчивости двойственных оценок. Проанализировать и оценить целесообразность включения в план производства третьего вида продукции (календарей), если на 1 календарь необходимо 1 условный лист бумаги, и 1 час рабочего времени, а прибыль от реализации 1 календаря составляет 0,5 доллара.

Задача 29.

Составить и решить задачу, двойственную к задаче 4. Найти интервалы устойчивости двойственных оценок. Проанализировать и оценить целесообразность включения в план производства продукции П4, если на 1 единицу продукции необходимо 6 единиц ресурса Р1, 4 единицы ресурса Р2, 2 единицы ресурса Р3, 1,5 м лавсана и 0,8 человеко-дней трудозатрат, а прибыль от реализации 1 костюма составляет 150 денежных единиц.

Задача 30.

Составить и решить задачу, двойственную к задаче 5. Найти интервалы устойчивости двойственных оценок. Проанализировать и оценить целесообразность включения в план производства 5-го вида ткани (смесовая), если на выпуск 1 партии ткани необходимо 40 мин. рабочего времени, 180 единиц денежных ресурсов, а величина партии составляет 100 м.