Лабораторная работа 4
Исследование нестационарных процессов течения жидкости через гидродроссель
4.1 Цель работы и содержание работы
Исследовать режимы течения жидкости через гидродроссель, определение характеристик гидроаккумулятора.
4.2 Краткие теоретические сведения Истечение жидкости из отверстия в тонкой стенке
Истечением называется частный случай течения жидкости, при котором потенциальная энергия жидкости, находящейся в резервуаре, превращается с большими или маленькими потерями в кинетическую энергию струи или капель.
Законы истечения жидкости имеют большое практическое значение, поскольку они применяются при решении многих технических задач, в том числе и в авиационной технике (подача топлива в камеры сгорания авиационных двигателей, течение через жиклеры в элементах автоматики жидкостно-газовых систем, в амортизационных стойках шасси и др.).
Задача об истечении обычно сводится к определению скорости истечения и расхода жидкости. Наиболее просто и точно она решается в случае, когда напор одинаков по всему поперечному сечению отверстия. Этому требованию удовлетворяет случай истечения из горизонтального отверстия в дне сосуда (рис.4.1).
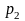
Рис. 4.1. Истечение из донного отверстия
Рассмотрим
течение жидкости, находящейся под
давлением
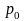из резервуара через относительно
небольшое круглое отверстие с диаметром
в тонкой стенке дна, расположенное на
глубине
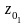в воздушное пространство с давлением
.
Будем
полагать, что свободная поверхность и
боковые стенки резервуара находятся
далеко от отверстия и не влияют на приток
жидкости к отверстию, поэтому частицы
жидкости приближаются к нему из всего
объема. Кроме того, примем, что уровень
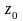поддерживается постоянным.
Как
показывает опыт, струя жидкости отрывается
от стенки у кромки отверстия и несколько
сжимается. Сжатие струи обусловлено
необходимостью плавного перехода от
различных направлений движения частиц
жидкости в резервуаре к осевому
направлению их движения в струе. На
расстоянии, равном примерно диаметру
отверстия, струя принимает цилиндрическую
форму с диаметром
.
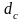Степень сжатия струи оценивается
коэффициентом сжатия
,
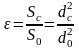(4.1)
где
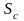и
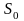– площади поперечных сечений струи и
отверстия соответственно.
Запишем
уравнение Бернулли для сечений 0 – 0
(свободная поверхность) и 2 – 2, где струя
уже приняла цилиндрическую форму, и
давление в ней стало равным
.
Будем считать, что распределение
скоростей по сечению струи равномерное,
т.е.
,
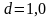
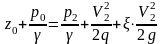(4.2)
где
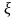– коэффициент сопротивления отверстия.
Введя расчетный напор
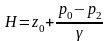
получим выражение для скорости истечения
,
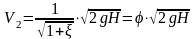(4.3)
здесь
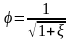– коэффициент скорости.
В
случае идеальной жидкости коэффициент
сопротивления отверстия
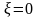и скорость истечения равна теоретической
.
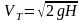(4.4)
Таким образом, физический смысл коэффициента скорости в том, что он показывает отношение действительной скорости истечения к теоретической.
Расход жидкости при истечении
.
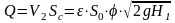(4.5)
Вводится
коэффициент расхода
.
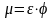Тогда
.
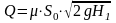(4.5)
Безразмерные коэффициенты , , , зависят от формы отверстия и числа Re, подсчитанного по теоретической скорости (5.4), т.е.
.
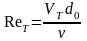На
рис.4.2 приведены зависимости указанных
коэффициентов от
для круглого отверстия.
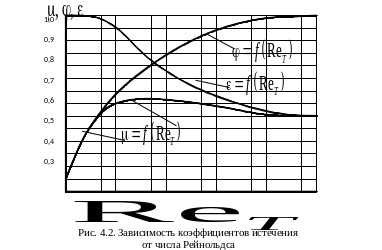
Из
приведенных графиков видно, что с
увеличением чисел
коэффициент скорости
возрастает. Это происходит потому, что
из-за уменьшения роли сил вязкости
уменьшается коэффициент сопротивления
.
При
коэффициент
,
а
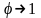(случай идеальной жидкости). Коэффициент
сжатия струи
при увеличении
изменяется от 1,0
до 0,61.Изменение
коэффициента расхода
является следствием изменения
коэффициентов
и .
Наибольшее значение
достигается при
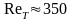и равно
.
Следует
отметить, что при больших числах
(маловязкие жидкости) коэффициенты ,
и
изменяются слабо, поэтому в расчетах
обычно принимают следующие их значения:
,
,
.
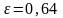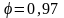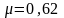Если отверстие сделано не в дне, а в боковой стенке резервуара (вертикальной или наклонной), то приведенные формулы для скорости истечения и расхода, строго говоря, неприменимы. В этом случае напор не будет одинаковым во всем сечении отверстия и параметры истечения необходимо определять интегрированием по площади сечения параметров элементарных площадок отверстия. Однако можно показать, что если размеры отверстия малы по сравнению с размерами резервуара, то погрешности оказываются незначительными и для расчетов можно использовать формулы (4.1,…,4.6).
Истечение из отверстия при несовершенном сжатии струи
При рассмотренном истечении струя претерпевает наибольшее сжатие или, как принято называть, имеет место совершенное сжатие струи.
Если же боковые стенки резервуара расположены достаточно близко от отверстия, то они оказывают влияние на приток жидкости к отверстию и этот случай называется несовершенным сжатием струи.
В авиационных гидросистемах чаще всего используются цилиндрические резервуары, диаметры которых соизмеримы с диаметрами отверстий для истечения. При истечении из таких резервуаров через круглое отверстие, расположенное по оси резервуара (рис.4.3), существует эмпирическая зависимость для коэффициента сжатия
,
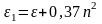(4.7)
г
де
,
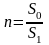а
определяется, как рассмотрено выше. При
этом принимается
,
а
.
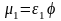