Лабораторная работа 3

Определение коэффициентов местных гидравлических соединений

3.1 Цель работы и содержание работы

Исследовать течение жидкости в трубопроводах через местные гидравлические сопротивления, определить потери напора на этих участках.

3.2 Краткие теоретические сведения

Местные гидравлические сопротивления

Для осуществления расчета гидравлических систем необходимо изучить природу и методику расчета местных гидравлических сопротивлений, то есть таких элементов гидросистемы, в которых вследствие изменений размеров и конфигураций русла происходит изменение скорости потока и потери энергии потока.

Физическая природа местных гидравлических сопротивлений в основном одна: энергия потока расходуется на вихреобразования, связанные с отрывом потока от стенок, вихреобразование в потоке и т.д.

Вначале рассмотрим простейшие местные гидравлические сопротивления, связанные с расширением русла, сужением русла и с поворотом русла.

Внезапное расширение русла

При протекании в зоне расширения жидкость (рисунок 3.1) встречает резкое повышение давления, которое преодолевается за счет скоростного напора. На периферии скорость потока стремится к нулю и создается зона обратного движения жидкости. Запишем уравнение Бернулли для этого случая:

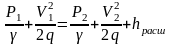, (3.1)

где h расширения – потери напора, связанные с внезапным расширением русла.

Для определения и расширения запишем уравнение изменения количества движения для объема 1-2.

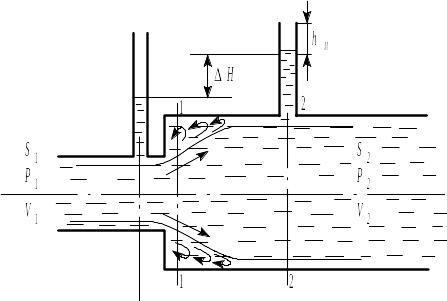
Рисунок 3.1

Импульс сил – 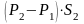, а секундное изменение количества движения ,

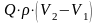тогда

,

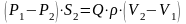учитывая, что 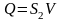, и разделив на 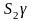, получим

,

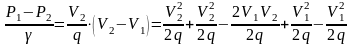то есть

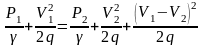. (3.2)

Сравнивая (3.1) и (3.2), получаем:

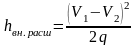. (3.3)

Таким образом, при внезапном расширении потока потеря напора равна напору потерянной скорости и не зависит ни от рода жидкости, ни от исходного давления, ни от наклона трубы.

Используя уравнение расхода

,

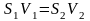получим

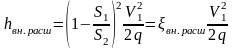, (3.4)

где коэффициент сопротивления

.

При подводе жидкости в резервуар больших размеров, можно считать, что 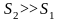, тогда

, а .

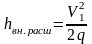То есть вся кинетическая энергия подводимого потока уходит на преодоление сопротивления неподвижной жидкости в резервуаре.

Течение в диффузоре

Анализ рисунка 3.1 показывает, что соответствующим выбором профилирования места расширения русла можно уменьшить потери на вихреобразования. Таким простейшим профилем является коническая расширяющаяся труба – диффузор (рисунок 3.2).

Рисунок 3.2

Течение жидкости в диффузоре сопровождается плавным уменьшением скорости и увеличением давления. Частицы жидкости при течении вдоль диффузора преодолевают повышающееся давление за счет своей кинетической энергии. У стенок (за счет трения в пограничном слое) скорость и кинетическая энергия уменьшаются более значительно, Здесь возникает обратное течение – срыв потока (вихреобразование). Таким образом, в диффузоре существует потери на трение о стенки и потери на вихреобразование при расширении

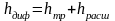. (3.5)

Здесь потери на трение

.

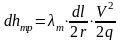Но

, ,

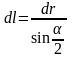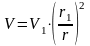тогда

.

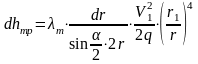Интегрируя от 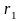до 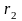, получаем:

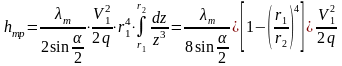. (3.6)

Отношение 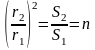называется степенью расширения диффузора.

С учетом этого выражение (3.6) принимает вид:

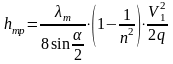. (3.7)

Второе слагаемое в (3.5) – потери напора на расширение – аналогично, по своей природе, внезапному расширению и только меньше последнего по величине.

Поэтому

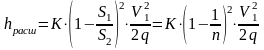, (3.8)

где K – коэффициент смягчения.

Для  = 520 K  sin..

Подставим (3.7) и (3.8) в (3.5). Окончательно получаем

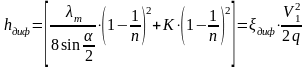. (3.9)

Таким образом, потери в диффузоре зависят как от коэффициента трения, так и от угла раствора диффузора и степени его расширения.

Анализ опытных данных показывает, что для конических диф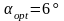фузоров , для плоских диффузоров 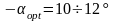. На рисунке 3.3 показана зависимость коэффициента сопротивления конического диффузора от угла его раствора.

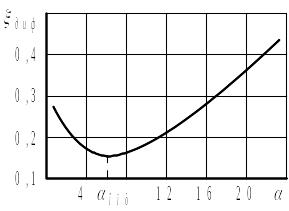
Рисунок 3.3

Если по условиям габаритов невозможно применить 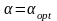, то  увеличивают, но при  > 15  25 целесообразно применить специальные диффузоры с

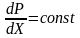
или ступенчатый (рисунок 4.4).

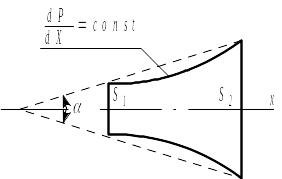
Рисунок 3.4