Заключение

В ходе проектирования были решены задачи нахождения ранних сроков окончания выполнения операторов; построения нитей решения задачи в соответствии с заданной граф-схемой; распределения нитей по ВС, с учетом времени передачи между операторами и между процессорами.

В результате проделанной работы можно сделать вывод, что «Алгоритм распределения программных модулей по узлам ВС» работает верно и позволяет оптимизировать время и число необходимых процессоров для решения поставленной задачи. Данный алгоритм применим для различных топологий ВС, для неограниченного количества операторов. Таким образом, «Алгоритм распределения программных модулей по узлам ВС» является универсальным.

Список используемой литературы

1. Руденко Ю.М., Волкова Е.А. Вычислительные системы. Москва, НИИ РЛ МГТУ им. Н.Э.Баумана, 2010.

2. Корнеев В.В. Параллельные вычислительные системы, Издательство НГТУ, 1999.

3. Хорошевский В.Г. Архитектура вычислительных систем, МГТУ им. Н.Э. Баумана, 2008.

4. Руденко Ю.М. Новый подход к изображению схем алгоритмов для вычислительных систем. Информатика и системы управления в ХХ1 веке. Сборник трудов №7 молодых учёных, аспирантов, и студентов – М,: МГТУ им. Н.Э. Баумана, 2009. 167–181 с.

5. Руденко Ю.М. Построение плана выполнения параллельных алгоритмов на базе граф-схем. Аэрокосмические технологии. Научные материалы МНТК – 2009. Реутов – Москва 2009. 179=181с.

6. Руденко Ю.М. Учёт зависимостей программных модулей по данным и последовательностям их выполнения при параллельных вычислениях. Известия высших учебных заведений. Поволжский регион. Технические науки. № 3 (11), 2009. 67–75 с. 

ПРИЛОЖЕНИЕ 1

Алгоритм построения нитей

1. Просматриваем матрицу SDR по строкам сверху вниз. Если просмотрены все строки, то – конец алгоритма.

2. Если в i-й строке найдено одно число, то вес i-й вершины модифицируется к виду: р_i:=p_i+q_j,i . Если в i-й строке найдено несколько чисел, то веса вершин модифицируются следующим образом: р_j:=p_j+q_i,j ,j={ }, где ,j – множество столбцов, в которых найдены числа, q_i,j – множество весов дуг, принадлежащих i-й строке .

3. Используя модифицированные веса, с помощью алгоритма 6.1.1 вычисляем ранние сроки окончания выполнения операторов.

4. Вычисленные ранние сроки окончания выполнения операторов служат основой для построения диаграммы загрузки ВМ. Каждая строка диаграммы может служить нитью для загрузки в процессор.

ПРИЛОЖЕНИЕ 2.

Алгоритм вычисления ранних сроков окончания выполнения операторов

1. Вычислим t_1,j: =0, где j :=1,…,RS. RS – размер матрицы следования

2. Просматриваются строки матрицы S сверху вниз, выбирается первая необработанная строка матрицы, и осуществляется переход к следующему шагу, если обработаны все строки, то - конец алгоритма.

3. Если выбрана j-я строка, не содержащая единичных элементов, то вычисляем t_1,j: = p_j , где p_j – вес j-го оператора и переходим на шаг 5.

4. Если j-я строка содержит единичные элементы, то вычисляется

t_1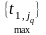,j: = + p_j,

где max , берётся по множеству времён t_1,j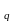 , где j_q – номера элементов j-й строки, равных единице. Если в множестве 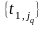есть нулевые элементы, то выполняется шаг 6, иначе выполняется шаг 5.

5. Обработанная j-я строка исключается из рассмотрения. Осуществляется переход на шаг 3.

6. Выбираем столбец j:=j_q и переходим на шаг 3.

Примечание: пункт 6 алгоритма 6.1.1 используется для нетреугольной матрицы S

ПРИЛОЖЕНИЕ 3

Алгоритм распределения программных модулей по узлам Вычислительной сети.

1. Задана ВС с N вычислительных модулей, нумеруемых как {0,1,…,N-1}. Предполагается, что мощность множества удовлетворяет потребность в количестве ВМ для решения поставленной задачи предполагаемым методом.

2. Количество нитей W. Множество нитей Т.

3. Вычислим матрицу расстояний между вычислительными модулями.

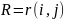
Минимальное расстояние между двумя ВМ равно 1, максимальное – N-2.

4. Для определения показателя близости ВМ определим сумму столбцов матрицы R. 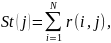j=1,2,…,N. При j=1 показатель близости наилучший.

5. Упорядочим St(j) в порядке возрастания

6. Построим диаграмму ранних сроков окончания выполнения операторов с указанием связей между операторами, с учетов времени передачи между операторами. Образуем множества несвязных между собой пучков нитей { 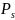}; S={0,1,…,q}.

7. Среди множеств { } найдем множество { 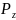}, имеющее нить 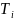с максимальным количеством элементов в множестве 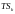(таблице связей к-й нити). Предположим таблица связей имеет 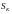элементов.

Примечание: таких множеств нитей может быть несколько, и тогда выбирается любое из них.

8. Составим из связей между нитями множества { } массив MS и обнулим все его элементы.

9. Если степень i-й вершины вычислительной сети есть 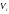, то сравниваем и .

10. Если 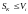, то нить размещается в узле i, и переходим к шагу 12, иначе следующий шаг.

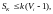11. Если то образуется комплексный узел, в котором один вычислитель основной, остальные являются передающими звеньями.

12. Определим с какой нитью из множества {Pz} связана нить 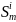. Пусть это будет нить 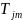=(max ∩Tj), TjϵT.

13. Нить занимает узел j_m вычислительной сети на минимально возможном расстоянии от узла i.

14. Образуем последовательность входящих и исходящих связей i-ой нити с , S₁,S₂,…,S_d (1) из множества MS.

15. Пусть связь S_m ,где mϵ{1,2,..d}, в нити связывает оператор 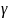с оператором 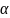нити .Тогда, если связь входящая, то если sT(γ) ≥ fT(α) + r(i,j_m)*ρA,

то переходим на шаг 17,

иначе Pγ=Pγ+ r(i,j_m)*ρA.

Если связь исходящая, то если S_m =0, то

Pα=Pα+ r(i,j_m)*ρA,

иначе если sT(γ) < fT(α), то

sT(γ) = fT(α).

16. Если S_m - входящая связь, то все операторы в нити , начиная с оператора 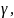сдвинуты по оси времени вправо на величину r(i,j)* ρA. Иначе, аналогично в нити сдвинуты все операторы, начиная с .

17. Связь S_m=1 в массиве связей всех нитей MS.

18. Из последовательности (1) берем следующую связь для рассмотрения, пусть m=m+1 и обозначим эту связь S_m. Если m≤d, то перейти к шагу 15, иначе шаг 19.

19. TS_k= TS_k|T_jm, если TS_k≠0, то переходим к шагу 12, иначе шаг 20.

20. Уменьшим количество нерассмотренных нитей на 1, то есть W=W-1.

Если W=0, то переходим к п.17, иначе выбираем из оставшихся нитей множества {P_z} нить с максимальным числом связей. Пусть эта нить и переходим к шагу 12.

21. Исключить из рассмотрения множества { } и переномеровать множество { }; S={0,1,…,q-1}. Если { } 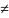0, то перейти к шагу 7, иначе шаг 22.

22. Конец алгоритма.

ПРИЛОЖЕНИЕ 4.1

Матрица следования

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44	Р
1																																													3
2																																													1
3																																													4
4	1	1	1																																										2
5				4.1																																									4
6				4.2																																									5
7				4.3																																									5
8				4.4																																									3
9				4.5																																									7
10				4.6																																									7
11				4.7																																									7
12					1																																								1
13							1																																						7
14								1																																					2
15										1																																			2
16										1																																			1
17										1																																			3
18											1																																		8
19						1						1																																	3
20													1																																3
21									1					1																															3
22																		1																											8
23																			18.1																										2
24																			18.2																										4
25																			18.3																										4
26																				1																									2
27																				1																									2
28																				1																									2
29																				1																									2
30																				1																									2
31																				1																									2
32																				1																									2
33																				1																									2
34																					21.1																								4
35																					21.2																								3
36																						1																							5
37																						1																							7
38																							1																						4
39																																		1											5
40																																				1	1								1
41																																													5
42																																								40.1					2
43																																								40.1					5
44																																								40.2					7

Таблица 1 - Расширенная матрица следования.

ПРИЛОЖЕНИЕ 4.2

Таблица 2 – Расширенная матрица следования с указанием весов дуг и вершин (SDR) данного ИЛГ.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40	41	42	43	44
1																																													3
2																																													1
3																																													4
4	1	4	2																																										2
5				6																																									4
6				6																																									5
7				8																																									5
8				2																																									3
9				2																																									7
10				6																																									7
11				1																																									7
12					3																																								1
13							2																																						7
14								1																																					2
15										5																																			2
16										5																																			1
17										5																																			3
18											8																																		8
19						2						5																																	3
20													4																																3
21									3					4				7																											3
22																			2																										8
23																			4																										2
24																			2																										4
25																				2																									4
26																				2																									2
27																				2																									2
28																				2																									2
29																				2																									2
30																				2																									2
31																				2																									2
32																				2																									2
33																					2																								2
34																					5																								4
35																						3																							3
36																						2																							5
37																																													7
38																																		1											4
39																																													5
40																																					1								1
41																																						4							5
42																																								6					2
43																																								6					5
44																																								3					7

ПРИЛОЖЕНИЕ 5.1