
- •Введение
- •Теоретическая часть
- •Понятие о современных вычислительных системах
- •1.2 Структура вс типа «Обобщенный nD-куб»
- •Основные определения, необходимые для разработки алгоритма распределения программных модулей по вычислительным модулям вычислительной сети
- •Распределение операторов по вм вычислительной системы с распределенной памятью для информационно-логической граф-схемы
- •3.1 Построение матрицы следования илг
- •3.2 Определение ранних сроков окончания выполнения операторов
- •3.3 Распределение нитей на структуре типа обобщенный гиперкуб
- •Заключение
- •Список используемой литературы
- •Алгоритм построения нитей
- •Алгоритм вычисления ранних сроков окончания выполнения операторов
- •Матрица дистанций для вс структуры гиперкуб 3*3*6.
- •Матрица дистанций для вс структуры гиперкуб 3*3*6 с размещением нитей по вм.
3.3 Распределение нитей на структуре типа обобщенный гиперкуб
По условию задан обобщенный трехмерный гиперкуб 3х3х6, на рисунке 21 для примера представлен гиперкуб 2х3х3.
Рисунок 21 - Схема представления обобщенного 3-х мерного гиперкуба 2х4х3
Для построения матрицы дистанций для гиперкуба необходимо перенумеровать его вершины. Нумерация показана в таблице 2:
Таблица 4 - Нумерация вершин гиперкуба.
Координата ВМ (x,y,z) |
000 |
001 |
002 |
003 |
004 |
010 |
011 |
012 |
013 |
014 |
020 |
021 |
022 |
023 |
024 |
Номер ВМ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Координата ВМ (x,y,z) |
030 |
031 |
032 |
033 |
034 |
040 |
041 |
042 |
043 |
044 |
100 |
101 |
102 |
103 |
104 |
Номер ВМ |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
Координата ВМ (x,y,z) |
110 |
111 |
112 |
113 |
114 |
120 |
121 |
122 |
123 |
124 |
130 |
131 |
132 |
133 |
134 |
Номер ВМ |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
Координата ВМ (x,y,z) |
140 |
141 |
142 |
143 |
144 |
200 |
201 |
202 |
203 |
204 |
210 |
211 |
212 |
213 |
214 |
Номер ВМ |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
Координата ВМ (x,y,z) |
220 |
221 |
222 |
223 |
224 |
230 |
231 |
232 |
233 |
234 |
240 |
241 |
242 |
243 |
244 |
Номер ВМ |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
Далее строится матрица дистанций, в которой расстояния указываются в минимальном числе промежуточных связей между соответствующими вычислительными модулями. В связи с большим размером матрицы дистанций, содержащей 5625 элементов (75х75), целиком она не приводится. Минимальную сумму расстояний до остальных модулей имеет 38-й модуль (это очевидно, так как данный модуль находится в геометрическом центре вычислительной системы). Сумма расстояний для него равна 230. Приведу часть матрицы дистанций для этого вычислительного модуля (см. таблицу 3):
Таблица 5 - Расстояния от 38-го вычислительного модуля до остальных ВМ.
Номер ВМ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
Расстояние |
5 |
4 |
3 |
4 |
5 |
4 |
3 |
2 |
3 |
4 |
3 |
2 |
1 |
2 |
3 |
Номер ВМ |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
Расстояние |
4 |
3 |
2 |
3 |
4 |
5 |
4 |
3 |
4 |
5 |
4 |
3 |
2 |
3 |
4 |
Номер ВМ |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
Расстояние |
3 |
2 |
1 |
2 |
3 |
2 |
1 |
0 |
1 |
2 |
3 |
2 |
1 |
2 |
3 |
Номер ВМ |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
Расстояние |
4 |
3 |
2 |
3 |
4 |
5 |
4 |
3 |
4 |
5 |
4 |
3 |
2 |
3 |
4 |
Номер ВМ |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
Расстояние |
3 |
2 |
1 |
2 |
3 |
4 |
3 |
2 |
3 |
4 |
5 |
4 |
3 |
4 |
5 |
Необходимо отметить, что сумма расстояний
от выбранного модуля до остальных может
быть получена аналитически, без нахождения
расстояний до каждого отдельного
вычислительного модуля. Рассмотрим
пример трёхмерного гиперкуба,
соответствующий решаемой задаче. Пусть
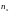 ,
,
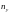 ,
,
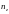 - число вычислительных модулей по осям
x, y
и z соответственно,
- число вычислительных модулей по осям
x, y
и z соответственно,
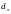 ,
,
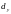 ,
,
 - размер гиперкуба по осям x,
y и z
соответственно,
- размер гиперкуба по осям x,
y и z
соответственно,
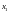 ,
,
 ,
,
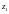 - координаты выбранного вычислительного
модуля. Тогда число вычислительных
модулей по осям x, y
и z, расположенных на
одинаковом расстоянии от выбранного,
равно соответственно:
- координаты выбранного вычислительного
модуля. Тогда число вычислительных
модулей по осям x, y
и z, расположенных на
одинаковом расстоянии от выбранного,
равно соответственно:
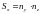 ,
,
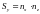 ,
,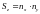 .
.
Тогда сумма всех расстояний будет равна:
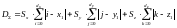 .(1)
.(1)
Для 38-го вычислительного модуля согласно
формуле (1) сумма расстояний:
 ,
что совпадает с полученным результатом.
,
что совпадает с полученным результатом.
Таким образом, оптимальным для размещения первой нити является 38-й вычислительный модуль. Для размещения всех нитей необходимо 10 вычислительных модулей. 38-й вычислительный модуль связан с 6 другими модулями. Таким образом, 6 нитей загружаются в 13-й, 33-й, 37-й, 38-й, 39-й, 43-й и 63-й вычислительные модули, а оставшиеся 3 – в 32-й, 34-й и 42-й модули (см рисунок 10), так как расстояние до 38-го ВМ до этих модулей равно 2:
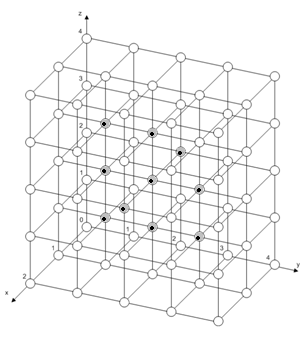
Рисунок 22 - Распределение нитей по вычислительным модулям ВС структуры «обобщенный гиперкуб».
