
- •Введение
- •Теоретическая часть
- •Понятие о современных вычислительных системах
- •1.2 Структура вс типа «Обобщенный nD-куб»
- •Основные определения, необходимые для разработки алгоритма распределения программных модулей по вычислительным модулям вычислительной сети
- •Распределение операторов по вм вычислительной системы с распределенной памятью для информационно-логической граф-схемы
- •3.1 Построение матрицы следования илг
- •3.2 Определение ранних сроков окончания выполнения операторов
- •3.3 Распределение нитей на структуре типа обобщенный гиперкуб
- •Заключение
- •Список используемой литературы
- •Алгоритм построения нитей
- •Алгоритм вычисления ранних сроков окончания выполнения операторов
- •Матрица дистанций для вс структуры гиперкуб 3*3*6.
- •Матрица дистанций для вс структуры гиперкуб 3*3*6 с размещением нитей по вм.
3.1 Построение матрицы следования илг
Основным инструментом анализа граф-схем алгоритмов служит матрица следования, а также различные её модификации. Матрица следования – это транспонированная матрица смежности. Использование матрицы следования вместо матриц смежности объясняется удобством размещения и анализа граф-схем.
Для удобства присвоим постоянный
идентификатор – Si i {1,
2. …, n}.Матрица S – квадратная – количество
строк и столбцов совпадает с количеством
вершин граф-cхемы. В матрица S i – ой
вершине графа G ставятся в соответствие
i – ые столбец и строка этой матрицы.
Если существует связь по управлению:
{1,
2. …, n}.Матрица S – квадратная – количество
строк и столбцов совпадает с количеством
вершин граф-cхемы. В матрица S i – ой
вершине графа G ставятся в соответствие
i – ые столбец и строка этой матрицы.
Если существует связь по управлению:
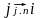 ,
то элемент матрицы равен (i,j) = j.n, при j
→ i образуется (i,j) = 1. Остальные элементы
матрицы S равны 0.
,
то элемент матрицы равен (i,j) = j.n, при j
→ i образуется (i,j) = 1. Остальные элементы
матрицы S равны 0.
Для заданной матрицы Si размера m отражения весов вершин вводится понятие расширенной матрицы следования SRi: прибавляется дополнительно k столбцов с номерами m+1, …, m+k, где k – размерность вектора весов вершин граф – схемы.
Построим расширенные матрицы следования для нашей граф – схемы. (Таблица 1 Приложение 4.1).
Построим матрицу следования с указанием весов дуг и вершин (SDR) для данной ИЛГ (Таблица 2 Приложение 4.2).
3.2 Определение ранних сроков окончания выполнения операторов
При исследовании граф-схем алгоритмов одними из основных характеристик являются ранние сроки окончания выполнения операторов. Имея эти величины, можно построить планы выполнения операторов с учётом распределения операторов по ВМ. Необходимо подчеркнуть, что на основе граф-схемы алгоритма, можно определить:
1) Частичную упорядоченность выполнения алгоритма.
2) Веса операторов pj, j = 1, …, m (обычно – времена выполнения процедур).
3) Началом отсчёта времени решения задачи является начало выполнения операторов, являющихся входами в алгоритм.
4) Тк – это путь максимальной длины в граф-схеме ( это максимальное время, за которое может быть решена данная задача).
Ранний срок окончания выполнения
оператора – это время на оси отсчёта
времени, равное t1, j =
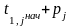 ,
j = 1 . . .m, где
,
j = 1 . . .m, где
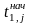 –
время начала выполнения j-ого оператора,
pj – время выполнения j-ого оператора,
полученное при минимальном времени
решения задачи Т=Тк.
–
время начала выполнения j-ого оператора,
pj – время выполнения j-ого оператора,
полученное при минимальном времени
решения задачи Т=Тк.
Каждая строка диаграммы может служить нитью для загрузки в процессор. Таким образом, получилось 7 нитей:
T1={3,4,5,12,19,23,38}
T2={2,6,16,24}
T3={1,7,13,20,27~34}
T4={8,14,21,35,39,43}
T5={9,17,36,42}
T6={10,15,38,41}
T7={11,18,22,37,40,44}
Tак как рассматривается ВС с общей памятью, обмена данными через каналы связи между процессорами нет, и количество нитей меньше, чем число процессоров, поэтому распределение нитей между ВМ может осуществляться, например, следующим образом: первая нить загружается в первый ВМ, вторая – во второй и т. д.
По алгоритму, приведенному в Приложении 2, определим ранние сроки окончания выполнения операторов и построим их диаграмму.
Учёт времён передачи информации
осуществляется, используя следующие
соотношения: для развёртки– p,j=qi,j+pj,
где j= –
номера операторов, образующих
развёртку; для свёртки– pj=
qj,i
+pj
где j=
–
номера операторов, образующих cвёртку.
С помощью матрицы следования с указанными
весами дуг и вершин модифицированные
веса вершин можно вычислить следующим
образом: если в i-й строке
найдено одно число, то вес i-й
вершины модифицируется к виду: рi:=pi+qji;
если в i-й строке
найдено несколько чисел, то веса вершин
модифицируются к виду рj:=pj+qi,j,
j={
},
где j – номера столбцов,
в которых найдены числа, qi,j
– множество весов дуг, принадлежащих
i-й строке.
–
номера операторов, образующих
развёртку; для свёртки– pj=
qj,i
+pj
где j=
–
номера операторов, образующих cвёртку.
С помощью матрицы следования с указанными
весами дуг и вершин модифицированные
веса вершин можно вычислить следующим
образом: если в i-й строке
найдено одно число, то вес i-й
вершины модифицируется к виду: рi:=pi+qji;
если в i-й строке
найдено несколько чисел, то веса вершин
модифицируются к виду рj:=pj+qi,j,
j={
},
где j – номера столбцов,
в которых найдены числа, qi,j
– множество весов дуг, принадлежащих
i-й строке.
Таблица 3- Ранние сроки окончания выполнения операторов
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
|||||||
T |
3 |
1 |
4 |
6 |
10 |
11 |
11 |
9 |
13 |
13 |
13 |
11 |
18 |
11 |
15 |
14 |
16 |
21 |
|||||||
№ |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26-33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
||||||
Т |
14 |
21 |
16 |
29 |
16 |
18 |
18 |
37 |
20 |
19 |
34 |
36 |
22 |
25 |
35 |
41 |
37 |
40 |
42 |
||||||
После того, как ы определили ранние сроки выполнения операторов, постоим диаграммы ранних сроков выполнения данных операторов.



Рисунок 5 - Диаграмма ранних сроков окончания выполнения операторов
Паузы, возникшие на 2, 16, 19, 20 моментах времени связаны с синхронизацией вычислений, определяемой структурой рассматриваемой граф-схемы. Общее время решения этой задачи составляет 42 условных единиц.
Анализируя представленный способ построения плана решения задач на ВС, можно сделать вывод, что достаточно простыми средствами можно построить достаточно эффективную процедуру организации решения параллельных задач на ВС.
При построении временных диаграмм выполнения операторов необходимо учитывать, что они строятся для информационно-логической граф-схемы, и не все операторы будут выполнены. Это можно сделать, например, с помощью динамического плана, состояние которого изменяется каждый раз, как только выполняется очередной логический оператор.
Для рассматриваемой граф-схемы временные диаграммы будут выглядеть, как показано на рисунках 4-9:


Рисунок 6 – Временная диаграмма при срабатывании дуги 4.1 и 19.1

Рисунок 7 – Временная диаграмма при срабатывании дуги 4.1 и 19.2

Рисунок 8 – Временная диаграмма при срабатывании дуги 4.1 и 19.3

Рисунок 9 – Временная диаграмма при срабатывании дуги 4.2 и 19.1

Рисунок 10 – Временная диаграмма при срабатывании дуги 4.2 и 19.2

Рисунок 11 – Временная диаграмма при срабатывании дуги 4.2 и 19.3


Рисунок 12 – Временная диаграмма при срабатывании дуги 4.3

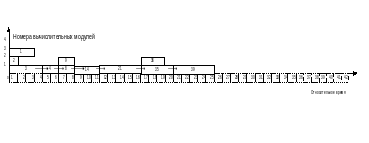
Рисунок 13 – Временная диаграмма при срабатывании дуги 4.4 и 4.5

Рисунок 14 – Временная диаграмма при срабатывании дуги 4.6 и 10.1

Рисунок 15 – Временная диаграмма при срабатывании дуги 4.6 и 10.2

Рисунок 16 – Временная диаграмма при срабатывании дуги 4.6 и 10.3

Рисунок 17 – Временная диаграмма при срабатывании дуги 4.7, 22.1 и 40.1

Рисунок 18 – Временная диаграмма при срабатывании дуги 4.7, 22.1 и 40.2

Рисунок 19 – Временная диаграмма при срабатывании дуги 4.7, 22.1 и 40.3
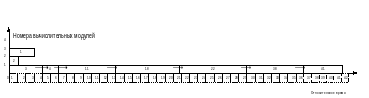
Рисунок 20 – Временная диаграмма при срабатывании дуги 4.7 и 22.2
Как видно из рисунков 6-20, максимальное число нитей для данного алгоритма равно 8.
