7. Системы дифференциальных уравнений

7.1 Нормальная система дифференциальных уравнений

Нормальная система двух дифференциальных уравнений 1 порядка с двумя неизвестными имеет вид

где - аргумент; - искомые функций.

Порядок системы определяется числом входящих в неё уравнений;

Система– нормальная система II порядка.

Совокупность функций

определенных и непрерывно дифференцируемых в интервале , называется решением системы в этом интервале, если она обращает в тождество каждое уравнение системы:

Нормальная система II порядка допускает общее решение, содержащее две произвольных постоянных:

Решение, удовлетворяющее начальным условиям

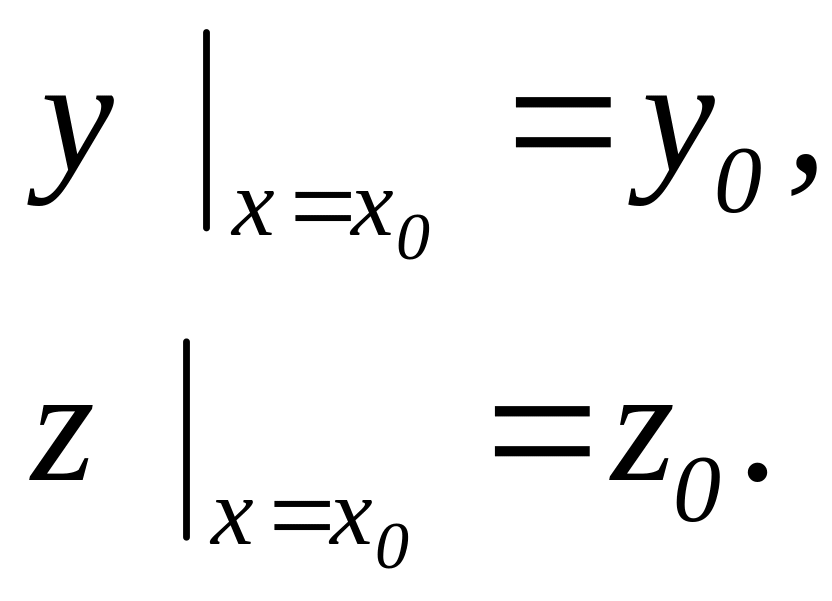называется частным решением системы.

Пример 7.1.1. Найти общее решение системы дифференциальных уравнений

Имеем простейший случай, когда одно из уравнений – второе – содержит только одну искомую функцию. Решим его:

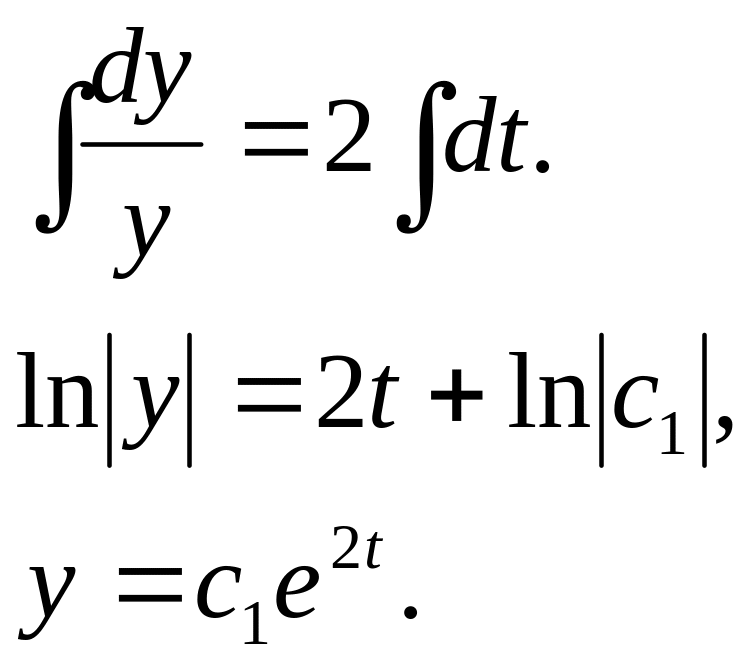
Подставим полученную функцию в первое уравнение системы:

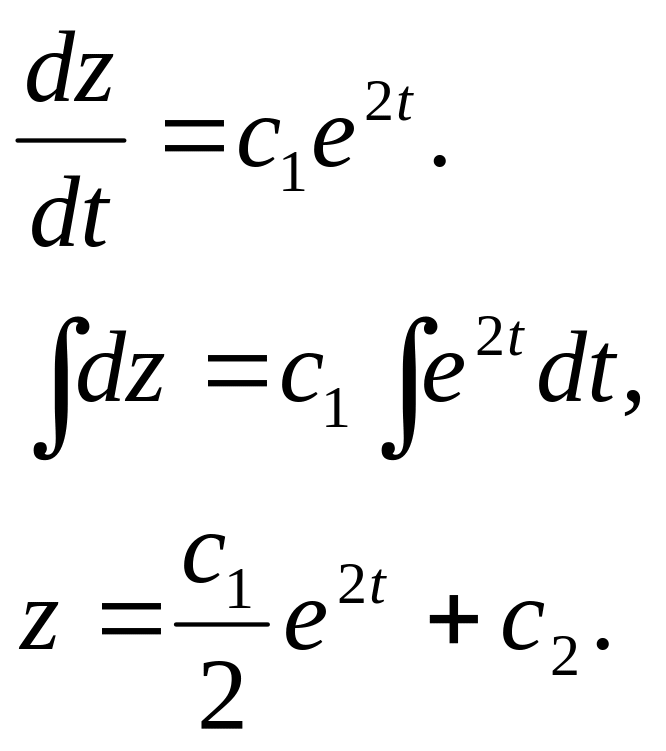
Ответ:

Пример 7.1.2. Найти общее решение системы дифференциальных уравнений

Ответ:

В общем случае нормальная система II порядка решается сведением её к равносильному уравнению II порядка относительно одной из искомых функций.

Пример 7.1.3. Найти частное решение системы дифференциальных уравнений

1⁰. Продифференцируем одно из уравнений системы.

Например, если мы хотим свести систему к равносильному её уравнению II порядка относительно функции у, необходимо продифференцировать первое уравнение системы:

(а)

2⁰. Выразим из данной системы функцию и её производную

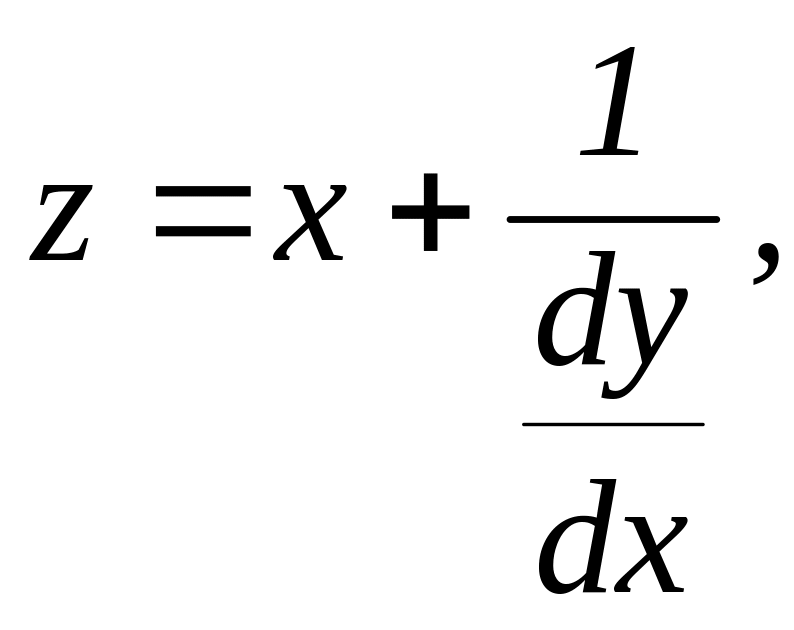(б)

3⁰. Подставим функцию и её производную в уравнение (а):

.

4⁰. Решим уравнение (а)

- уравнение II порядка, допускающее понижение подстановкой ;

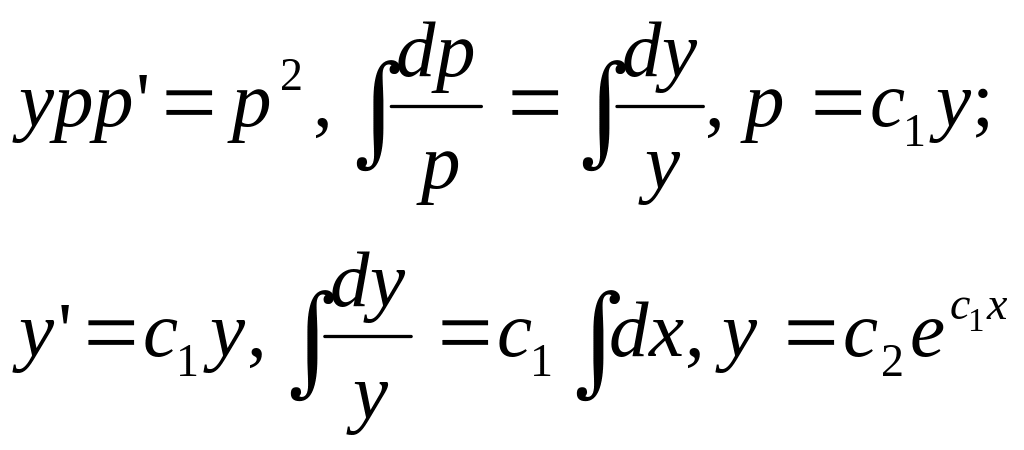
5⁰. Найдём функцию по формуле (б):

.

6⁰. Запишем общее решение системы:

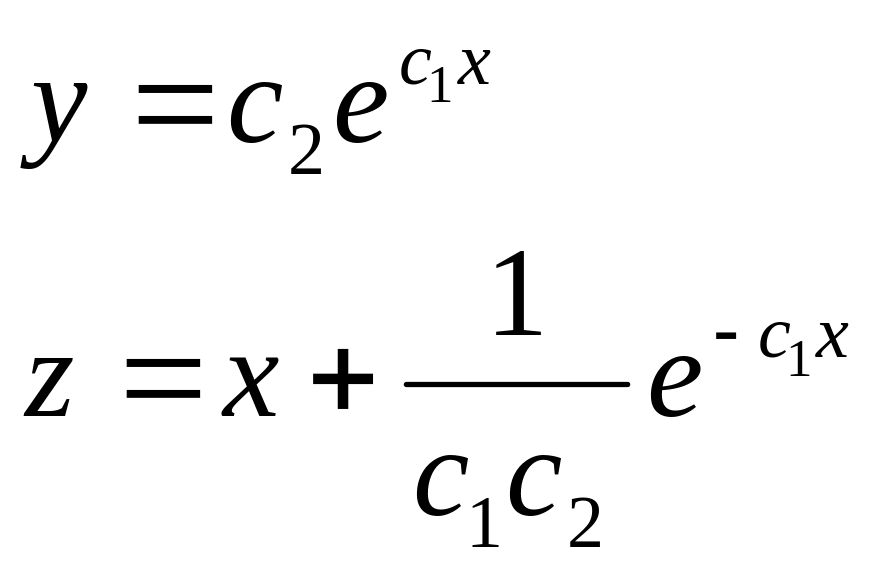
7⁰. Найдём произвольные постоянные:

При имеем

.

8⁰. Запишем ответ:

Модуль 10. Кратные интегралы

1. Двойной интеграл

1.1. Объём цилиндрического тела

Цилиндрическим телом называется тело, ограниченное плоскостью Оху, поверхностью, с которой любая прямая, параллельная оси Oz, пересекается не более чем в одной точке, и цилиндрической поверхностью, образующая которой параллельна оси Oz.

Область D, высекаемая в плоскости Оху цилиндрической поверхностью, называется основанием цилиндрического тела (см. рис.1). В частных случаях боковая цилиндрическая поверхность может и отсутствовать, примером тому служит тело, ограниченное плоскостью Оху и верхней полусферой .

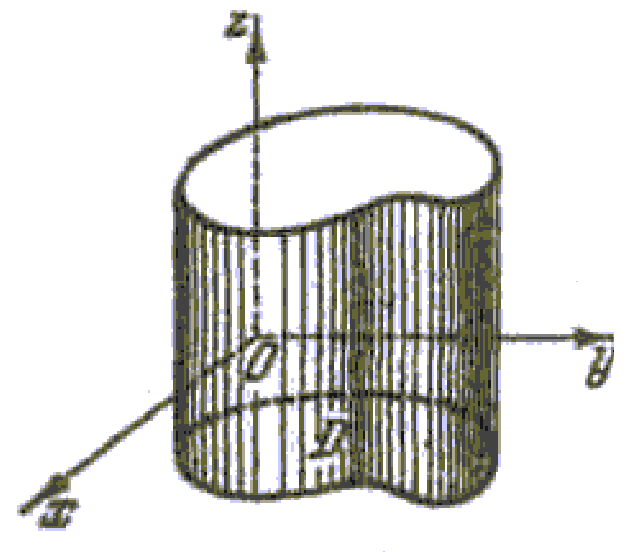
Рис.1

Обычно тело можно составить из некоторого числа цилиндрических тел и определяют искомый объект как сумму объёмов цилиндрических тел, составляющих это тело.

Прежде всего напомним два принципа, из которых мы исходим при определении объёма тела:

1) если разбить тело на части, то его объем будет равен сумме объёмов всех частей;

2) объём прямого цилиндра, т.е. цилиндрического тела, ограниченного плоскостью, параллельной плоскости Оху, равен площади основания, умноженной на высоту тела.

Пусть z = f(x, y) есть уравнение поверхности, ограничивающей цилиндрическое тело. Будем считать функцию f(x, y) непрерывной в области D и сначала предположим, что поверхность целиком лежит над плоскостью Оху, т.е. что f(x, y) > 0 всюду в области D.

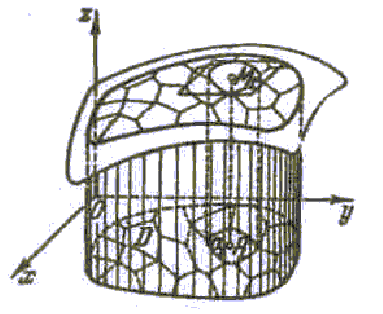
Рис.2

Обозначим искомый объём цилиндрического тела через V. Разобьём основание цилиндрического тела – область D – на некоторое число n областей произвольной формы; будем называть их частичными областями. Пронумеровав частичные области в каком-нибудь порядке, обозначим их через σ₁ σ₂,…, σ_n, а их площади – через Δ σ₁ Δ σ ₂ ,…, Δ σ _n. Через границу каждой частичной области проведем цилиндрическую поверхность с образующей, параллельной оси Oz. Эти цилиндрические поверхности разрежут поверхность на n кусков, соответствующих n частичным областям. Таким образом, цилиндрическое тело окажется разбитым на n частичных цилиндрических тел (см. рис.2). Выберем в каждой частичной области σ_i произвольную точку P_i (x_i, y_i) и заменим соответствующее частичное цилиндрическое тело прямым цилиндром с тем же основанием и высотой, равной z_i = f (x_i y_i). В результате получим n-ступенчатое тело, объём которого равен .

Принимая объём V данного цилиндрического тела приближенно равным объёму построенного n-ступенчатого тела, будем считать, что V_n тем точнее выражает V, чем больше n и чем меньше каждая из частичных областей. Переходя к пределу при , мы будем требовать, чтобы не только площадь каждой частичной области стремилась к нулю, но чтобы стремились к нулю все её размеры. Если назвать диаметром области наибольшее расстояние между точками ее границы (например, диаметр прямоугольника равен его диагонали, диаметр эллипса – его большой оси. Для круга приведённое определение диаметра равносильно обычному), то высказанное требование будет означать, что каждый из диаметров частичных областей должен стремиться к нулю; при этом сами области будут стягиваться в точку.

Замечание.

Если известно только, что площадь области стремится к нулю, то эта область может и не стягиваться в точку. Например, площадь прямоугольника с постоянным основанием и высотой, стремящейся к нулю, стремится к нулю, а прямоугольник стягивается к своему основанию, т.е. к отрезку.

В соответствии со сказанным мы принимаем искомый объем V равным пределу, к которому стремится V_n при стремлении к нулю наибольшего диаметра частичных областей (при этом ):

.

К отысканию предела подобных сумм для функций двух переменных приводят самые разнообразные задачи, а не только задача об объеме.

Рассмотрим этот вопрос в общем виде. Пусть f(x, y) – любая функция двух переменных (не обязательно положительная), непрерывная в некоторой области D, ограниченной замкнутой линией. Разобьём область D на частичные, как указано выше, выберем в каждой частичной области по произвольной точке P_i (x_i , y_i) и составим сумму

, (1)

где f (x_i , y_i) – значение функции в точке P_i ; и Δσ_ι – площадь частичной области.

Сумма (1) называется n–й интегральной суммой для функции f(x, y) в области D, соответствующей данному разбиению этой области на n частичных областей.

Определение. Двойным интегралом от функции f(x, y) по области D называется предел, к которому стремится n-я интегральная сумма при стремлении к нулю наибольшего диаметра частичных областей.

Записывается это так:

.

Читается: «двойной интеграл от f(x, y) на dσ по области D». Выражение f(x, y) dσ, показывающее вид суммируемых слагаемых, называется подынтегральным выражением; функция f(x, y) называется подынтегральной функцией, dσ – элементом площади, область D – областью интегрирования, наконец, переменные x и у называются переменными интегрирования.

Таким образом, можно сказать, что объём цилиндрического тела, ограниченного плоскостью Оху, поверхностью z = f(x, y) (f(x, y) > 0) и цилиндрической поверхностью с образующей, параллельной оси Oz, выражается двойным интегралом от функции f(x, y), взятым по области, являющейся основанием цилиндрического тела:

.

Аналогично теореме существования обыкновенного интеграла имеет место следующая теорема.

Теорема существования двойного интеграла.

Если функция f(x, y) непрерывна в области D, ограниченной замкнутой линией, то её n-я интегральная сумма стремится к пределу при стремлении к нулю наибольшего диаметра частичных областей.

Этот предел, т.е. двойной интеграл , не зависит от способа разбиения области D на частичные области σ, и от выбора в них точек Р_i.

Перечислим свойства двойного интеграла, считая подынтегральные функции интегрируемыми.

Свойство 1. , с – const.

Свойство 2. .

Свойство 3. Если область D разбить линией на две области D₁ и D₂ такие, что D₁  D₂ = D, а пересечение D₁ и D₂ состоит лишь из линии, разделяющей, то

.

Свойство 4. Если в области D имеет место неравенство f(x, y)  0, то и .

Свойство 5. , так как .

Свойство 6. Если функция f(x, y) непрерывна в замкнутой области D, площадь которой S, то , где m M – соответственно наименьшее и наибольшее значения подынтегральной функции в области D.

Свойство 7. Если функция f(x, y) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка (x₀; y₀), что . Величину называют средним значением функции f(x, y) в области D.

Двойной интеграл, разумеется, представляет собой число, зависящее только от подынтегральной функции и области интегрирова0ния и вовсе не зависящее от обозначений переменных интегрирования, так что, например,

Далее мы убедимся в том, что вычисление двойного интеграла может быть произведено посредством двух обыкновенных интегрирований.