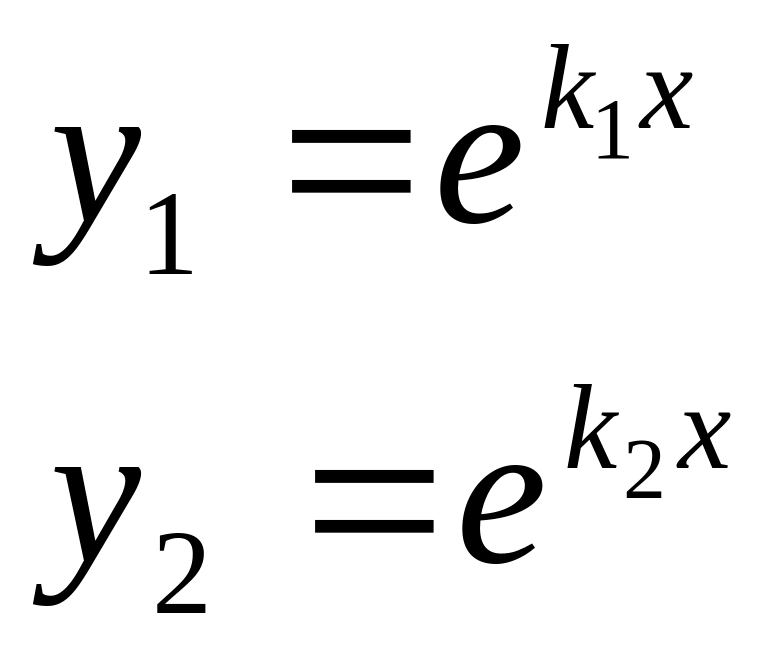- •Теоретический материал по высшей математике
- •Часть III
- •Модуль 9. Дифференциальные уравнения
- •1. Дифференциальные уравнения I порядка. Уравнения с разделяющимися переменными
- •1.1. Дифференциальные уравнения I порядка. Общие понятия
- •1.2. Дифференциальные уравнения с разделяющимися переменными
- •2. Однородные дифференциальные уравнения. Уравнения в полных дифференциалах
- •2.1. Однородные дифференциальные уравнения I порядка
- •2.2. Уравнения в полных дифференциалах
- •3. Линейные дифференциальные уравнения порядка. Уравнения Бернулли
- •3.1. Линейные дифференциальные уравнения порядка
- •3.2. Уравнения Бернулли
- •4. Дифференциальные уравнения порядка, допускающие понижение порядка
- •4.1. Дифференциальные уравнения порядка. Общие понятия
- •4.2. Уравнения порядка, допускающие понижение порядка
- •5. Линейные дифференциальные уравнения порядка коэффициентами
- •5.1. Однородные линейные уравнения порядка с постоянными коэффициентами
- •5.2. Неоднородные линейные уравнения іі порядка с постоянными коэффициентами. Метод Эйлера вариации произвольных постоянных
- •6. Линейные неоднородные уравнения іі порядка с постоянными коэффициентами. Метод Лагранжа неопределенных коэффициентов
- •7. Системы дифференциальных уравнений
- •7.1 Нормальная система дифференциальных уравнений
- •Модуль 10. Кратные интегралы
- •1. Двойной интеграл
- •1.1. Объём цилиндрического тела
- •1.2. Вычисление двойных интегралов в декартовых координатах
- •1.3. Вычисление двойных интегралов в полярных координатах
- •1.4. Приложения двойных интегралов к задачам механики
- •1.5. Вычисление площадей и объёмов с помощью двойных интегралов.
- •1.6. Вычисление площади поверхности.
- •2. Тройной интеграл
- •2.1. Масса неоднородного тела
- •2.2. Вычисление тройных интегралов в декартовых координатах.
- •2.3. Вычисления тройных интегралов в цилиндрических координатах.
- •2.4. Вычисление тройных интегралов в сферических координатах
- •2.5. Приложение тройных интегралов.
- •Модуль 11. Криволинейные и поверхностные интегралы
- •1. Криволинейные интегралы
- •1.1. Криволинейный интеграл первого типа (по длине дуги)
- •1.2. Криволинейный интеграл второго типа (по координатам)
- •1.3. Формула Грина
- •1.4. Условия независимости криволинейного интеграла от пути интегрирования
- •1.5. Связь между криволинейными интегралами первого и второго типов
- •2. Поверхностные интегралы
- •2.1. Поверхностные интегралы первого типа
- •2.2. Понятие двухсторонней поверхности. Ориентация поверхности
- •2.3. Поверхностный интеграл второго типа (по проекциям)
- •2.4. Связь поверхностных интегралов I и II типов
- •2.5. Формула Остроградского
- •3. Основные понятия теории поля
- •Список литературы
- •Часть III
5. Линейные дифференциальные уравнения порядка коэффициентами
5.1. Однородные линейные уравнения порядка с постоянными коэффициентами
Однородное линейное уравнение порядка с постоянными коэффициентами имеет вид
![]() , где
, где ![]() - заданные числа.
- заданные числа.
Структура решения уравнения (5.1) определяется следующими теоремами.
Теорема 5.1. Всякое линейное однородное уравнение порядка имеет систему двух линейно независимых частных решений.
![]()
![]() .
.
Эта система носит название фундаментальной системы решений.
Теорема 5.2. (о структуре решения)
Общее решение линейного однородного
уравнения порядка
есть линейная комбинация частных решений
его фундаментальной системы:
![]() .
.
Для отыскания фундаментальной системы
решений составляют так называемое
характеристическое уравнение
![]() .
.
В зависимости от вида корней (вещественные различные, вещественные равные, комплексные) фундаментальная система решений имеет различный вид (табл. 3).
Виды фундаментальной системы решений линейного однородного уравнения
Таблица 3
Дискриминант характеристического уравнения |
Корни характеристического уравнения |
Фундаментальная система частных решений |
Общее решение |
|
вещественные различные
|
|
|
|
вещественные равные
|
|
|
|
Комплексные
|
|
|
Пример 5.1.1. Найти решение задачи Коши для дифференциального уравнения
![]() ,
удовлетворяющее начальным условиям
,
удовлетворяющее начальным условиям
![]()
10. Определим тип уравнения.
- линейное, однородное ІІ порядка, с постоянными коэффициентами.
20. Запишем формулу общего решения:
30. Составим и решим характеристическое уравнение:
![]()
![]()
(корни вещественные, различные)
40. Запишем фундаментальную систему решений:
![]() .
.
50. Запишем общее решение уравнения:
![]()
60. Найдём значения произвольных
постоянных
и
![]() :
:
![]()
При
![]() получаем
получаем
![]()
70. Запишем ответ – частное решение уравнения:
![]() .
.
Пример 5.1.2. Найти общее решение
дифференциального уравнения
![]() .
.
10. Определим тип уравнения.
- линейное, однородное, ІІ порядка, с постоянными коэффициентами
20. Запишем формулу общего решения:
.
30. Составим и решим характеристическое уравнение:
![]()
(корни вещественные, равные).
40. Запишем фундаментальную систему решений:
![]() .
.
50. Запишем общее решение уравнения:
![]()
Пример 5.1.3. Найти решение задачи
Коши для дифференциального уравнения
![]() ,
,
удовлетворяющее начальным условиям
![]() .
.
10. Определим тип уравнения.
- линейное, однородное, ІІ порядка, с постоянными коэффициентами
20. Запишем формулу общего решения:
.
30. Составим и решим характеристическое уравнение:
![]()
(корни комплексные).
40. Запишем фундаментальную систему решений:
![]() .
.
50. Запишем общее решение уравнения:
![]()
60. Найдём значения произвольных постоянных и :
![]()
При
![]() получаем
получаем
![]()
70. Запишем ответ – частное решение уравнения:
![]() .
.
Пример 5.1.4. Найти общее решение дифференциальных уравнений:
а)![]() ; г)
; г)
![]() ;
;
б)
![]() ; д)
; д)
![]() ;
;
в)![]() ; е)
; е)
![]() .
.
Ответ: а)
![]() ;
;
б)![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)![]() .
.