2.2. Уравнения в полных дифференциалах
Уравнение
называется уравнением в полных
дифференциалах, если его левая часть
– полный дифференциал некоторой функции
,
т.е.
.
Необходимым и достаточным условием
полного дифференциала является равенство
частных производных
.
Общий интеграл уравнения в полных
дифференциалах имеет вид
,
где функция может быть найдена по одной из формул:
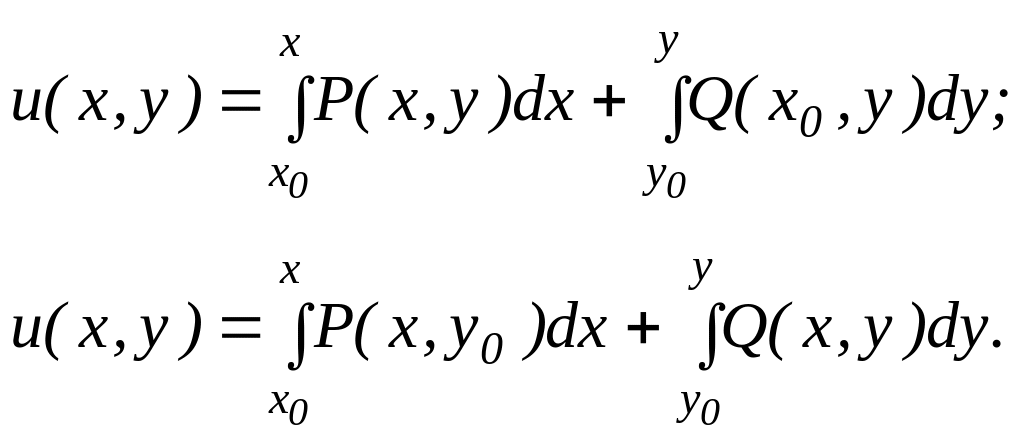
Пример 2.2.1. Указать уравнения в полных дифференциалах:
а)
10. Дифференциальное уравнение записано в симметричной форме, где
,
20. Найдём частные производные:
,
.
30. Сравним частные производные. Так как , то уравнение является уравнением в полных дифференциалах.
б)
10. Дифференциальное уравнение записано в симметричной форме, где
,
20. Найдём частные производные:
,
.
30. Сравним частные производные. Так как , то уравнение является уравнением в полных дифференциалах.
Пример 2.2.2. Найти общий интеграл дифференциального уравнения
.
10. Определим тип уравнения (таблица 1):
Запишем уравнение в симметричной форме:
,
,
,
тогда
,
1.2. Найдём частные производные:
,
.
1.3. Сравним частные производные. Так как
,
то уравнение является уравнением в
полных дифференциалах.
20. Запишем формулу общего интеграла:
30. Выберем формулу для отыскания функции :
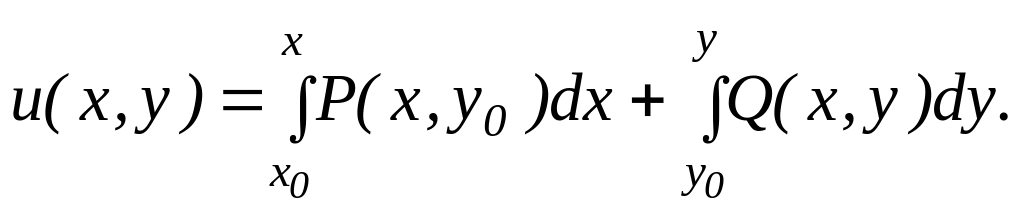
40. Найдём функцию :
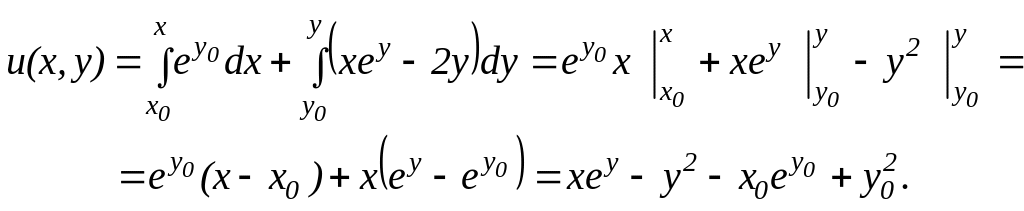
50. Запишем общий интеграл уравнения:
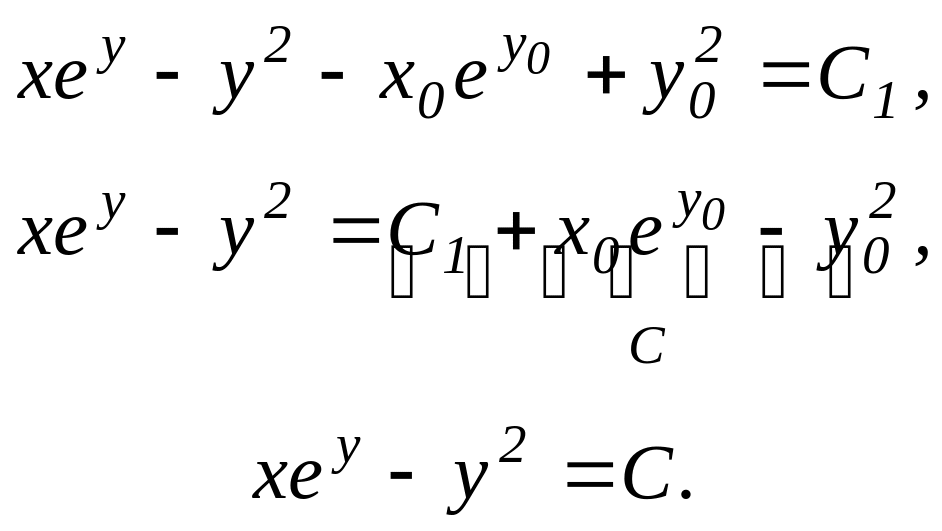
Пример 2.2.3. Найти общий интеграл дифференциального уравнения
Ответ:
Пример 2.2.4. Найти решение задачи Коши для дифференциального уравнения
удовлетворяющее
начальным условиям
10. Определим тип уравнения (таблица 1):
1.1 Дифференциальное уравнение записано в симметричной форме, где
,
1.2. Найдём частные производные:
,
.
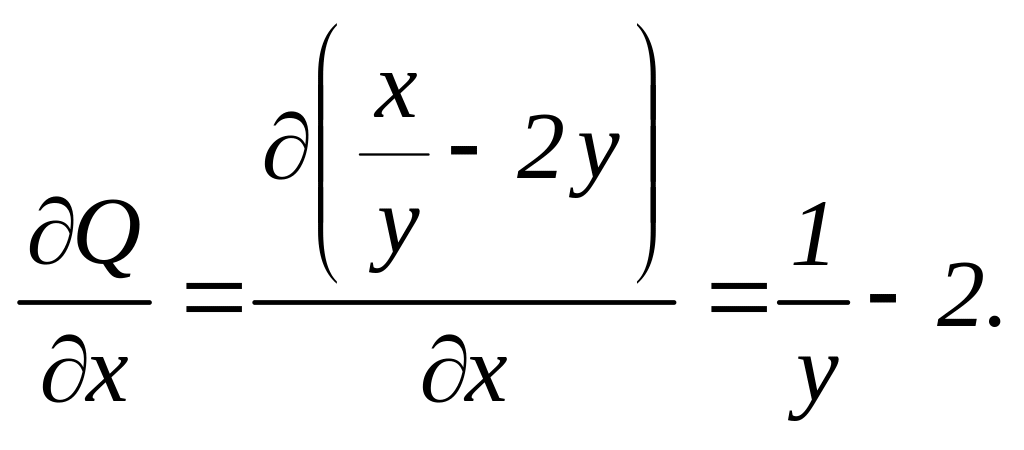1.3. Сравним частные производные. Так как
,
то уравнение является уравнением в
полных дифференциалах.
20. Запишем формулу общего интеграла:
30. Выберем формулу для отыскания функции :
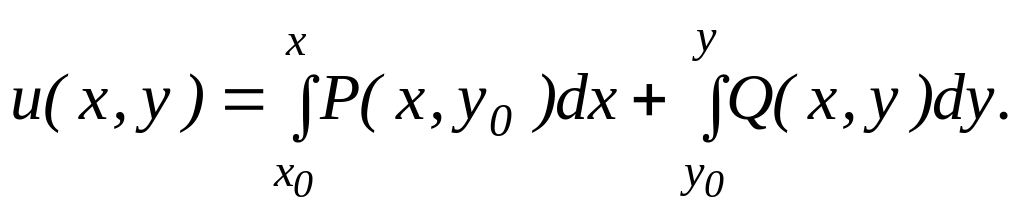
40. Найдём функцию :
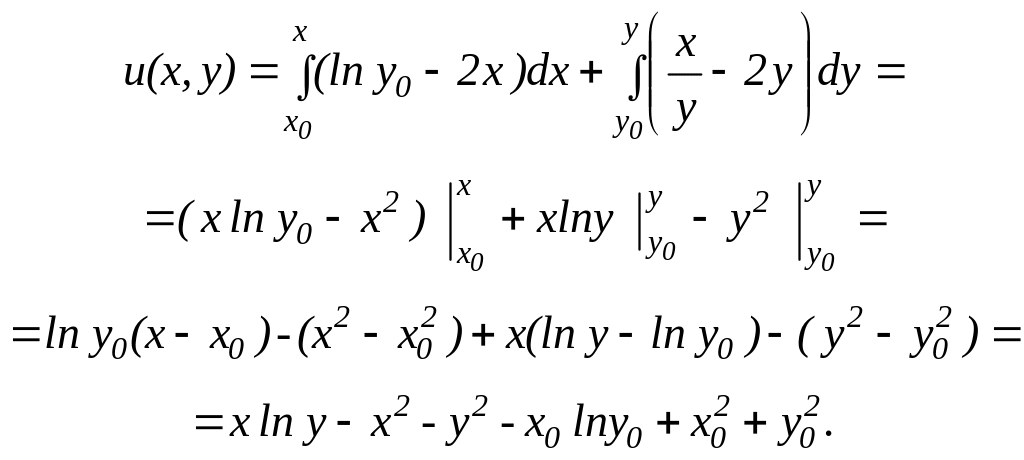
50. Запишем общий интеграл уравнения:
,
,
.
60. Найдём значение произвольной
постоянной. При
получим
,
.
60. Запишем ответ – частное решение уравнения:
Пример 2.2.5. Среди уравнений указать то, которое является одновременно и однородным, и в полных дифференциалах:
а)
б)
в)
3. Линейные дифференциальные уравнения порядка. Уравнения Бернулли
3.1. Линейные дифференциальные уравнения порядка
Линейным дифференциальным уравнением порядка называется уравнение, линейное относительно функции и её производной:
-
уравнение, линейное относительно
;
-
уравнение, линейное относительно
.
Здесь
- заданные функции или константы. При
уравнение называется однородным, при
- неоднородным.
Пример 3.1.1. Определить тип уравнений:
а)
- линейное относительно
;
приводится к стандартной форме
,
где
,
.
б)
- линейное относительно
;
подстановкой
приводится к стандартной форме
,
где
,
.
Пример 3.1.2. Среди уравнений указать линейные:
а)
;
б)
;
в)
;
г)
.
Ответ: а) линейное относительно ;
б) не является линейным;
в) линейное относительно
;
г) линейное относительно .
Однородные линейные уравнения (Q=0) могут быть решены разделением переменных. Неоднородные линейные уравнения можно свести к последовательности двух уравнений с разделяющимися переменными подстановкой
.
Пример 3.1.3. Найти решение задачи Коши для дифференциального уравнения
,
удовлетворяющее начальным условиям
.
10. Определим тип уравнения (таблица 1). Приведём к стандартной форме записи делением на , получим:
- линейное уравнение относительно
функции
.
20. Запишем подстановку:
.
30. Осуществим подстановку в данное уравнение:
.
40. Запишем последовательность
уравнений относительно функций
и
.
Подстановка
позволяет одну из функций сомножителей
выбрать произвольно. Поступим так:
сгруппируем первый и третий (можно
второй и третий) члены уравнения
.
Выберем функцию так, чтобы она обращала в нуль скобку
Тогда функция должна удовлетворять условию
.
Итак, получили последовательность уравнений:
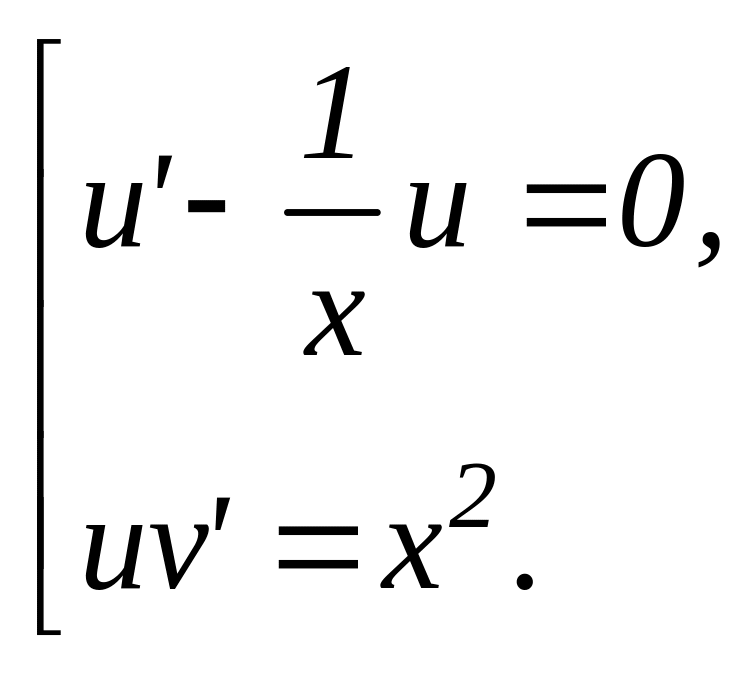
50. Найдём функции и .
Каждое из уравнений последовательности (пункт 40) является уравнением с разделяющимися переменными:
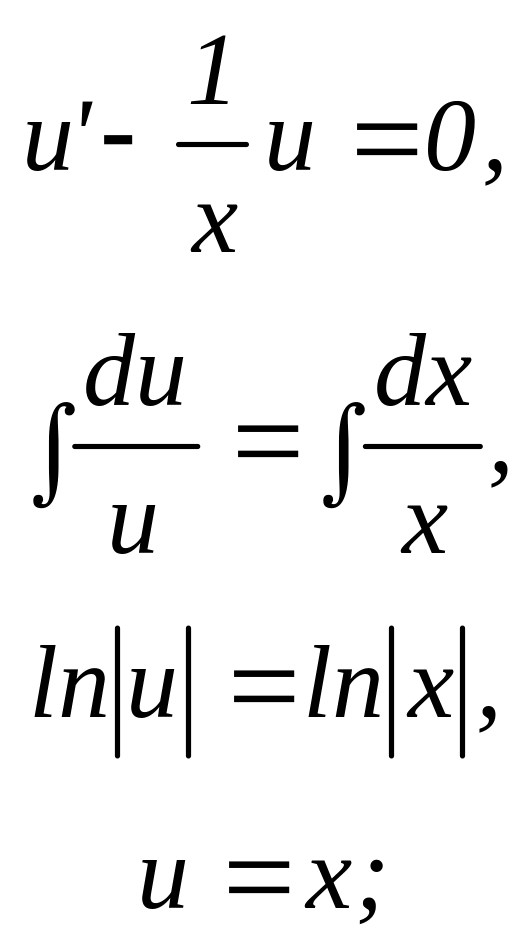
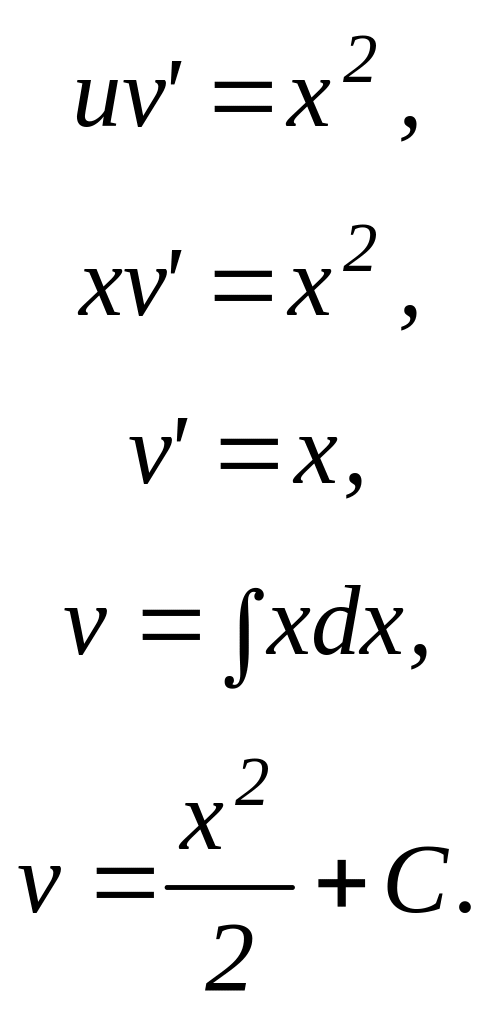
60. Запишем общее решение дифференциального уравнения:
.
70. Найдём значение произвольной постоянной.
При
получаем
.
80. Запишем ответ – частное решение уравнения:
.
Пример 3.1.4. Найти решение задачи Коши для дифференциального уравнения
удовлетворяющее начальным условиям
.
Ответ:
.
Пример 3.1.5. Найти общее решение дифференциального уравнения
.
Ответ:
.
Пример 3.1.6. Найти общее решение дифференциального уравнения
.
Ответ:
.
Пример 3.1.7. Найти общее решение дифференциального уравнения
.
10. Определим тип дифференциального уравнения (таблица 1):
- уравнение, линейное относительно функции .
20. Запишем подстановку:
.
30. Осуществим подстановку в данное уравнение:
.
40. Запишем последовательность уравнений относительно функций и . Сгруппируем первый и третий члены уравнения:
.
Выберем функцию так, чтобы она обращала в нуль скобку, получим последовательность уравнений:
50. Найдём функции и .
Каждое из уравнений последовательности (пункт 40) является уравнением с разделяющимися переменными:
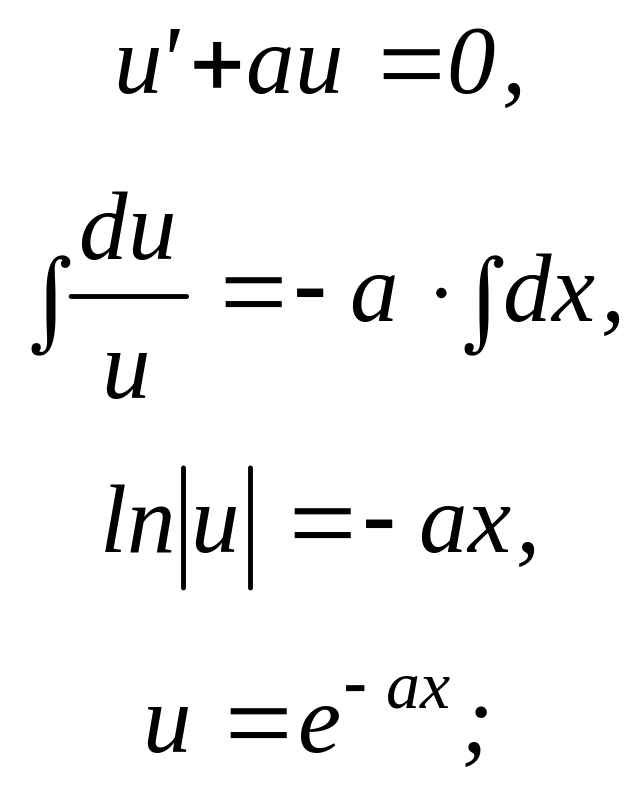
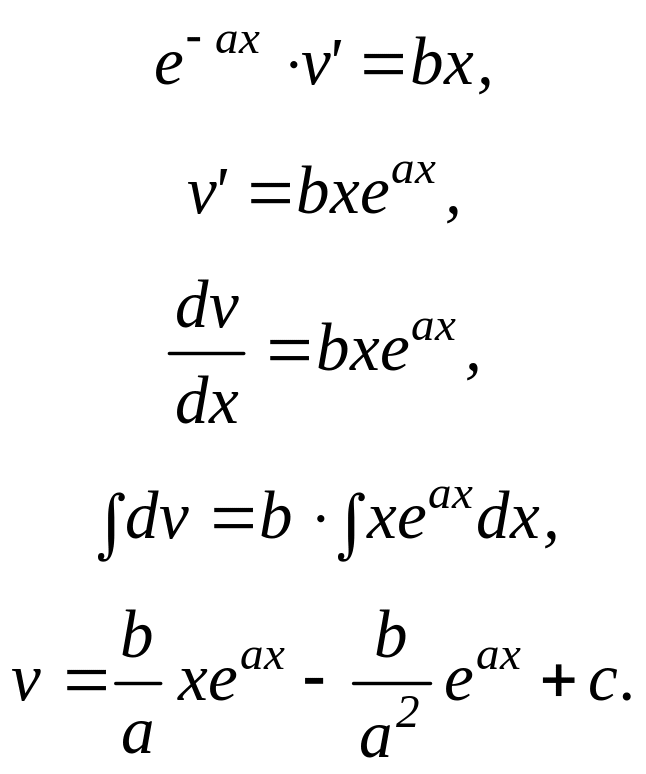
60. Запишем общее решение дифференциального уравнения:
