2.4. Связь поверхностных интегралов I и II типов

Напомним сначала, как найти координаты единичного вектора нормали, т.е. её направляющие косинусы, если поверхность задана уравнением F(x, y, z) = 0:

grad F(M)

(см. [2]), где М – какая-то точка поверхности.

Единичный вектор ,

,

.

Заметим, в частности, что если уравнение поверхности задано в виде z = f(x, y), от него легко перейти к уже рассмотренному случаю F(x, y, z) = f(x, y)  z = 0.

Дифференцируя полученное уравнение, находим координаты вектора нормали, а затем его длину:

, , ; ,

.

Теперь найдём проекции элемента поверхности d на каждую из координатных плоскостей:

Подставляя эти равенства в составной интеграл (7), получим формулу, связывающую поверхностные интегралы по поверхности  первого и второго типов:

= (11)

Пример 5. Вычислить

где  – часть плоскости (р) х + 2у + z = 4, вырезанная координатными плоскостями, по стороне, обращённой к началу координат.

Решение

Вариант 1. Вычислим поверхностный интеграл второго типа, переведя его в интеграл первого типа, для чего используем формулу (11). Из уравнения плоскости (р) х + 2у + z = 4 находим вектор нормали и его направляющие косинусы. Длина вектора По условию нормаль направлена в сторону начала координат, следовательно, все направляющие косинусы возьмём с отрицательным знаком:

Записываем формулу

Для вычисления поверхностного интеграла требуется выбрать одну из координатных плоскостей, например хоу, на которую проектируем плоскость (р) затем переводим поверхностный интеграл в двойной, заменив переменную z в подынтегральном выражении на z = 4 – x – 2y, соответственно вычислив d:

Cоставляем двойной интеграл по области D_xy

Ответ:

Вариант 2. Вычислим составной поверхностный интеграл второго типа как сумму трёх интегралов:

Направляющие косинусы найдены в предыдущем варианте решения, а, значит, при переходе к двойным интегралам по соответствующим координатам знак двойного интеграла будет отрицательным. Начнём с первого, спроектировав плоскость р на координатную плоскость yoz (см. рис. 14.16), в подынтегральном выражении заменим координату x = 4 – 2y – z.

Итак,

Чтобы вычислить I₂, проектируем плоскость (p) на xoz (см. рис. 117):

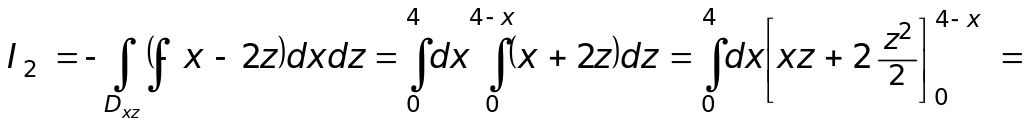
Для вычисления I₃ проектируем плоскость (p) на xoу (см. рис. 15) и заменяем лишнюю координату z = 4 – х – 2y, тогда

Итак,

Ответ:

2.5. Формула Остроградского

В теории криволинейных интегралов мы познакомились с формулой Грина, связывающей двойной интеграл по плоской области с криволинейным по контуру этой области. Её аналогом в теории поверхностных интегралов служит формула Остроградского, связывающая тройной интеграл по пространственной области Т с интегралом по поверхности, ограничивающей эту область.

Теорема. Если функции P(x, y, z), Q(x, y, z), R(x, y, z) непрерывны вместе со своими частными производными в области Т, то имеет место формула

.

Доказательство. Формулу (14.12) можно рассматривать как результат суммирования трёх интегралов:

,

,

.

Докажем равенство (15). Рассмотрим цилиндрическое тело Т ограниченное поверхностями

,

и цилиндром ₃ с образующими, параллельными оси oz.

Пусть D — область плоскости хоу, в которую проектируется тело Т, а функция R(x, y, z) определена в замкнутой области Т вместе со своей производной . Тогда

.

М ожно переходить к поверхностным интегралам по внешней стороне поверхности  (см. формулу для вычислений (14.8)), учитывая ориентацию поверхностей: нормаль к образует острый угол с осью oz (рассматриваем верхнюю сторону поверхности), нормаль к образует тупой угол с oz, т.к. строится к нижней стороне поверхности:

.

Равенство не нарушится, если к правой его части добавим интеграл по цилиндрической поверхности ₃

интеграл равен нулю, т.к. нормаль образует с осью oz угол 90, cos90 = 0 по всей поверхности ₃. Запишем символически окончательное равенство

Пример 6. Вычислить интеграл

где  – внешняя сторона замкнутой поверхности, ограниченной параболоидом х² + у² = 4  z и плоскостью xoy

Решение. Обратите внимание на то, что мы используем условие примера 3. Применим формулу Остроградского:

где Т – тело, ограниченное указанными поверхностями.

Вычислим тройной интеграл в цилиндрической системе координат:

Уравнения граничных поверхностей:

 параболоида, ограничивающего тело сверху:

 плоскости z = 0, ограничивающей тело снизу.

Интеграл записываем в виде трёхкратного в новой системе координат:

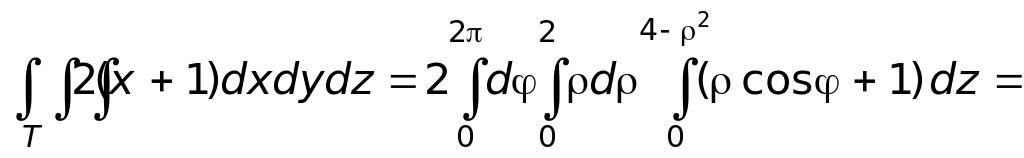
При сравнении ответов, полученных в примерах 3 и 4, убеждаемся в их идентичности и делаем вывод: задача решена верно и в том, и в другом случае.

Ошибка, которую часто допускают студенты, состоит в том, что применяют формулу Остроградского, не убедившись в выполнении условий теоремы Остроградского:

 замкнутости поверхности,

 непрерывности функций P(x, y, z), Q(x, y, z), R(x, y, z) и их частных производных на поверхности и внутри неё.

Пример 7. Вычислить интеграл где  — внешняя сторона сферы х² + у² + z² = R².

Решение

Вариант 1. Вычислим интеграл непосредственно как сумму двух слагаемых. Начнём с последнего слагаемого:

Чтобы проектирование было взаимно однозначным, сферу придётся разбить на две части:

 верхнюю полусферу – поверхность ₁, её уравнение

 нижнюю полусферу – поверхность ₂, её уравнение

при этом обе поверхности проектируются в один и тот же круг плоскости хоу

Нормаль к верхней полусфере ₁ образует острый угол с осью oz, cos  0.

Нормаль к нижней полусфере ₂ образует тупой угол с осью oz, cos  0.

Итак,

Перейдём к вычислению первого слагаемого составного интеграла

Чтобы перевести его в двойной интеграл, проектируем сферу на координатную плоскость yoz, получая при этом сумму двух поверхностных интегралов по двум половинкам сферы (ближней ₃ и дальней ₄):

Устанавливаем уравнение каждой из этих поверхностей и угол между нормалью и осью ох (см. рис. 19)

нормаль образует острый угол с положительным направлением оси ох, cos  0 (стрелка нормали обращена к нам, как и сама ось ох)

Обе половинки сферы проектируются в круг радиуса R плоскости yoz. Обозначим эту область D_yz (см. рис..20).

Теперь можно вычислить поверхностный интеграл

Перейдём в полярную систему координат

Итак,

Вариант 2. Вычислим интеграл I с помощью формулы Остроградского, учитывая, что поверхность гладкая и подынтегральные функции непрерывны и дифференцируемы в замкнутой области, ограниченной поверхностью  :

Полученный тройной интеграл вычислим в сферических координатах ,

последнее слагаемое равно нулю, поэтому окончательно получим