2.2. Понятие двухсторонней поверхности. Ориентация поверхности

Рассмотрим поверхность  (незамкнутую) (см. рис. 8). Построим к ней нормаль в произвольно выбранной точке M(x,y,z). Очевидно, можно говорить о двух сторонах поверхности так же, как о двух направлениях нормали.

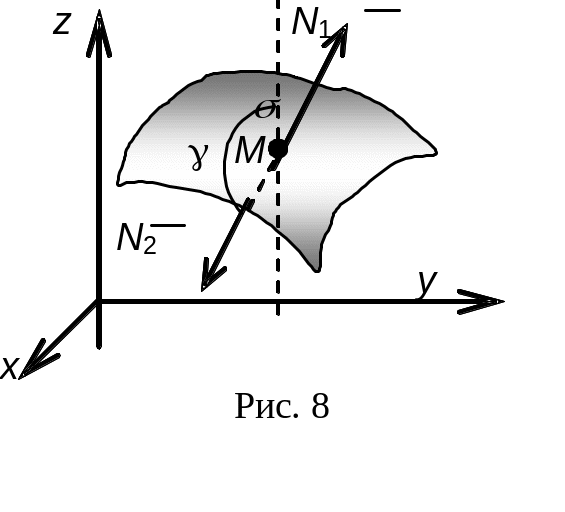
Например, с осью z нормаль образует острый угол, и эту сторону поверхности обычно называют верхней. Нормаль образует с осью oz тупой угол , сторону поверхности, к которой построена нормаль , назовём нижней. Если поверхность замкнута, то можно говорить о её внешней и внутренней сторонах.

С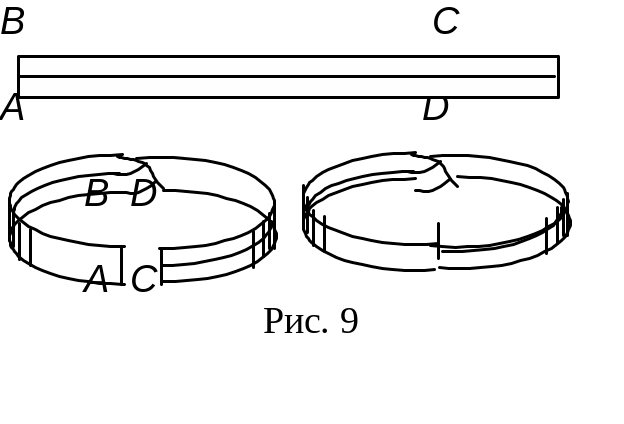 уществуют и односторонние поверхности, классическим примером которых служит так называемый лист Мёбиуса (рис. 9), если, выбрав точку М, построить в ней нормаль и двигать эту нормаль непрерывно вдоль какой-то кривой на поверхности, мы вернёмся в точку М с тем же направлением нормали. Или, начав красить с какого-то места, вы закрасите всю поверхность, вернувшись в то же место, не переходя границы поверхности.

Модель листа Мёбиуса можно получить, если прямоугольную полоску бумаги, перекрутив один раз, склеить так, чтобы точка А совпала с точкой С, а точка В совпала с точкой D.

Мы будем иметь дело только с двухсторонними (ориентированными) поверхностями.

Введём понятие ориентированной поверхности.

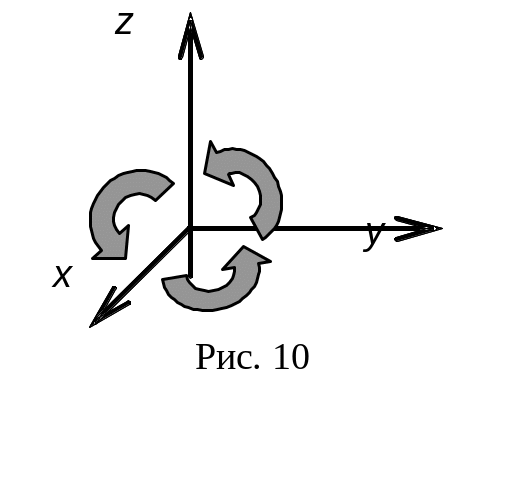
Вспомните определение векторного произведения. Векторное произведение вектора на вектор — это третий вектор , направленный перпендикулярно плоскости перемножаемых векторов так, что с его конца поворот от вектора к вектору видится против часовой стрелки. Такое расположение трёх векторов соответствует расположению осей правой системы координат (см. рис. 10)

Пусть  — незамкнутая гладкая двухсторонняя поверхность, ограниченная гладким контуром L. Припишем контуру L определённое направление обхода. Будем считать контур L положительно ориентированным, если при взгляде с конца вектора (см. рис. 11) обход контура происходит против часовой стрелки, т. е. сама поверхность остаётся слева от кривой L. При этом условии выбранной стороне поверхности приписывается нормаль, направляющие косинусы которой берутся со знаком плюс, и поверхность называют положительно ориентированной.

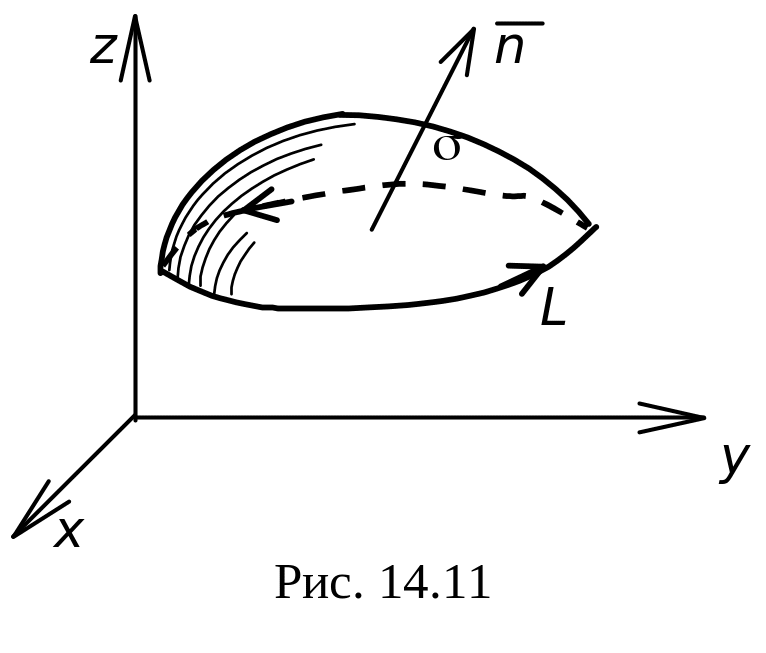
Если рассмотреть другую сторону поверхности, то нормали в выбранных точках изменят своё направление на противоположное, изменится и направление обхода контура L, поверхность изменит свою ориентацию. Таким образом, если придерживаться

установленного правила, выбор стороны поверхности и определяет её ориентацию.

Теперь вычислим массу полусферы

Выбор положительного направления обхода контура (границы) поверхности однозначно определяет её сторону. На рис. 11 нормаль образует острый угол с осью oz (cos > 0), что соответствует обходу контура L в положительном направлении, т. е. против часовой стрелки.

2.3. Поверхностный интеграл второго типа (по проекциям)

Пусть в каждой точке двухсторонней поверхности  задана непрерывная функция f(x, y, z). Выберем на поверхности определённую сторону, разобьём её сетью произвольных кривых на п участков , на каждом из которых произвольно выберем точку

, где .

Вычислим значения функции f_i = f(M_i), где i = 1, 2, …, n.

На каждом из участков _i в выбранной точке M_i построим к выбранной стороне поверхности нормаль .

Спроектируем каждый из участков _i на плоскость xoy, обозначив S_i площадь проекции i–го участка. Составим произведения f_iS_i, причём, если нормаль образует острый угол с осью oz, берём произведение со знаком плюс, если нормаль образует тупой угол с осью oz, берём произведение со знаком минус. Суммируем все произведения:

.

Обратите внимание: слагаемые суммы в отличие от предыдущих интегральных сумм, распространяют на весь участок _i не только значение функции f(M_i), но и направление нормали, построенной в точке M_i.

Теорема. Если существует конечный предел интегральной суммы при стремлении к нулю диаметров всех частей _i (или maxd_i  0), не зависящий от типа разбиения и выбора точек M_i, то его называют поверхностным интегралом второго типа, распространённым на выбранную сторону поверхности, и обозначают

,

.

Аналогично определяются интегралы

, ,

причём для выбора знака проекции служит угол нормали с осью оу и ох соответственно.

Наиболее общим видом поверхностного интеграла второго типа является составной интеграл

,

где Р, Q, R — функции трёх переменных, определённые и непрерывные на поверхности .

Поверхностный интеграл обладает всеми свойствами поверхностного интеграла первого типа, за исключением одного: при изменении стороны поверхности интеграл меняет знак на противоположный.

Рассмотрим сначала третье слагаемое формулы и поставим задачу о вычислении данного интеграла.

Пусть поверхность  задана уравнением z = f(x, y) и она однозначно проектируется в область D_xy плоскости xoy. Тогда

,где знак (+) берётся, если на выбранной стороне поверхности , и знак () берётся, если cos < 0.

Аналогично рассуждая, получим формулы для вычисления оставшихся слагаемых составного интеграла.

Пусть поверхность  задана уравнением y = (x, z) и она однозначно проектируется на плоскость xoz в область D_xz. Тогда

Знак (+) берём, если на выбранной стороне поверхности , и знак () берём, если cos < 0.

Первое слагаемое формулы (14.7) вычисляется с помощью двойного интеграла

,

где x = (y,z) — уравнение поверхности ;

D_yz — проекция поверхности  на плоскость yoz.

Знак (+) берём, если , знак () берём, если cos < 0 на выбранной стороне поверхности .

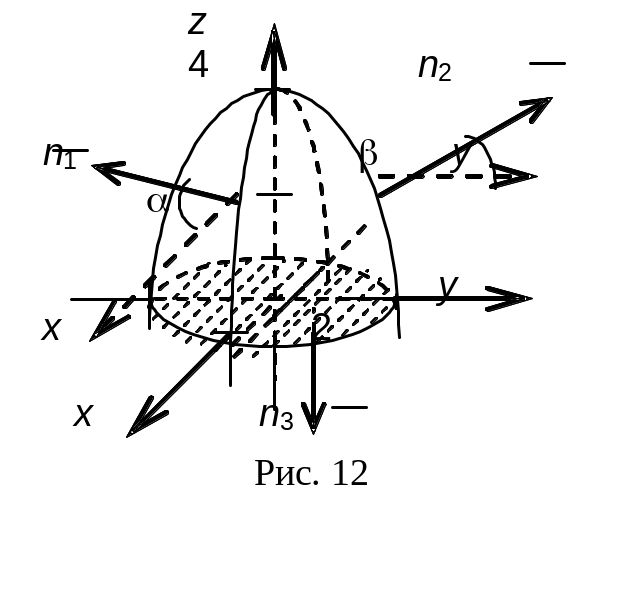
Пример 4. Вычислить

где  — внешняя сторона замкнутой поверхности

Решение. Вычислим первое слагаемое составного интеграла

где ₁ — ближняя к нам половина параболоида (см. рис. 12), её уравнение: , нормаль образует острый угол с осью х, cos > 0,

₂ – дальняя часть параболоида, её уравнение: cos < 0,

Вычислим второе слагаемое составного интеграла:

где ₃ — правая половинка параболоида (см. рис. 14.12), её уравнение: , нормаль образует острый угол с осью у, cos > 0,

₄ — левая половина параболоида, её уравнение: cos < 0,

где область D_xz ограничена линиями x² = 4 – z, z = 0

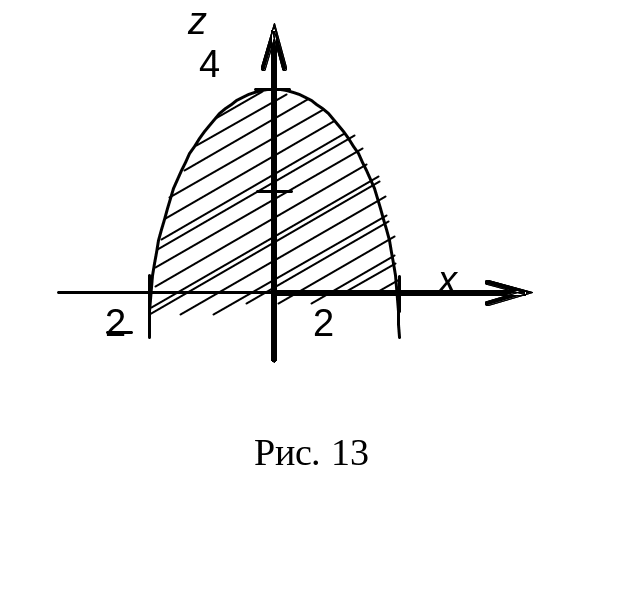
Вычисляем двойной интеграл

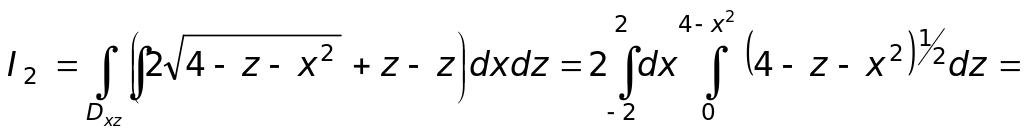
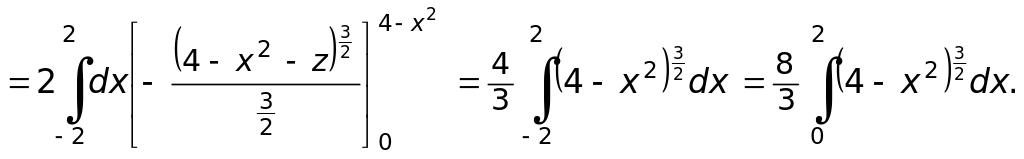
Чтобы избавиться от иррациональности, выполняем подстановку:

Пределы интегрирования:

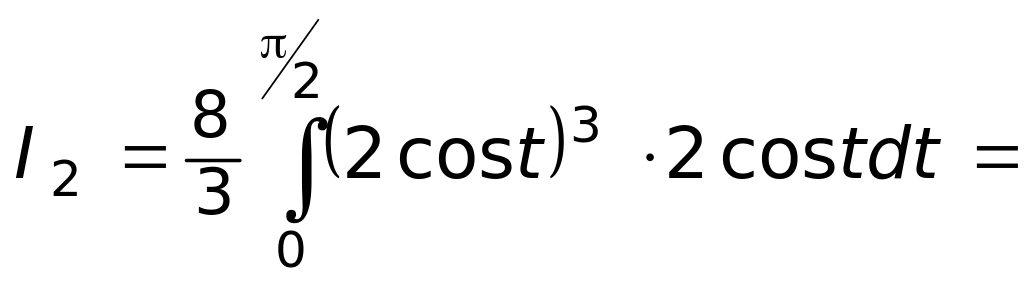
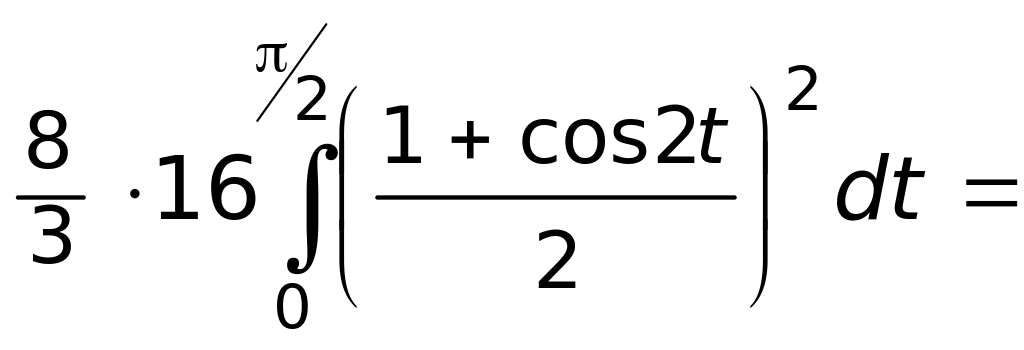
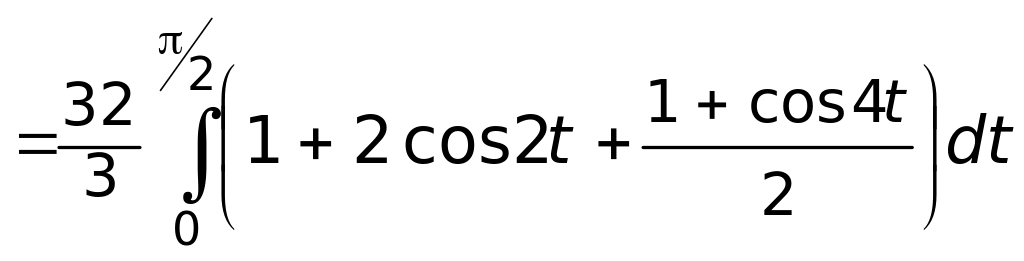
Вычисляем последнее слагаемое составного интеграла

где ₅ — внешняя сторона параболоида нормаль к которой образует с осью z острый угол, cos > 0,

₆ — это плоскость z = 0, внешняя нормаль образует с осью z угол  = 180, cos < 0 (см. рис. 12).

Обе поверхности ₅, ₆ проектируются в один и тот же круг х² + у²  4 плоскости хоу (см. рис12).

Переводим поверхностный интеграл в двойной:

Для вычисления последнего интеграла используем полярную систему координат (x = cos, y = sin, I = , уравнение окружности х² + у² = 4 преобразуется к виду  = 2), тогда

Итак,