2. Поверхностные интегралы

2.1. Поверхностные интегралы первого типа

К понятию интеграла по поверхности приводит, например, задача о вычислении массы, распределённой по поверхности  с переменной поверхностной плотностью f(M).

Решим эту задачу.

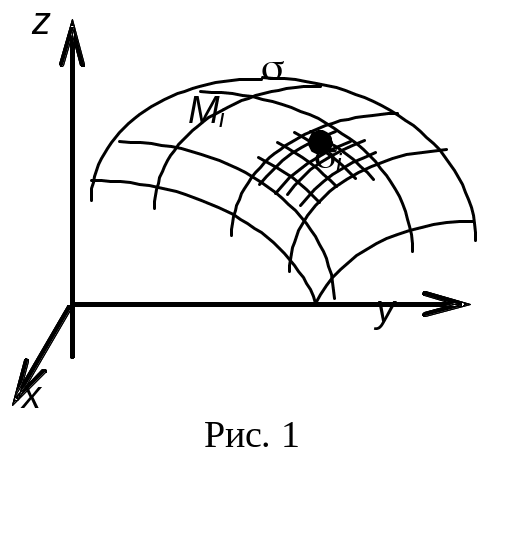
Разобьём поверхность  произвольным образом на п частей _i (см. рис. .1) и выберем в каждой из них (также произвольно) точку M_i. Если части _i достаточно малы, то за их массу можно принять произведение , , где – площадь i-го участка поверхности (т.е. мы предполагаем, что каждый из участков _i однородный с плотностью f(M_i), где i = 1, 2, …, n), тогда масса всей поверхности

Это значение тем точнее, чем меньше участки _i. Переходя к пределу при n  , а значит, уменьшая размер каждого участка, получим точное значение массы поверхности

К аналогичным пределам приводят и другие задачи физики, эти пределы называются поверхностными интегралами первого типа.

Теорема. Если при стремлении диаметров всех частей _i к нулю интегральная сумма (1) имеет конечный предел, не зависящий ни от способа разбиения поверхности  на части, ни от выбора точек M_i, то этот предел называется поверхностным интегралом первого рода и обозначается

Заметим, что этот интеграл обладает всеми свойствами криволинейного интеграла первого типа и, в частности, если подынтегральная функция f(x, y, z) = 1, получаем формулу для вычисления площади поверхности 

.

Интегралу (2) можно придать механический смысл: если f(x, y, z) =  — переменная плотность материальной поверхности , то масса этой неоднородной поверхности

.

Выведем формулу для вычисления интеграла (2).

Пусть поверхность  однозначно проектируется в область D плоскости хоу. Тогда

,

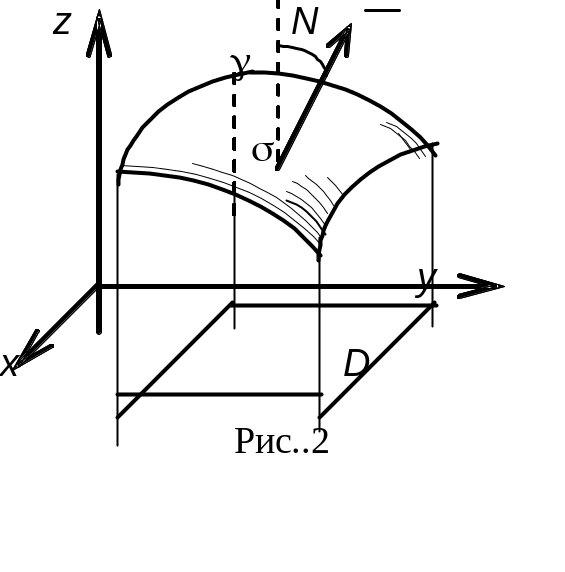
где  — угол между нормалью к поверхности  и осью (см. рис. 2).

Если поверхность  описывается уравнением z = z(x, y), то

Подставив этот дифференциал в (2), получим формулу для вычисления поверхностного интеграла по поверхности 

где D_xy – проекция поверхности на плоскость хоу.

Таким образом, чтобы вычислить поверхностный интеграл первого типа, необходимо перевести его в двойной интеграл по области D, полученной в результате проектирования поверхности  на одну из координатных плоскостей (проектирование должно быть взаимно однозначным: одна точка поверхности проектируется в одну точку плоскости), подсчитать элемент d и выразить подынтегральную функцию через выбранные переменные.

Пример 1. Вычислить , где  — конечная часть параболоида , отсечённая плоскостью х = 0.

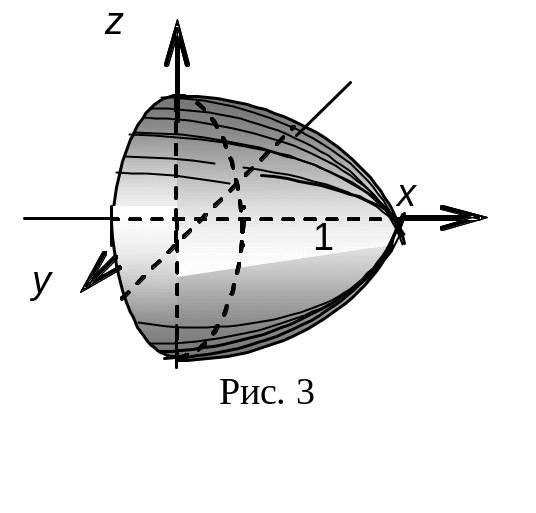
Решение. Построим поверхность (см. рис. 3) и выберем координатную плоскость для проектирования. Очевидно, — это плоскость yoz, т. к. все точки параболоида однозначно проектируются в точки круга плоскости (на другие координатные плоскости будет проектироваться по две половины параболоида).

Подсчитаем элемент d поверхности , предварительно найдём частные производные

, ;

.

Переводим поверхностный интеграл в двойной по области D_yz (см. рис. 14.4), заменяя в подынтегральной функции “лишнюю” переменную х из уравнения поверхности

.

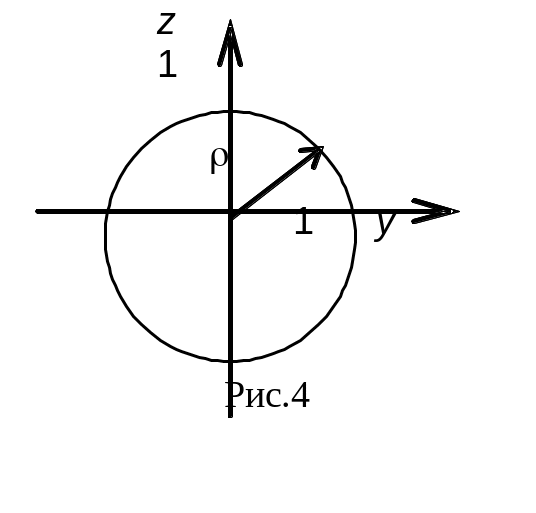
Вычисляем двойной интеграл в полярной системе координат, подставляя формулы перехода в подынтегральное выражение:

, , якобиан ,

Пример 2. Вычислить массу цилиндрической поверхности , отсечённой плоскостями х = 0, х = 4, если плотность в каждой её точке есть функция .

Решение. Построим поверхность (см. рис.5) и выберем координатную плоскость для проектирования. Из рисунка видно, что при проектировании поверхности на плоскость zoy получаем незамкнутую линию – полуокружность; на плоскость zox проектируются одновременно две части цилиндра, условие однозначности нарушается; и только на плоскости xoy получаем замкнутую область (см. рис. 6), причём одна точка цилиндра проектируется в одну точку прямоугольника.

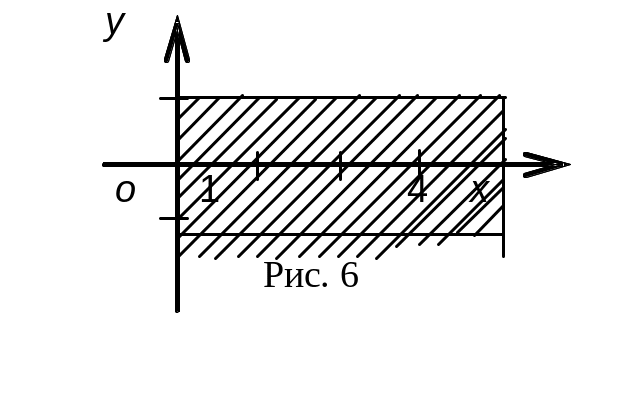
Подсчитаем дифференциал ;

Составим поверхностный интеграл и переведём его по формуле (14.5) в двойной интеграл по переменным х, у. Заменим лишнюю переменную z в подынтегральной функции, используя уравнение цилиндра

Ответ: m = 16.

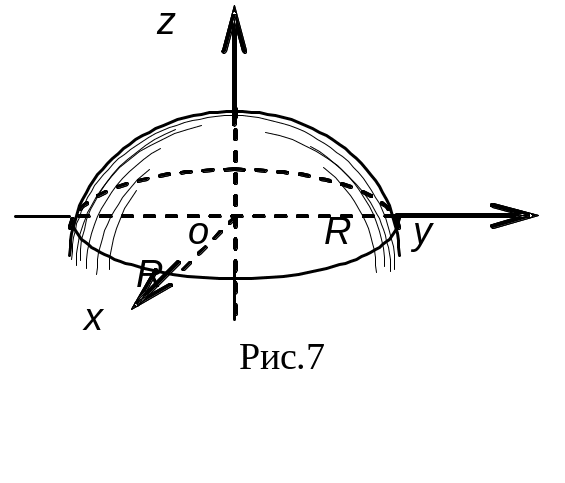
Пример 3. Найти центр масс однородной полусферы радиуса R.

Решение. Выберем систему координат так, чтобы начало координат совпало с центром сферы и плоскость хоу была основанием полусферы (см. рис. 7), тогда уравнение сферы примет вид

и соответственно уравнение полусферы

Координаты центра тяжести (центра масс) найдём по формулам

Поскольку полусфера симметрична оси z, её центр масс находится на оси oz, т. е.

где М_ху – статический момент поверхности относительно плоскости хоу,

т_ – масса полусферы.

Вычислим статический момент

где  – плотность поверхности (по условию  = const),

(здесь D_xy – круг радиуса R в плоскости хоу и двойной интеграл выражает его площадь S = R²).

т. к.  = const, а площадь полусферы известна (площадь сферы 4R²).

Окончательно

Ответ: