Модуль 9. Дифференциальные уравнения

1. Дифференциальные уравнения I порядка. Уравнения с разделяющимися переменными

1.1. Дифференциальные уравнения I порядка. Общие понятия

Обыкновенным дифференциальным уравнением 1 порядка называется уравнение вида

, (1.1)

связывающее независимую переменную x, искомую функцию и её производную .

При изложении теории дифференциальных уравнений чаще всего рассматриваются уравнения, разрешенные относительно производной :

(1.2)

или уравнения в так называемой симметричной форме:

. (1.3)

Пример 1.1.1. Среди данных уравнений указать обыкновенные дифференциальные уравнения I порядка.

а) ;

б) ;

в) ;

г) ;

д) ;

е) .

Ответ: б); в); д); е).

Частным решением дифференциального уравнения называется любая функция , которая, будучи подставленной вместе со своей производной в уравнение, обращает его в тождество

Любое дифференциальное уравнение имеет бесчисленное множество решений.

Множество всех частных решений дифференциального уравнения называется его общим решением.

Общее решение дифференциального уравнения I порядка является функцией, зависящей от одной произвольной постоянной

Если решение найдено в неявной форме

то его называют общим интегралом дифференциального уравнения.

Пример 1.1.2. Дано уравнение и функции

а) ; б) ;

в) ; г) .

Какая из функций является частным решением уравнения? Какая из функций является общим решением уравнения?

Ответ: а); в).

Задача Коши для уравнений I порядка: найти решение, которое удовлетворяло бы начальным условиям

где - заданные числа.

Теорема существования и единственности решения задачи Коши. Если функция уравнения (1.2) непрерывна в области D и имеет в ней непрерывную частную производную , то для любой внутренней точки области D задача Коши имеет единственное решение, удовлетворяющее условиям .

С геометрической точки зрения:

общее решение в декартовой системе координат при различных значениях произвольной постоянной изображает множество кривых, которые называют интегральными кривыми;

задача Коши состоит в отыскании той интегральной кривой, которая проходит через заданную точку ;

дифференциальное уравнение в каждой точке области D определяет угловой коэффициент касательной к интегральной кривой, проходящей через эту точку, т.е. задает на плоскости поле направлений.

С механической точки зрения:

дифференциальное уравнение - математическая модель изменения скорости движения некоторого физического тела;

общее решение определяет общие законы движения тела;

начальные условия содержат информацию о начальном состоянии тела в определенный момент времени;

частное решение определяет такой закон движения, из которого можно получить конкретные качественные результаты о состоянии тела в любой момент времени.

В таблице 1 помещены типы дифференциальных уравнений I порядка, которые будут изучаться на занятиях.

1.2. Дифференциальные уравнения с разделяющимися переменными

Дифференциальное уравнение I порядка называется уравнением с разделяющимися переменными, если его правая часть есть произведение функций, одна из которых зависит от переменной x , другая – от y: .

Уравнение, записанное в симметричной форме является уравнением с разделяющимися переменными, если множители и представляют собой произведение функций, из которых одна зависит только от переменной x , другая – от переменной y : .

Пример 1.2.1. Среди данных уравнений указать уравнения с разделяющимися переменными:

а)

б)

в)

г)

д) .

Ответ: а); б); в); д).

Разделить переменные – значит преобразовать уравнение так, чтобы каждая переменная содержалась только в том слагаемом, которое содержит её дифференциал.

Для этого достаточно уравнение привести к форме

и умножить обе его части на функцию , в результате чего получится

.

Таблица 1

Типы дифференциальных уравнений I порядка

Тип уравнения	Стандартная форма записи	Особенности	Метод решения
С разделяющимися переменными		При дифференциалах – произведения функций, зависящих одна от x, другая – от y
		Правая часть – произведение функций, зависящих одна от x, другая – от y
Однородное		Правая часть – однородная функция нулевого порядка
		- однородные функции одинакового порядка
В полных дифференциалах
Линейное		Первой степени относительно и
		Первой степени относительно и
Бернулли		Отличается от линейного правой частью	Аналогично линейным

Полученное равенство можно проинтегрировать:

Уравнение необходимо разделить почленно на выражение . Получаем равенство

,

которое можно проинтегрировать:

.

Пример 1.2.2. Найти решение задачи Коши для уравнения , удовлетворяющее начальным условиям .

1⁰. Определим тип уравнения (таблица 1):

- уравнение с разделяющимися переменными, так как его правая часть зависит только от переменной y.

2⁰. Разделим переменные:

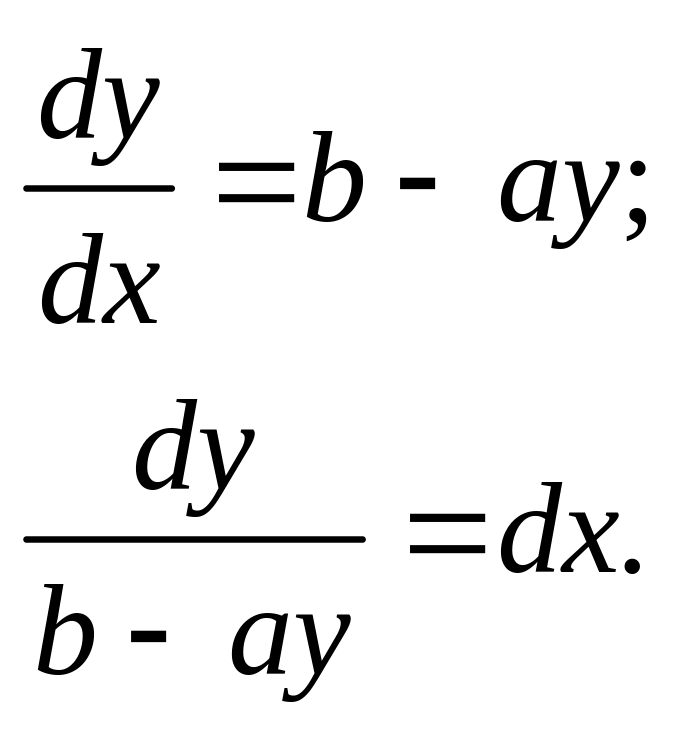
3⁰. Проинтегрируем полученное равенство:

.

4⁰. Упростим результат интегрирования и запишем общее решение (общий интеграл) уравнения:

,

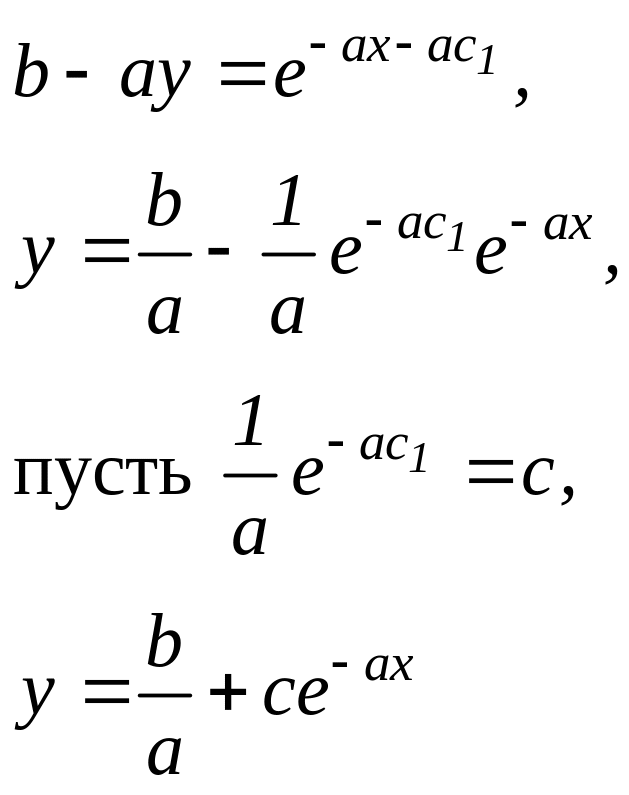
5⁰. Найдём значение произвольной постоянной: подставляя начальные условия x=0, y=0 в общее решение, находим .

6⁰. Запишем ответ – частное решение уравнения:

Пример 1.2.3. Найти решение задачи Коши для уравнения , удовлетворяющее начальным условиям y(0)=1.

1⁰. Определим тип уравнения:

- уравнение с разделяющимися переменными,

где , .

2⁰. Разделим переменные:

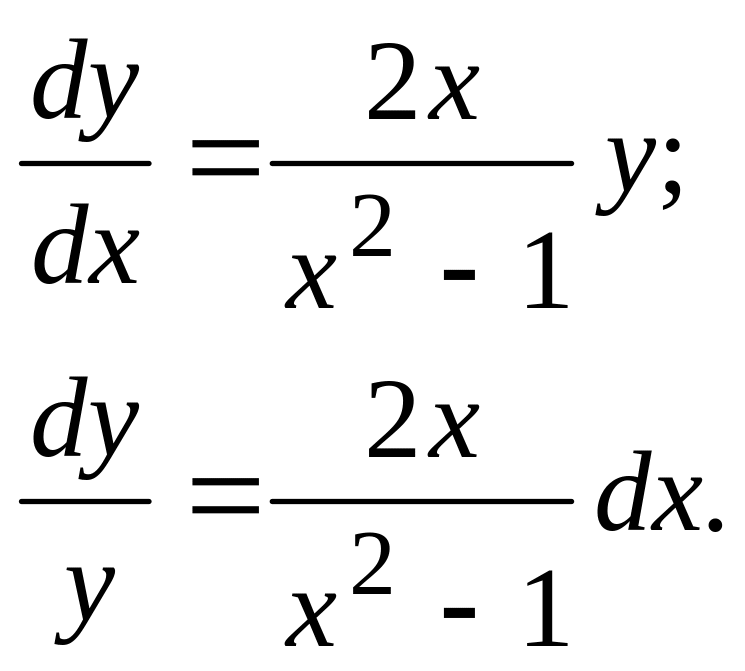
3⁰. Проинтегрируем обе части равенства:

.

Для удобства преобразований постоянная выбрана в логарифмической форме.

4⁰. Упростим результат интегрирования:

5⁰. Подставим начальные условия. При x=0, y=1 получаем с= .

6⁰. Запишем ответ: .

Пример 1.2.4. Среди интегральных кривых, удовлетворяющих уравнению

найти ту, которая проходит через точку

Ответ: .

Пример 1.2.5. Найти общее решение дифференциального уравнения

Указание: применить формулу

Ответ: .