1.5. Связь между криволинейными интегралами первого и второго типов

Для начала вспомним геометрический смысл производной

Это выражение — угловой коэффициент касательной к графику функции у = f(х) в точке М(х, у). Пусть дуга АВ линии L задана функцией у = f(х) и в точке М к ней проведены касательная МТ и секущая ММ₁ (см. рис. 13). Тогда

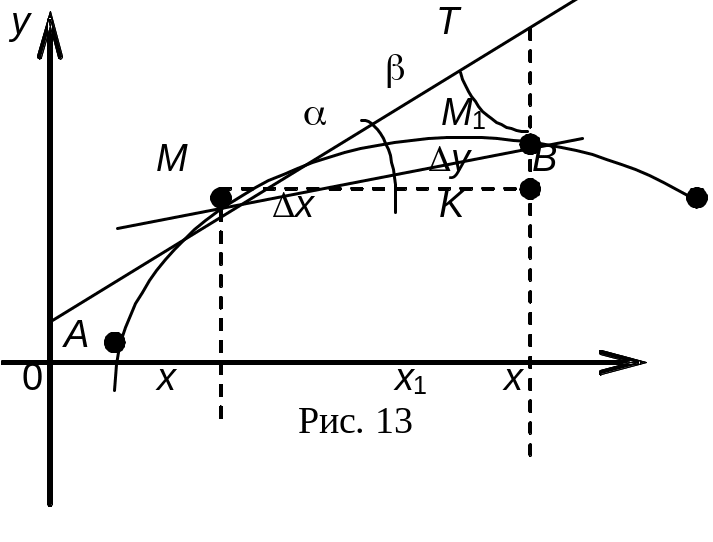
где у = у₁  у, х = х₁  х,

 — угол между касательной и осью ох.

Запишем уравнение линии в параметрическом виде

Производная функции, заданной параметрически, вычисляется по формуле

и формально имеем

Покажем, что это действительно так.

Возьмём в качестве параметра дугу l так, что точкe M(x, y) соответствует дуга , а точке М₁ соответствует дуга , координаты точки М₁: х + х = х₁, у + у = у₁.

Вектор имеет длину

Длина дуги равна .

Рассмотрим предел отношения длины хорды ММ₁ к длине дуги, когда точка М₁ стремится к точке М:

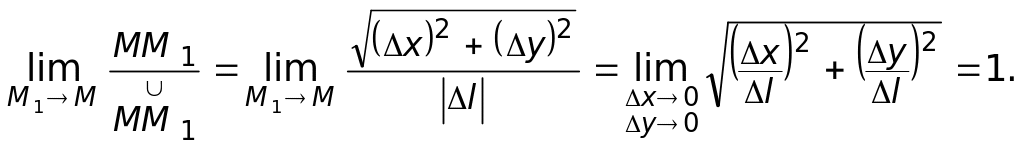
Это значит, что мы имеем дело с эквивалентными бесконечно малыми, т.е. во всех рассуждениях можем длину дуги заменить длиной хорды (или длиной вектора ). В результате получаем дифференциал дуги (по любому параметру)

Теперь можно записать связь между двумя типами криволинейных интегралов:

где L — дуга АВ и sin = sin(90  ) = cos, где   угол между касательной и осью оу. Тогда

.

Подчеркнём, что угол  связан с тем направлением касательной, которое отвечает выбранному направлению дуги АВ. Если изменить направление, криволинейный интеграл слева, а значит, и справа изменит знак на противоположный.

Для трёхмерного пространства запишем аналогичную формулу

где cos, cos, cos — направляющие косинусы касательной в предположении, что её направление совпадает с направлением интегрирования.

1.6. Приложения криволинейного интеграла первого рода к решению некоторых задач механики

 Если  = (х, у) — линейная плотность плоской материальной кривой АВ, то численное значение массы кривой АВ равно интегралу

В случае пространственной кривой АВ соответственно

 Координаты центра тяжести (х₀, у₀) плоской кривой вычисляются по формулам

для пространственной кривой АВ

 Статические моменты материальной кривой относительно оси ох и оси оу соответственно определяются интегралами

 Моменты инерции относительно координатных осей вычисляются по формулам

где r_x, r_y, r_z — расстояния от точки до соответствующих осей координат.

Пример 12. Вычислить массу отрезка прямой, заключённого между точками А(0, 2) и В(4, 0), если плотность

Решение. Запишем уравнение пути интегрирования как прямой, проходящей через две точки:

Отсюда

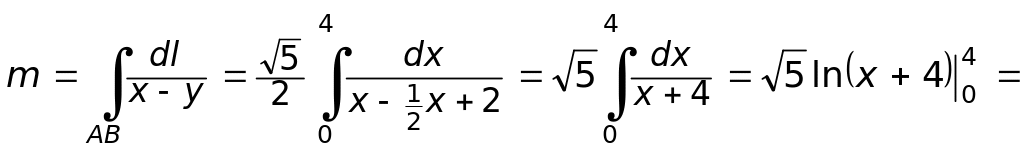
Пример 13. Найти статические моменты дуги однородной астроиды относительно осей координат.

Решение. Дуга астроиды однородна, следовательно, плотность в каждой точке постоянна. Пусть  = ₀. Запишем уравнение астроиды в параметрическом виде

где х  0, у  0, ;

По условию следовательно,

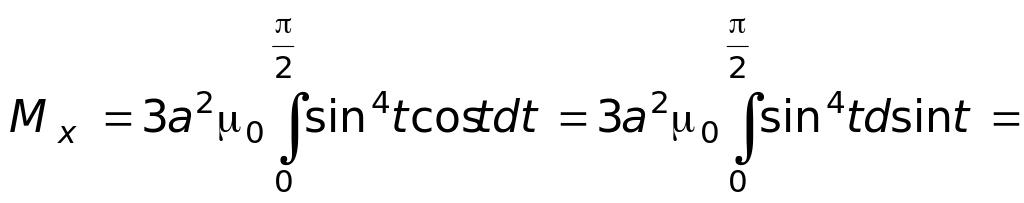
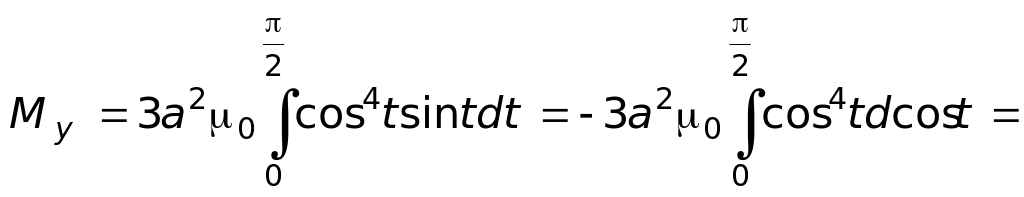
Пример 14. Найти моменты инерции относительно координатных осей одного витка однородной винтовой линии

x = acost, y = asint, (0  t  2).

Решение. Плотность кривой примем равной  = ₀ . Расстояния от произвольной точки M(x, y, z) до осей координат

Отсюда

аналогично

Замечание. При вычислении интегралов I_x, I_y мы воспользовались следующими преобразованиями: