1.4. Условия независимости криволинейного интеграла от пути интегрирования

Как мы видели, вычисление криволинейного интеграла

непосредственно зависит от самой линии L, отсюда и величина его зависит от вида кривой.

Поставим задачу: выяснить условия, при которых бы криволинейный интеграл не зависел от пути интегрирования, а только от его начальной и конечной точек. Так, с точки зрения механики независимость линейного интеграла от линии интегрирования будет обозначать, что величина работы в силовом поле

не зависит от формы пути, а только от его начальной и конечной точек.

Лемма. Для того, чтобы криволинейный интеграл

в некоторой области D плоскости хоу не зависел от пути интегрирования, необходимо и достаточно, чтобы интеграл по любому замкнутому контуру, лежащему в этой области, был равен нулю.

Доказательство

 Достаточность. Пусть интеграл

,

где L — любой замкнутый контур, принадлежащий области D.

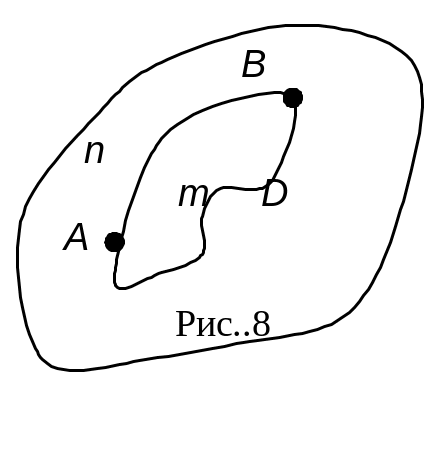
Покажем, что этот интеграл не зависит от пути интегрирования. Действительно, пусть А и В – две точки области D. Соединим их двумя различными, произвольно выбранными кривыми АтВ и АпВ, лежащими в области D (рис. 13.8). Покажем, что

.

Дуги АтВ и АпВ образуют замкнутый контур . По свойствам (3 и 1) криволинейных интегралов

.

Следовательно,

, или ,

т. е. криволинейный интеграл не зависит о пути интегрирования.

 Необходимость. Пусть в области D криволинейный интеграл

не зависит от пути интегрирования. Покажем, что интеграл по любому замкнутому контуру, лежащему в этой области, равен нулю.

Действительно, рассмотрим произвольный замкнутый контур, лежащий в области D, и возьмём на нём две произвольные точки А и В (рис 7.). Тогда

,

т.к. по условию

.

Итак, интеграл по любому замкнутому контуру L, лежащему в области D, равен нулю. Лемма доказана.

Докажем теперь основную теорему.

Теорема 3. Пусть функции Р(х, у) и Q(x, y) непрерывны вместе со своими частными производными первого порядка в области D, ограниченной одним замкнутым контуром. Тогда для того, чтобы криволинейный интеграл

не зависел от линии интегрирования, необходимо и достаточно, чтобы во всех точках области D выполнялось равенство

Теорема 4 (о нахождении функции по полному дифференциалу). Если функции P(x, y), Q(x, y) определены и непрерывны в области D плоскости хоу и имеют в ней непрерывные частные производные , то выражение Pdx + Qdy является полным

дифференциалом некоторой функции u(х, у) тогда и только тогда, когда выполняется условие

Доказательство

 Необходимость. Пусть Pdx + Qdy = du(x, y). Тогда справедливо соответствие

и .

Продифференцируем каждое из этих равенств:

По свойству смешанных производных правые части последних соотношений равны и, в силу их непрерывности (по условию теоремы), в любой точке области D выполняется равенство

Необходимость доказана.

 Достаточность. Пусть в области D выполняется тождественное равенство

Но тогда по теореме 1 линейный интеграл (15) не зависит от пути интегрирования. Установим правило нахождения первообразной функции u(х, у) по её полному дифференциалу, тем самым доказав её существование.

Выберем в области D какую-то фиксированную точку А(х₀, у₀) и переменную точку М(х, у). Линейный интеграл (13.15) будет функцией верхнего предела

 Пусть точка М переместилась (см. рис. 13.10) в положение М₁(х + х, у). Тогда функция Ф(х, у) получит частное приращение по переменной х

П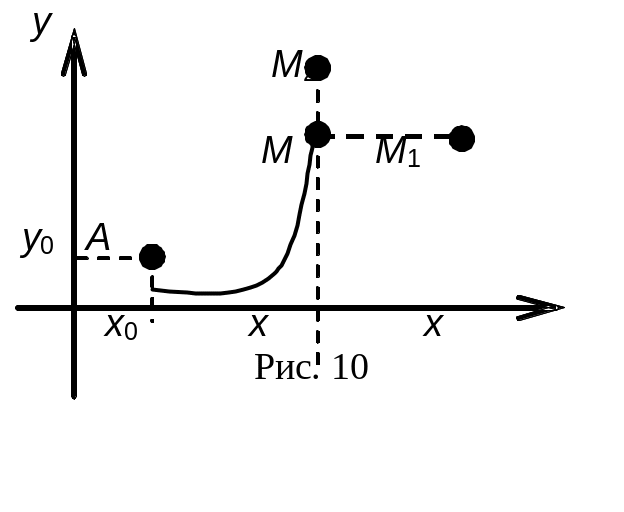 оскольку переменная у не получила приращения на отрезке ММ₁ (у = 0, у = const), то подынтегральное выражение в последнем интеграле зависит от одной переменной х, а интеграл является определённым.

Применим к нему теорему о среднем:

где .

Разделив на х, получаем

или, переходя к пределу при х  0, в силу непрерывности функции Р(х, у), имеем

 Пусть теперь точка М движется параллельно оси оу, т. е. функция Ф(х, у) получает приращение по переменной у, при этом х = 0:

где М₂(х, у + у).

Проводя рассуждения, аналогичные предыдущим, приходим к заключению, что

Сложив результаты, получаем формулу полного дифференциала некоторой функции Ф(х, у)

Интегрируя, находим одну из первообразных линейного интеграла

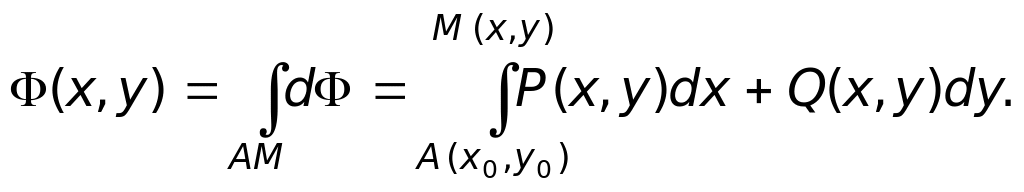
Сформулируем правило отыскания функции. Поскольку подынтегральное выражение — полный дифференциал некоторой функции, линейный интеграл не зависит от пути интегрирования. Выберем самый удобный путь, соединяющий точки А(х₀, у₀) и М(х, у), например, ломаную АВМ с отрезками, параллельными осям (см. рис. 11). Исследуем эти отрезки:

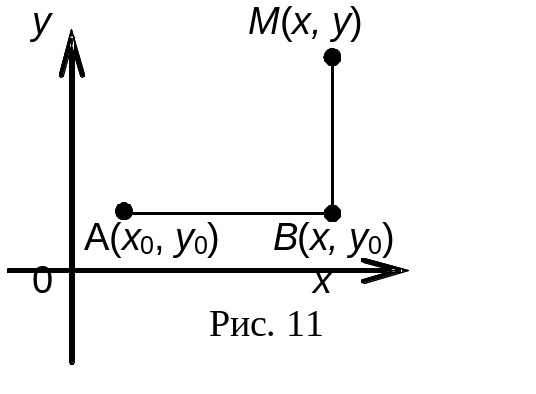
Переходим к вычислению интеграла

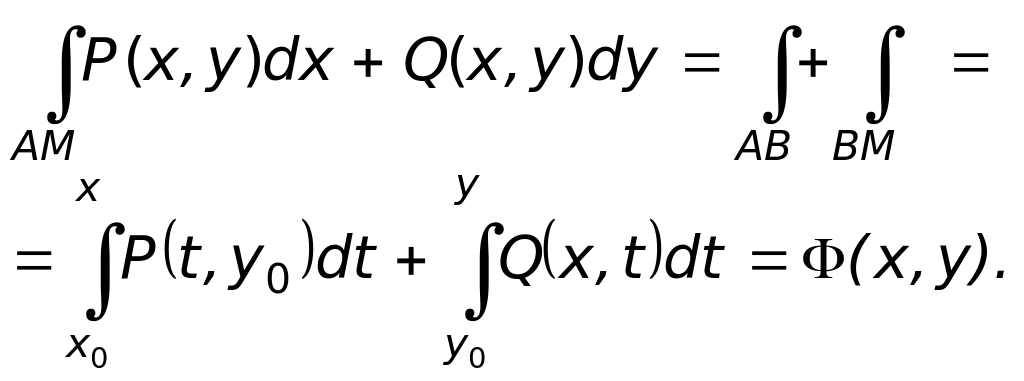
Теорема доказана. Мы получили метод отыскания функции по её полному дифференциалу, доказав таким образом факт существования такой функции.

Последнюю формулу чаще записывают в виде

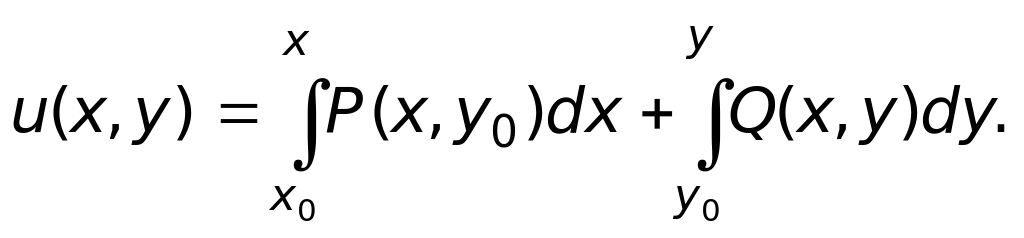
Получим ещё один результат, проанализировав формулу каждое слагаемое которой является определённым интегралом с переменным верхним пределом, подынтегральное выражение каждого из них зависит от переменной t. Применим к ним формулу Ньютона-Лейбница, учитывая, что подынтегральное выражение криволинейного интеграла в левой части равенства есть полный дифференциал некоторой функции, т. е.

Откуда следует, что

Тогда

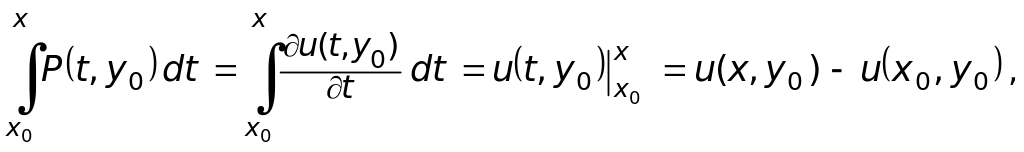
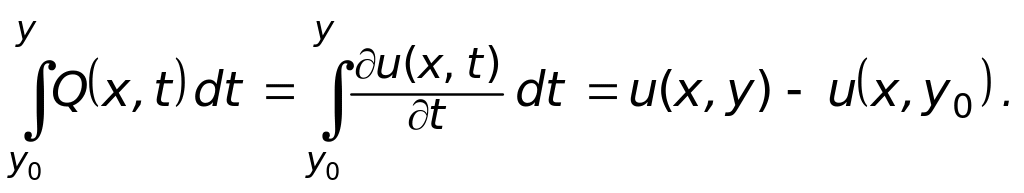
Следовательно,

или

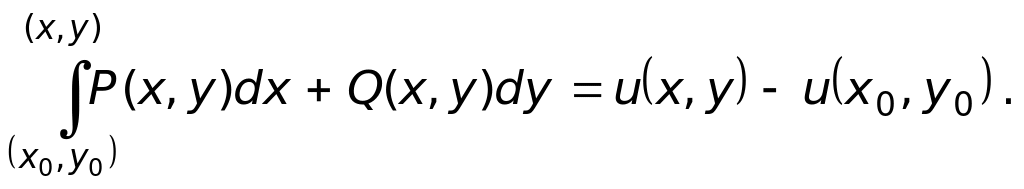
Последнее равенство является формулой Ньютона-Лейбница для криволинейного интеграла, подтверждающей вывод: интеграл от полного дифференциала не зависит от пути интегрирования, а зависит только от начальной и конечной точек интегрирования.

Пример 10. Вычислить 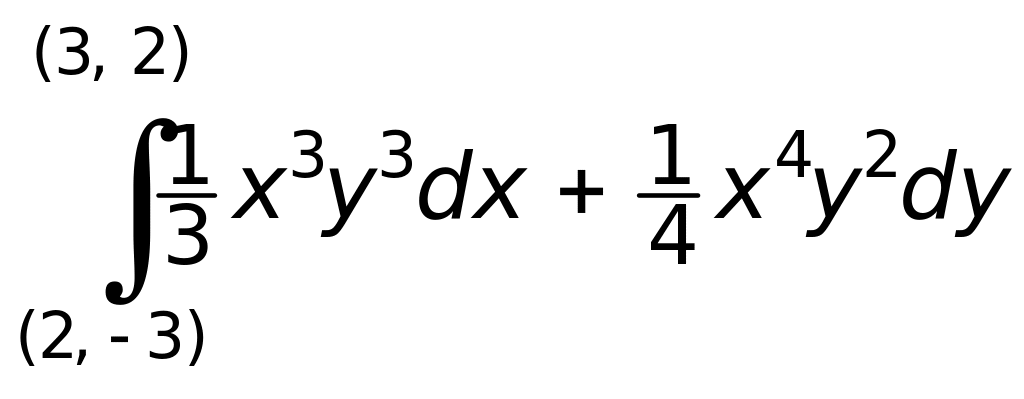вдоль любого пути.

Решение. Проверим, является ли подынтегральное выражение полным дифференциалом. Введём обозначение и сравним частные производные:

Частные производные равны, значит, интеграл не зависит от пути интегрирования.

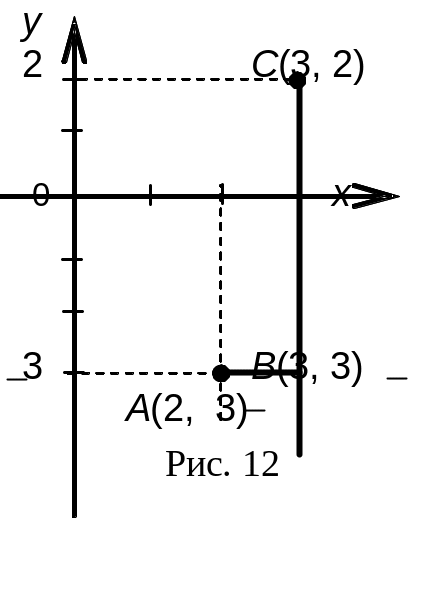
Выберем путь интегрирования, соединив точки А(2, 3) и С(3, 2) ломаной АВС (см. рис. 13.12), где В(3, 3) – промежуточная точка. Тогда

Найдём уравнения участков ломаной и соответствующие дифференциалы:

Вычислим интеграл

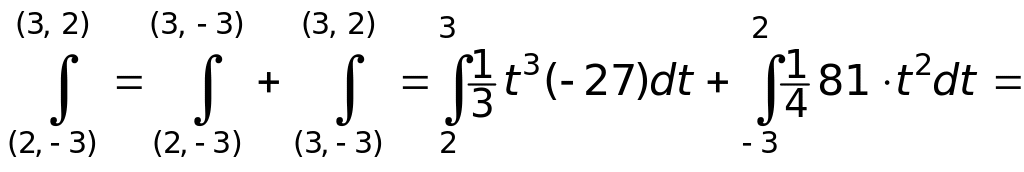
Пример 11. Найти функцию по её полному дифференциалу

Решение. В том, что данное выражение есть полный дифференциал, мы убедились при решении предыдущего примера, поэтому сразу перейдём к отысканию функции по формуле (22):

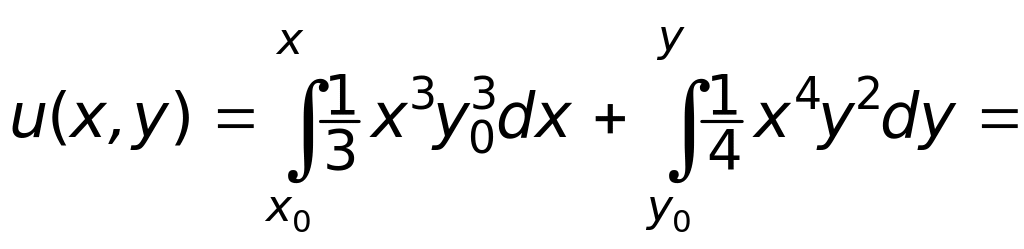
Мы получили искомую функцию с точностью до константы. Обозначив запишем ответ:

Проверим с помощью найденной функции ответ предыдущего примера, вычислив разность u(x, y)  u(x₀, y₀) = u(C)  u(A):

Ответы совпали.