1.3. Формула Грина

Установим связь криволинейного интеграла по замкнутому контуру L (гладкому или кусочно-гладкому) с двойным интегралом по плоской области D, ограниченной этим контуром.

Теорема 2 (Грина). Если:

1) — односвязная область плоскости хоу, ограниченная контуром L;

2) гладкий или кусочно-гладкий контур L ориентирован против часовой стрелки, т.е. при обходе контура область остаётся слева;

3) — непрерывные функции в вместе со своими частными производными первого порядка,

то имеет место формула Грина

.

Доказательство. Пусть — односвязная область, т.е. прямые, параллельные каждой из осей оу, ох, пересекают область не более чем в двух точках (см. определение правильной области, гл. 12). Заключив область в описанный прямоугольник (см. рис.6), получим две пары крайних точек области:

 точки А и В, которые разобьют контур на две линии: дугу с уравнением и дугу с уравнением , при этом область проектируем на ось ох, получаем отрезок ;

 точки К и Е, делящие границу области на две линии: КАЕ с уравнением и КВЕ с уравнением , область проектируем на ось оу, получаем отрезок .

Преобразуем второе слагаемое правой части формулы (12), обозначив I₁ и проинтегрировав его по переменной у:

,

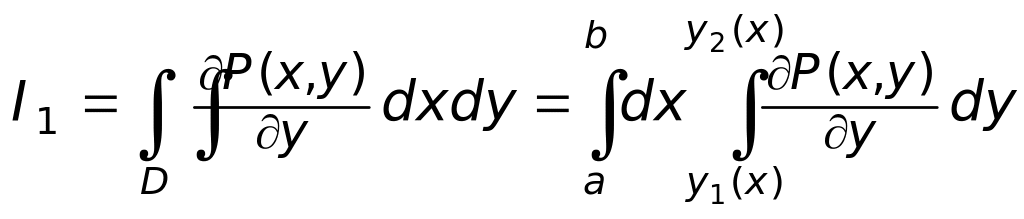т.к. функция при постоянном х есть одна из первообразных для частной производной , то имеет место равенство

.

По формуле (11) каждое из слагаемых последнего равенства представим в виде криволинейного интеграла

,

тогда

Сменив ориентацию первого слагаемого, получаем

Аналогично доказываем оставшуюся часть формулы Грина. Проектируем область D на ось оу, записываем двухкратный интеграл

Окончательно

Теорема доказана.

Вернёмся к примеру 6. Вычислим криволинейный интеграл

применив формулу Грина.

Область D в данном случае — плоскость треугольника ОАВ. Найдём частные производные функций и убедимся в их равенстве:

Отметим, что Р(х, у), Q(x, y) непрерывны и дифференцируемы в области D. Таким образом, все условия теоремы Грина выполнены. Применим теорему

Как видим, ответы совпали и данное решение оказалось намного короче предыдущего.

Замечание. Формула Грина справедлива и в случае неправильной области D. Тогда область необходимо разбить на сумму правильных областей, отвечающих условиям теоремы, например, как на рис 7. Результаты интегрирования сложить.

Таким образом, теорема Грина справедлива для любой плоской области D, ограниченной гладким или кусочно-гладким контуром.

В качестве приложения формулы Грина решим ещё одну задачу: о вычислении площади плоской области D, ограниченной замкнутой линией L. Рассмотрим функции P(x, y) = 0, Q(x, y) = x. Так как и то по формуле (12) получаем

,

или

Но по свойству двойного интеграла

где S_D — площадь области D.

Итак,

Аналогично, полагая в формуле (13.12) P = y, Q = 0, получим ещё одну формулу вычисления площади:

Сложив равенства и поделив результат на 2, получим формулу для вычисления площади области D, ограниченной линией L, с помощью линейного интеграла

Пример 9. Найти площадь фигуры, ограниченной линией

где а и b — полуоси эллипса,

– фокусное расстояние,

Решение. Воспользуемся последней формулой, перейдя к определённому интегралу по переменной t: