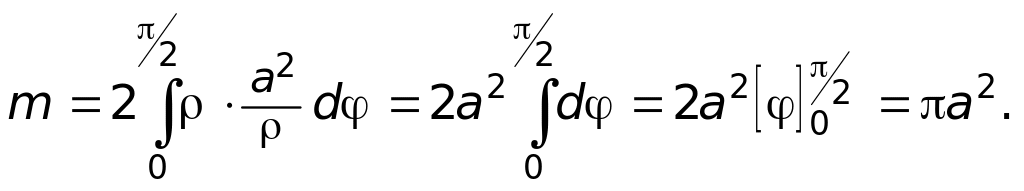2.5. Приложение тройных интегралов.

Для вычисления координат центра тяжести тела нужны статические моменты относительно координатных плоскостей Оху, Oxz, Oyz; обозначим их соответственно M_xy, M_xz, M_yz. Повторяя рассуждения, получим следующие формулы для координат ξ, η, ζ центра тяжести неоднородного тела, плотность которого задается функцией δ(х, у, z), занимающего область Ω:

, ,

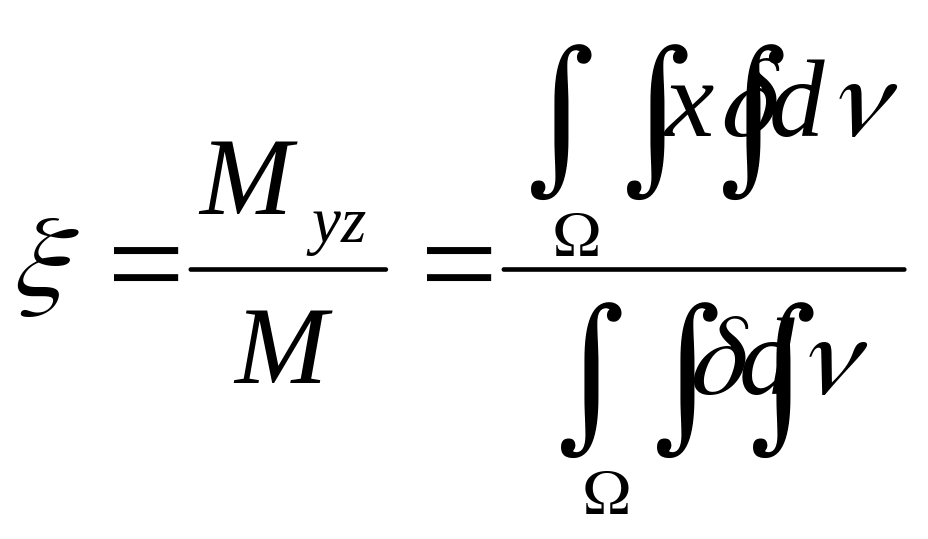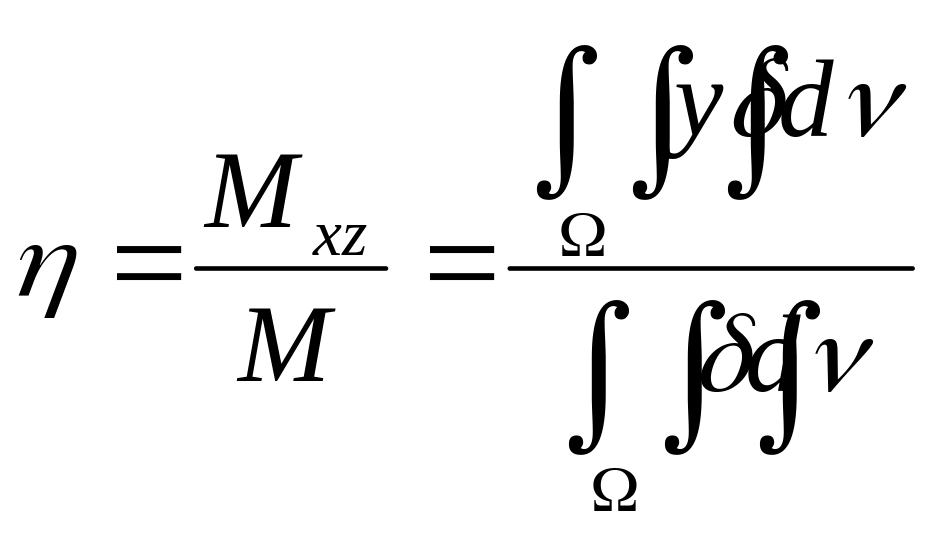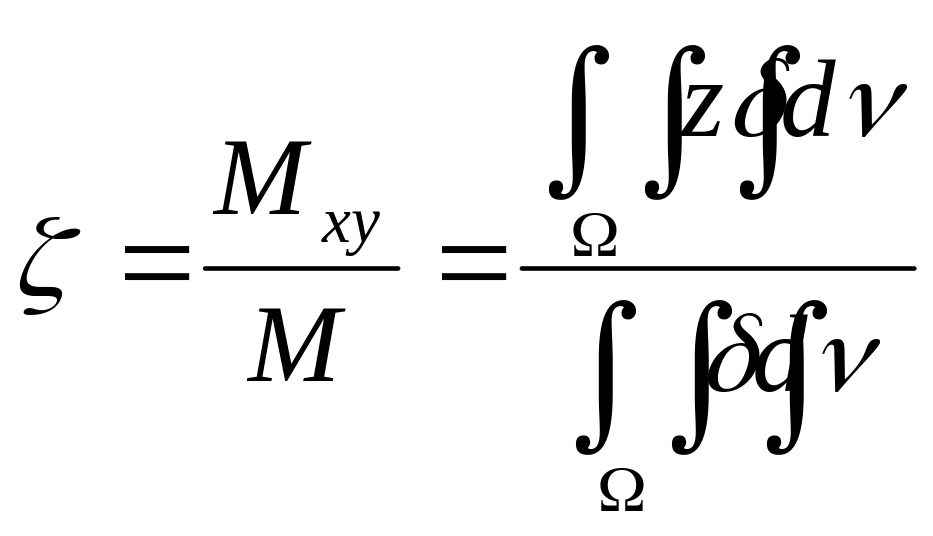
Если тело однородно, т.е. δ = const, то формулы упрощаются:

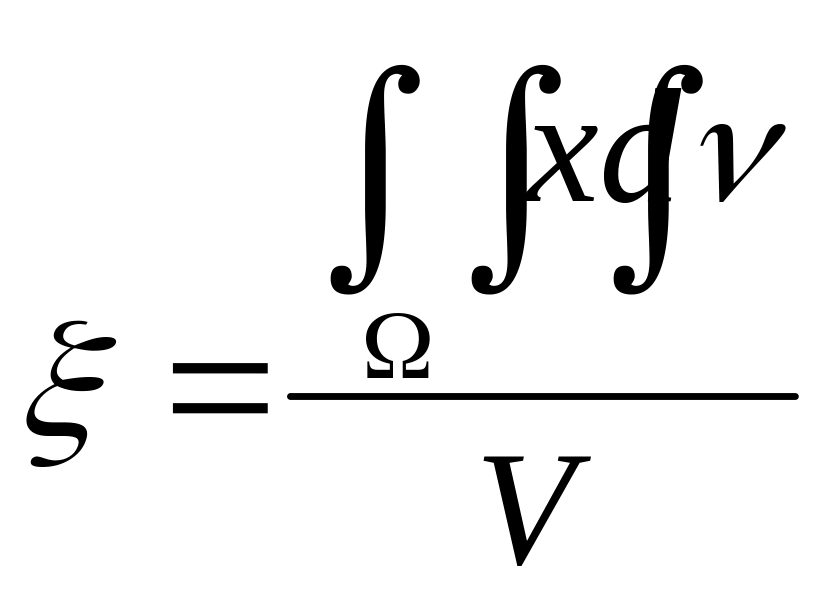
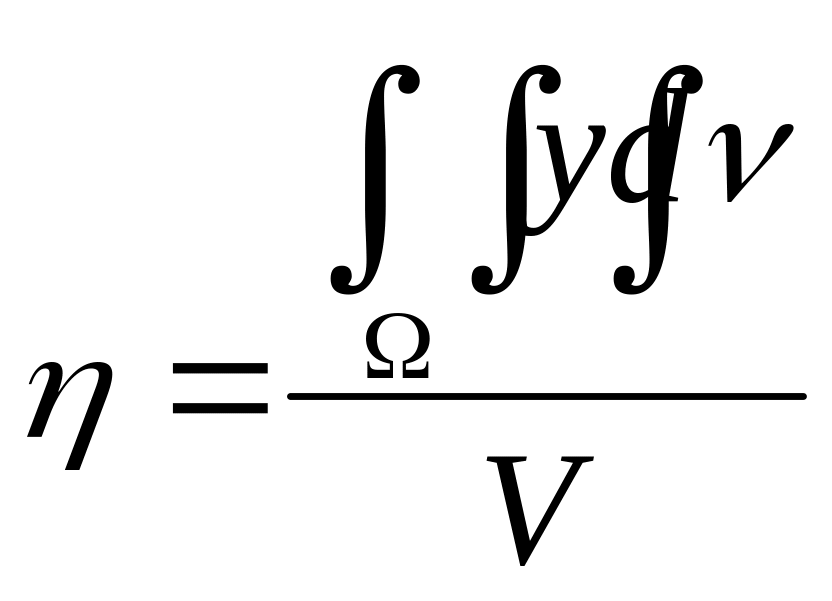
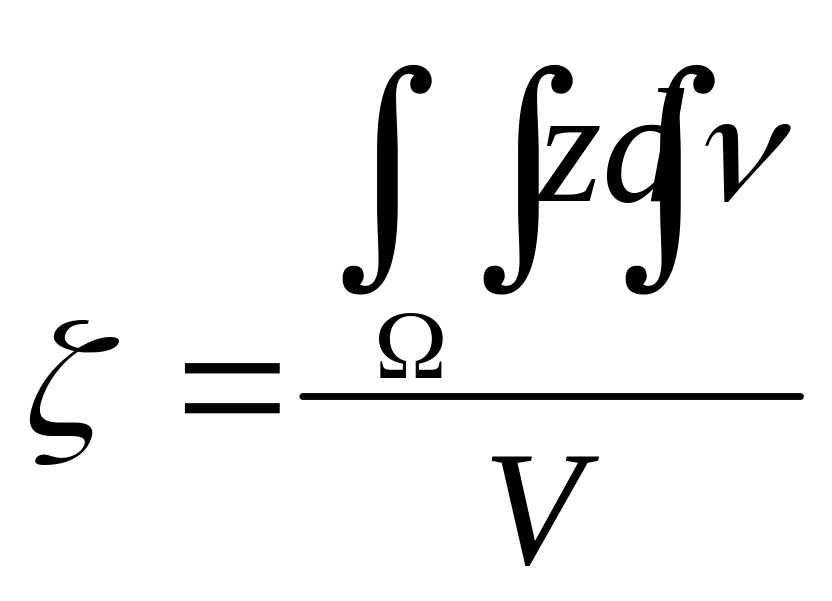
где V – объём тела.

Пример 15. Найдём центр тяжести однородного полушара Ω:

, .

Две координаты центра тяжести (ξ и η) равны нулю, ибо полушар симметричен относительно оси Оz (тело вращения с осью Оz).

Интеграл удобно вычислить, перейдя к сферическим координатам:

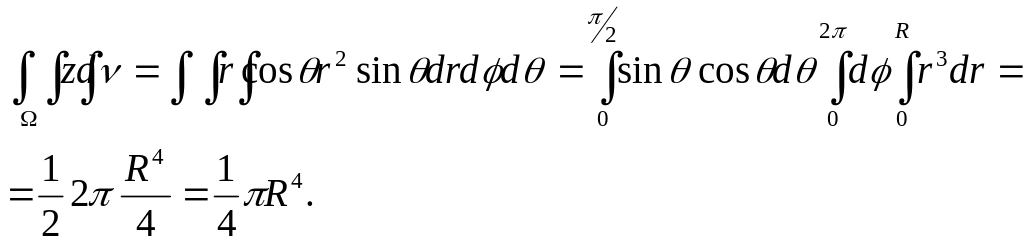
Так как объём полушара равен , то

.

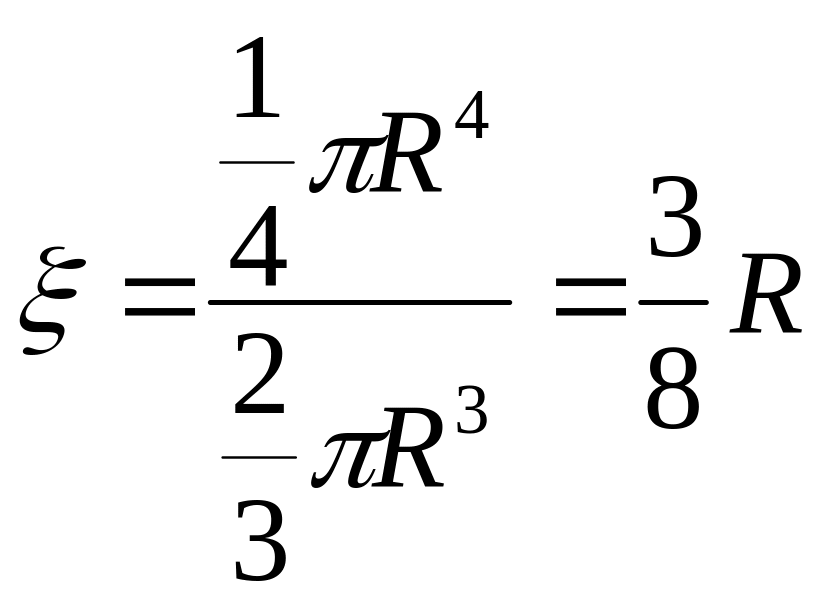Перейдём к вычислению моментов инерции тела относительно координатных осей. Так как квадраты расстояний от точки Р(х, у, z) до осей Ox, Oy, Oz соответственно равны х² + у², х² +z², x² + у², то полагая для простоты δ = 1, получим следующие формулы:

Аналогично плоскому случаю интегралы

называются центробежными моментами инерции. Для полярного момента инерции формула имеет вид

.

Если тело неоднородное, то в каждой формуле под знаком интеграла будет находиться дополнительный множитель δ(x, y, z) – плотность тела в точке Р.

Пример 16. Вычислим полярный момент инерции однородного шара радиуса R. В этом случае очень удобно перейти к сферическим координатам. Будем иметь

где М – масса шара.

Так как для сферы моменты инерции относительно осей координат, очевидно, равны между собой, то, учитывая, что I_x + I_y + I_z = 2I₀, получим

.

Моменты инерции тела относительно оси играют важную роль при вычислении кинетической энергии тела при его вращении около соответствующей оси.

Пусть тело Ω вращается около оси Oz с постоянной угловой скоростью ω. Найдём кинетическую энергию J, тела. Как известно, кинетическая энергия точки измеряется величиной , где m – масса точки, а ν – величина её скорости. Кинетическая энергия системы точек определяется как сумма кинетических энергий отдельных точек, а кинетическая энергия тела – как сумма кинетических энергий всех частей, на которые оно разбито. Это обстоятельство позволяет применить для вычисления кинетической энергии интеграл.

Возьмем какую-нибудь окрестность dv точки Р(х, у, z) тела Ω. Величина линейной скорости ν точки Ρ при вращении около оси Оz равна , и значит, кинетическая энергия части dv тела Ω выразится так :

,

где δ(P) = δ(х, у, z) – плотность тела в точке Р. Для кинетической энергии всего тела Ω получаем

,

т.е.

.

Кинетическая энергия тела, вращающегося около некоторой оси с постоянной угловой скоростью, равна половине квадрата угловой скорости, умноженной на момент инерции тела относительно оси вращения.

Модуль 11. Криволинейные и поверхностные интегралы

1. Криволинейные интегралы

1.1. Криволинейный интеграл первого типа (по длине дуги)

Пусть в некоторой области D плоскости хоу (см. рис. 1) задана непрерывная функция f(x, y) и гладкая незамкнутая кривая L между точками А, В.

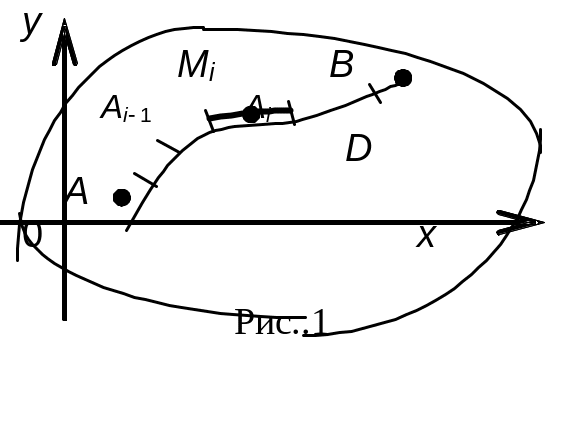
Составим интегральную сумму по уже известному алгоритму. Разобьём кривую L точками А = А₀, А₁, ..., А_п = В

на п произвольных участков l_i, обозначив через l_i длину i–го участка кривой между точками А_i1, A_i, где I = 1, 2, …,п.

В каждом i-том участке выберем произвольно точку M_i = (_i, _i) и подсчитаем в ней значение функции f_i = f(M_i).

Просуммировав произведения f_i  l_i по всем i = 1, 2, …, п, получим интегральную сумму

.

Предел этой интегральной суммы, если он существует и не зависит от типа разбиения дуги L и способа нахождения точек M_i, где i = 1, 2, …, п, называется криволинейным интегралом первого типа от функции f(x, y), взятым по кривой L, и обозначается

где d = maxl_i.

Этому интегралу можно придать вполне определённый физический смысл: если в каждой точке дуги L задана переменная плотность (х, у) — функция точки, то можно подсчитать массу материальной дуги АВ: .

Сравните с задачей о вычислении массы неоднородного стержня, приводящей к понятию определённого интеграла (см. [3]).

Основные свойства криволинейного интеграла первого типа

 Криволинейный интеграл первого типа не зависит от направления пути интегрирования:

 Интеграл от суммы (разности) функций равен сумме (разности) интегралов от каждого слагаемого по тому же пути интегрирования:

 Константа выносится за знак интеграла:

где

 Свойство аддитивности: если путь интегрирования L разбить на участки L₁, L₂ …, L_n, то интеграл по всей дуге равен сумме интегралов по участкам L_i, где i = 1, 2, …, n:

 Формула для вычисления длины дуги (если f(М) = 1 для всех точек кривой L):

где l — длина дуги L.

Как вычислить криволинейный интеграл?

Представим уравнение кривой L в параметрической форме

Направление установлено произвольно (одно из двух возможных). Функции непрерывны вместе со своими производными . Функция f(x, y), определённая в каждой точке кривой, сводится к функции одной переменной t:

Дифференциал дуги вычисляем по формуле

Записываем формулу для вычисления криволинейного интеграла

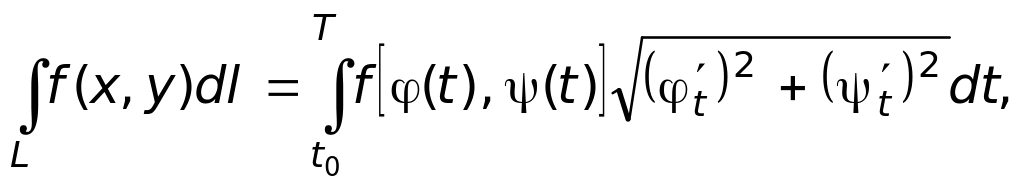
где правая часть равенства — определённый интеграл по переменной t.

В случае пространственной кривой

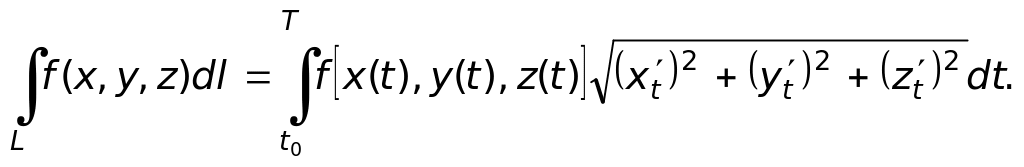
Таким образом, чтобы вычислить криволинейный интеграл по кривой L от функции f(x, y), необходимо свести его к определённому интегралу по аргументу t. Для этого уравнение линии L записывают в параметрической форме и переводят всё подынтегральное выражение к выбранной переменной, начальное и конечное значения которой соответствуют начальной и конечной точкам дуги L выбранного направления; дифференциал dl подсчитывают по формуле (2). В случае трёхмерного пространства используют формулы (3) – (4).

Пример 1. Вычислить массу неоднородной дуги АВ: у² = 2х с плотностью , .

Решение. Запишем уравнение АВ в параметрическом виде.

Пусть у = t. Тогда

Функция (х, у) примет вид

Найдём dl:

Вычислим искомую массу по формуле (13.1):

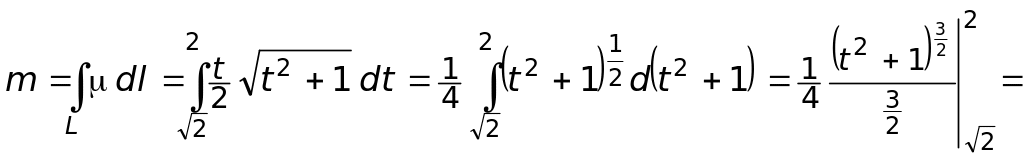
Пример 2. Вычислить где L – линия пересечения поверхностей z = x.

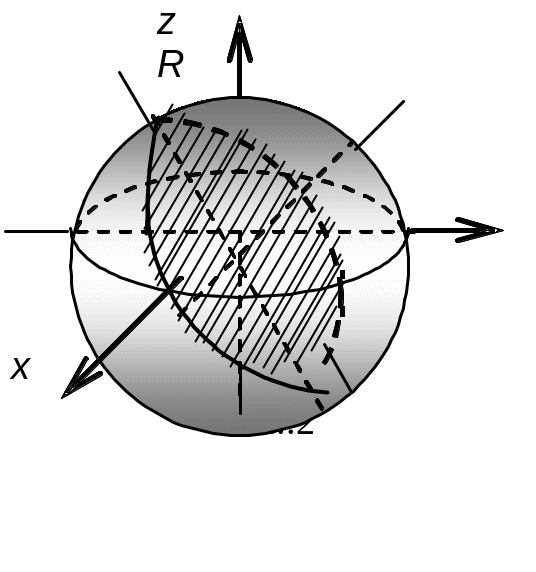
Решение. Кривая представляет собой пересечение сферы и плоскости – это окружность

(см. рис. 2).

В качестве параметра выберем х = t. Из равенства z = х следует z = t. Из уравнения сферы найдём у:

Итак, параметрические уравнения линии интегрирования L:

Пределы интегрирования по аргументу t находим из условия существования функции у:

Составляем дифференциал дуги по формуле (3), для чего найдём производные

Подынтегральная функция примет вид

Переводим криволинейный интеграл в определённый по формуле (4) и вычисляем его:

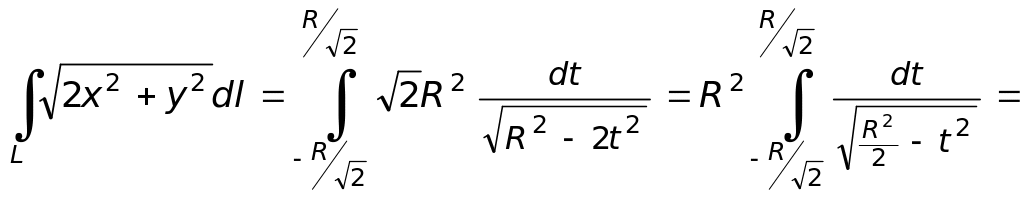
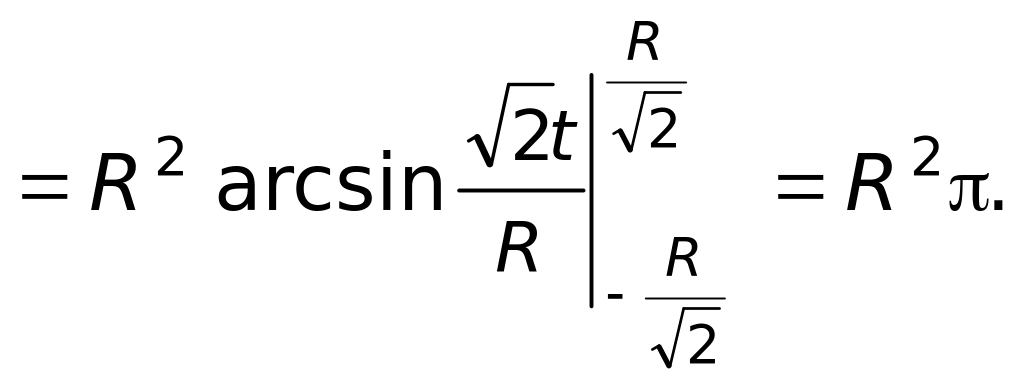
Пример 3. Найти длину астроиды

Решение. Воспользуемся формулой

В нашем случае

Поскольку кривая симметрична относительно осей координат, то

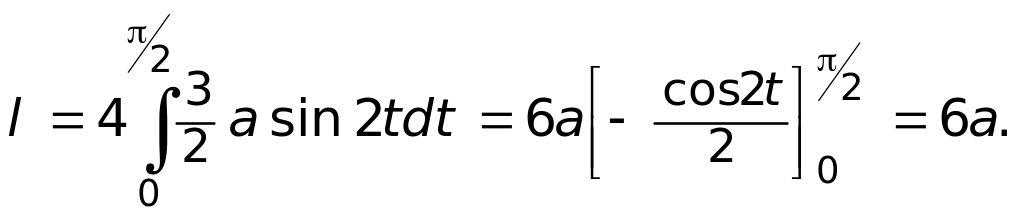
Пример 4. Вычислить массу лемнискаты (см. рис. 3) с плотностью в каждой точке, равной расстоянию её до начала координат.

Решение. В нашем случае

Для вычисления интеграла удобнее воспользоваться полярными координатами, где

Тогда функция плотности уравнение кривой примет вид

,

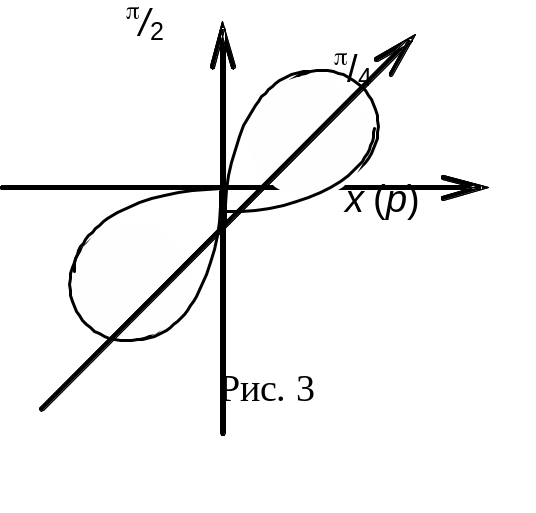
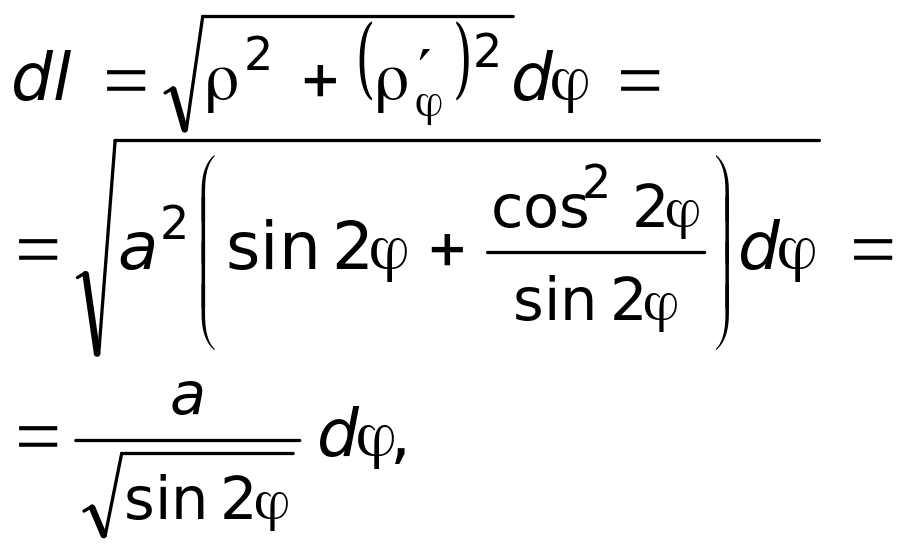
или

Теперь запишем полностью интеграл, используя симметрию кривой: