2.3. Вычисления тройных интегралов в цилиндрических координатах.

Отнесём область Ω к системе цилиндрических координат (r, , z), в которой положение точки Μ в пространстве определяется полярными координатами (r, ) её проекции Ρ на плоскость Оху и её аппликатой (z). Выбирая взаимное расположение осей координат, как указано на рис. 31, установим связь, между декартовыми и цилиндрическими координатами точки М, а именно:

x = rcos,

y = rsin,

z = z

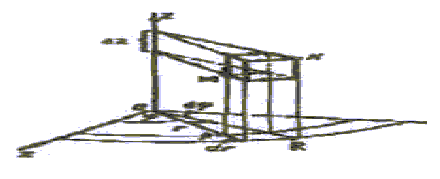
Рис.31

Разобьём область Ω на частичные области ν, тремя системами координатных поверхностей: r = const,  = const, z = const, которыми будут соответственно круговые цилиндрические поверхности, осью которых является ось Oz, полуплоскости, проходящие через ось Oz, и плоскости, параллельные плоскости Оху. Частичными областями ν, служат прямые цилиндры ΜΝ (рис. 31). Так как объём цилиндра ΜΝ равен площади основания, умноженной на высоту, то для элемента объёма получаем выражение

Преобразование тройного интеграла к цилиндрическим координатам производится совершенно аналогично преобразованию двойного интеграла к полярным. Для этого нужно в выражении подынтегральной функции f(x, y, z) переменные x, y, z заменить по формулам (20) и взять элемент объёма равным r dr d dz.

Получим

Если, в частности, f(x, y, z) = 1, то интеграл выражает объём V области Ω

Вычисление тройного интеграла в цилиндрических координатах приводится к интегрированиям по r, по , и по z на основании тех же принципов, что и в случае декартовых координат. В частности, если областью интегрирования служит внутренность цилиндра r  R, 0  z  h, то пределы трехкратного интеграла постоянны и не меняются при перемене порядка интегрирования:

2.4. Вычисление тройных интегралов в сферических координатах

Отнесём теперь область интегрирования Ω к системе сферических координат (r, , ). В этой системе координат положение точки Μ в пространстве определяется её расстоянием r от начала координат (длина радиуса-вектора точки), углом θ между радиусом-вектором точки и осью Oz и углом  между проекцией радиуса-вектора точки на плоскость Оху и осью Ох (рис. 32). При этом θ может изменятся то 0 до π а  – от 0 до 2π.

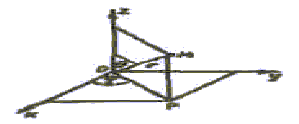
Рис.32

Связь между сферическими и декартовыми координатами легко устанавливается. Из рис. 32 имеем

и .

Отсюда x = r sin cos, y = r cos sin, z = r cos. (21)

Разобьём область Ω на частичные области ν_i тремя системами координатных поверхностей: r = const,  = const, θ = const, которыми будут

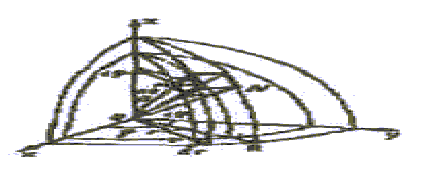
Рис.33

соответственно сферы с центром в начале координат, полуплоскости, проходящие, через ось Oz, и конусы с вершиной в начале координат и с осями, совпадающими с одной из полуосей Оz. Частичными областями ν_i служат «шестигранники» (рис. 33). Отбросив бесконечно малые высших порядков, будем рассматривать шестигранник ΜΝ как прямоугольный параллелепипед с измерениями, равными: dr по направлению полярного радиуса, r dθ по направлению меридиана, r sinθ d по направлению параллели. Для элемента объёма мы получим тогда выражение

Заменив в тройном интеграле х, y, z пo формулам (21) и взяв элемент объёма равным полученному выражению, будем иметь

.

Особенно удобно применение сферических координат в случае, когда область интегрирование Ω – шар с центром в начале координат или шаровое кольцо. Например, в последнем случае, если радиус внутреннего шара R₁, а внешнего R₂, пределы интегрирования следует расставить так:

.

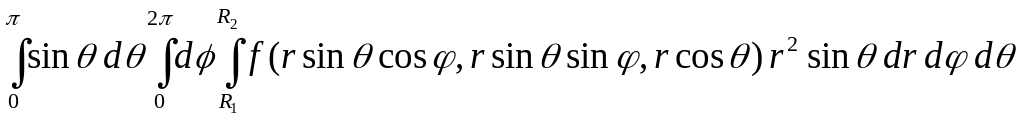Если Ω – шар, то нужно положить R₁= 0.

Пример 14.

Вычислим объём шара радиуса R. В этом случае подынтегральную функцию надо взять равной 1, и мы получим