2.2. Вычисление тройных интегралов в декартовых координатах.

Вычисление тройного интеграла , может быть осуществлено посредством ряда последовательных интегрирований. Мы ограничимся описанием соответствующих правил.

Пусть дан тройной интеграл от функции f(x, y, z)

,

причем область Ω отнесена к системе декартовых координат Oxyz, Разобьём область интегрирования плоскостями, параллельными координатным плоскостям. Тогда частичными областями будут параллелепипеды с гранями, параллельными плоскостям Оху, Oxz, Oуz. Элемент объёма будет равен, произведению дифференциалов переменных интегрирования dv = dx dy dz.

В соответствии с этим будем писать

Установим теперь правило для вычисления такого интеграла.

Будем считать, что область интегрирования Ω имеет вид, изображенный на рис. 27.

Опишем цилиндрическую поверхность с образующей, перпендикулярной к плоскости Оху. Она касается области Ω вдоль некоторой линии L, которая делит поверхность, ограничивающую область, на две части: верхнюю и нижнюю. Уравнением нижней поверхности пусть будет z ·= z₁(x, y), уравнением верхней z = z₂ (x, y).

Построенная цилиндрическая поверхность высекает из плоскости Оху плоскую область D, которая является ортогональной проекцией пространственной области Ω на плоскость Оху, при этом линия L проектируется в границу области D.

Будем производить интегрирование сначала по направлению оси Oz. Для этого функция f(x, y, z) интегрируется по заключенному в Ω отрезку прямой, параллельной оси Oz и проходящей через некоторую точку Р (х, у) области D (на рис. 27 отрезок α β ). При данных x и у переменная интегрирования z будет изменяться от z₁ (x, у) – аппликаты точки «входа» (α) прямой в область Ω, до z₂(x, y) – аппликаты точки «выхода» (β) прямой из области Ω.

Результат интегрирования представляет собой величину, зависящую от точки Ρ (x, у); обозначим её через F(x, у):

При интегрировании х и у рассматриваются здесь как постоянные. Мы получим значение искомого тройного интеграла, если возьмём интеграл от функции F(x, y) при условии, что точка Ρ (x, у) изменяется по области D, т.е. если возьмём двойной интеграл

Таким образом, тройной интеграл I может быть представлен в виде

Приводя, далее, двойной интеграл по области D к повторному и интегрируя сначала по у, а затем по х, получим

где у₁(х) и y₂(х) – ординаты точек «входа» в область D и «выхода» из неё прямой х = const (в плоскости Оху), а а и b – абсциссы конечных точек интервала оси Ох, на который проектируется область D.

Мы видим, что вычисление тройного интеграла по области Ω производится, посредством трёх последовательных интегрирований.

Формула (19) сохраняется и для областей, имеющих цилиндрическую форму, т.е. ограниченных цилиндрической поверхностью с образующими, параллельными оси Oz, а снизу и сверху поверхностями, уравнения которых соответственно z = z₁ (х, у) и z = z₂ (х, у) (рис. 28).

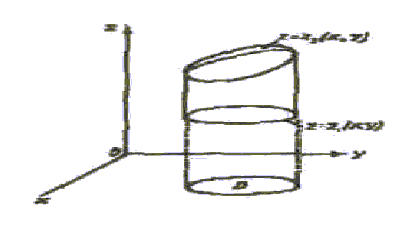
Рис.28

Если областью интегрирования служит внутренность параллелепипеда с гранями, параллельными координатным плоскостям (рис. 29), то пределы интегрирования постоянны во всех трёх интегралах :

В этом случае интегрирование можно производить в любом порядке, пределы интегрирования будут при этом сохраняться.

Если же в общем случае менять порядок интегрирования (т.е., скажем, интегрировать сначала по направлению оси Оу, а затем по области плоскости Oxz), то это приведёт к изменению порядка интегрирования в тройном интеграле и к изменению пределов интегрирования по каждой переменной.

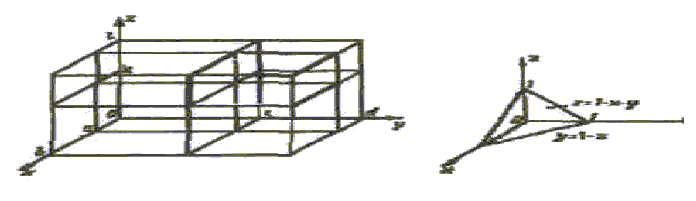
Рис.29 Рис.30

Пример 13. Вычислим тройной интеграл

где Ω – область, ограниченная координатными плоскостями x = 0, y = 0, z = 0 и плоскостью x + у + z = 1 (пирамида, изображённая на рис.30). Интегрирование по z совершается от z = 0 до z = 1 - x - у. Поэтому, обозначая проекцию области Ω на плоскость Оху через D, получим

Расставим теперь пределы интегрирования по области D – треугольнику, уравнения сторон которого х = 0, у = 0, x+ у = 1: