1.6. Вычисление площади поверхности.

Пусть требуется вычислить площадь поверхности, ограниченной линией Г (рис.23); поверхность задана уравнением z == f(x, y) где функция f(x, y) непрерывна и имеет непрерывные частные производные. Обозначим проекцию линии Г на плоскость Оху через L. Область на плоскости Оху, ограниченную линией L, обозначим D.

Разобьём произвольным образом область D на n элементарных площадок ΔS₁, ΔS₂, …, ΔS_n. В каждой площадке ΔS_i возьмём точку Ρ_i (ξ_i ; η_i).

Точке P_i будет соответствовать на поверхности точка M_i (ξ_i ; η_i ; f(ξ_i ; η_i)). Через точку М_i проведём касательную плоскость к поверхности. Уравнение её примет вид

На этой плоскости выделим такую площадку Δσ_i которая проектируется на плоскость Оху в виде площадки ΔS_i. Рассмотрим сумму всех площадок .

Предел σ этой суммы, когда наибольший из диаметров площадок Δσ_i – стремится к нулю, мы будем называть площадью поверхности, т.е. по определению положим

Займёмся теперь вычислением площади поверхности. Обозначим через γ_i угол между касательной плоскостью и плоскостью Оху.

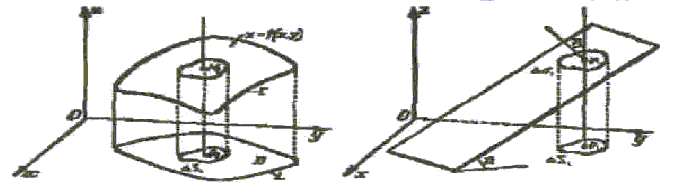
Рис.23 Рис.24

На основании известной формулы аналитической геометрии можно написать (рис.24) ΔS_i = Δσ_icos γ или

Угол γ_i есть в то же время угол между осью Oz и перпендикуляром к плоскости Оxy. Поэтому на основании уравнения и формулы аналитической геометрии имеем

.

Следовательно,

.

Подставляя это выражение в формулу (13), получим

.

Так как предел интегральной суммы, стоящей в правой части последнего равенства, по определению представляет собой двойной интеграл

, то окончательно получаем

Это и есть формула, по которой вычисляется площадь поверхности z = f(x, y).

Если уравнение поверхности дано в виде x = μ(y, z) или в виде у = χ (x, z), то соответствующие формулы для вычисления поверхности имеют вид

где D^’ и D^’’ – области на плоскостях Oyz и Oxz, в которые проектируется данная поверхность.

Пример 11. Вычислить поверхность σ сферы

x² + y² + z² = R²

Решение: вычислим поверхность верхней половины сферы (рис.25). В этом случае

, .

Следовательно, подынтегральная функция примет вид

Область интегрирования определяется условием . Таким образом, на основании формулы (15) будем иметь

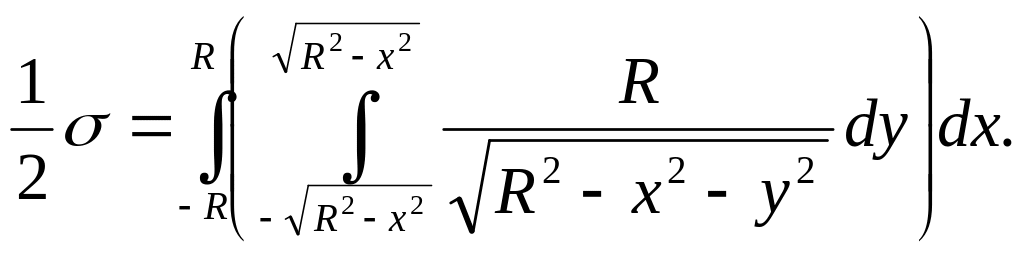
Для вычисления полученного двойного интеграла перейдём к полярным координатам. В полярных координатах граница области интегрирования определяется уравнением ρ = R. Следовательно,

Пример 12. Найти площадь той части поверхности цилиндра

х² + y² = а², которая вырезается цилиндром x² + z² = а².

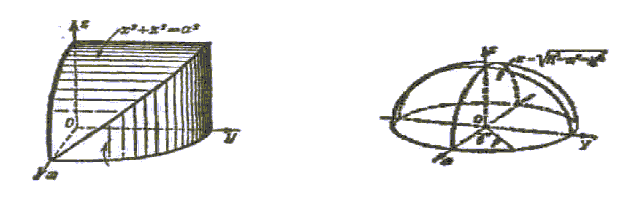
Рис.26 Рис.25

Решение: на рис. 26 изображена часть искомой поверхности. Уравнение поверхности имеет вид , поэтому

, .

Область интегрирования представляет собой четверть крута, т.е. определяется условиями , .

Следовательно,

2. Тройной интеграл

2.1. Масса неоднородного тела

Рассмотрим тело, занимающее пространственную область Ω (рис. 27), и предположим, что плотность распределения массы в этом теле является непрерывной функцией координат точек тела: Δ = δ(x, y, z).

Единица измерения плотности – кг/м³

Рис.27

Разобьем тело произвольным образом на n частей; объёмы этих частей обозначим Δν₁, Δν₂, …, Δν_n. Выберем затем в каждой части по произвольной точке P_i(x_i , y_i , z_i). Полагая, что в каждой частичной области плотность постоянна и равна её значению в точке P_i, мы получим приближённое выражение для массы всего тела в виде суммы

Предел этой суммы при условии, что n   и каждое частичное тело стягивается в точку (т.е. что его диаметр) стремится к нулю, и даст массу Μ тела

.

Сумма называется n-й интегральной суммой, а её предел – тройным интегралом от функции δ(x, y, z) по пространственной области Ω.

К вычислению тройного интеграла, помимо определения массы тела, приводят и другие задачи. Поэтому в дальнейшем мы будем рассматривать тройной интеграл

где f(x, y, z) – произвольная непрерывная в области Ω функция.

Терминология для тройных интегралов совпадает с соответствующей терминологией для двойных интегралов. Точно так же формулируется и теорема существования тройного интеграла.

Свойства двойных интегралов, полностью переносятся на тройные интегралы. Заметим только, что если подынтегральная функция f(x, y, z) тождественно равна 1, то тройной интеграл выражает объем V области Ω: .

Поэтому свойства сформулированы следующим образом.

Свойство 6. Если функция f(x, y, z) во всех точках области интегрирования Ω удовлетворяет неравенствам

то

,

где V – объём области Ω.

Свойство 7. Тройной интеграл равен произведению значения подынтегральной функции в некоторой точке области интегрирования на объём области интегрирования, т.е.

.