1.3. Вычисление двойных интегралов в полярных координатах

Для вычисления двойного интеграла мы пользовались до сих пор системой декартовых координат. Отнесём теперь плоскость к системе полярных координат r, φ и предположим, как обычно, что полюс лежит в начале координат и полярная ось совпадает с осью абсцисс. Тогда декартовы координаты точки выражаются через полярные по формулам

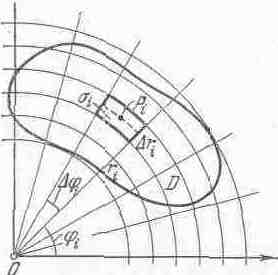
рис.15

x = r cos φ, у = r sin φ.

Разобьём область интегрирования D на частичные области σ_i двумя системами координатных линий: r = const, φ = const. Этими линиями будут соответственно концентрические окружности с центром в полюсе и лучи, исходящие из полюса (рис. 15). При этом частичными областями σ_i будут криволинейные четырехугольники, ограниченные дугами концентрических окружностей и их радиусами. Площадь Δσ_i области σ_i будет

Или где

есть средний радиус между r_i, и r_i + Δr_i .

Пусть дана функция f(x, у), непрерывная в области D. Составим для неё интегральную сумму, разбивая область D на частичные области Δσ_i, и выбирая в качестве произвольных точек Р_i (x_i , y_i) областей σ_i точки, лежащие на средних окружностях радиуса r_i т.е. полагая

.

Тогда

Так как в правой части стоит интегральная сумма для функции f(r cos φ, r sinφ)r по переменным r и φ, то, переходя к пределу, получим

.

Это равенство является формулой преобразования двойного интеграла от декартовых координат к полярным. Выражение называется элементом площади в полярных координатах.

Правило преобразования двойного интеграла к полярным координатам.

Для того чтобы преобразовать двойной интеграл в декартовых координатах в двойной интеграл в полярных координатах, нужно x и у в подынтегральной функции заменить соответственно через r cos φ и r sin φ, а произведение dxdy заменить произведением r dr dφ.

Вычисление двойного интеграла в полярной системе координат, также как и в декартовой, сводится к последовательному интегрированию по переменным r и φ. Укажем правило расстановки пределов.

Пусть полюс не содержится внутри области интегрирования D, заключенной между лучами φ=φ₁ и φ = φ₂, и координатные линии φ = const встречают её границу не более чем в двух точках (рис. 16а). Область может также иметь вид, изображенный на рис. 16б.

Полярные уравнения кривых ADC и АВС пусть будут r = r₁ (φ) и r = r₂ (φ).

Интегрируя сначала по r в пределах его изменения при постоянном φ, т.е. от r₁ (φ) до r₂ (φ), а затем по φ от φ₁ до φ₂, получим

.

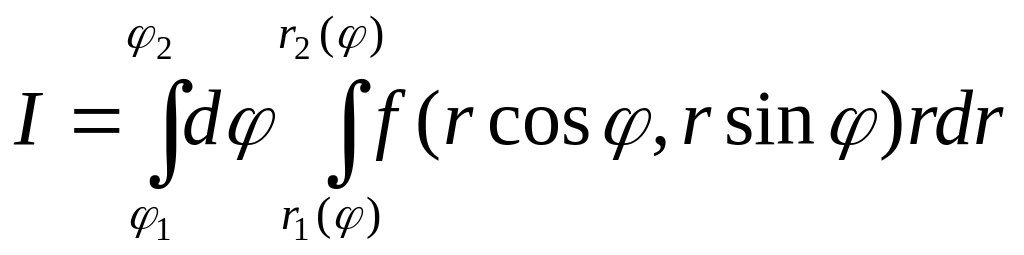Интегрирование в обратном порядке, т.е. сначала по φ, а потом по r, обычно не встречается.

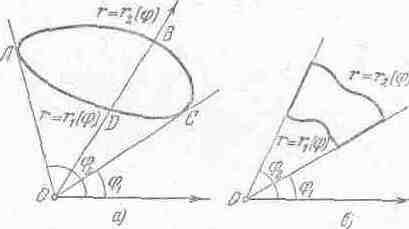
Рис.16.

В частном случае, когда областью интегрирования служит часть кругового кольца , пределы интегрирования постоянны по обеим переменным:

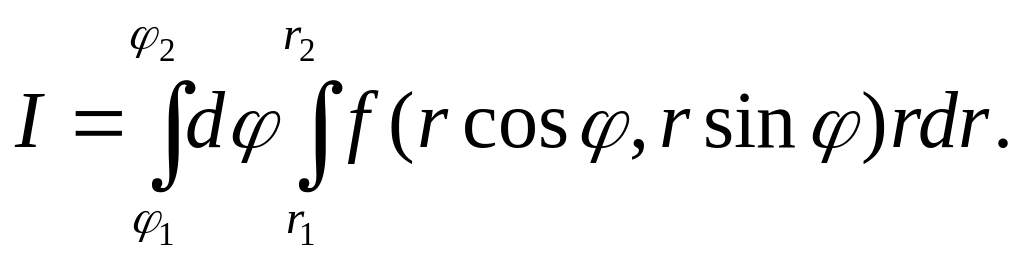
Пример 7. Расставим пределы интегрирования в полярных координатах, если область D – круг (рис. 17). Переходя к полярным координатам, получим уравнение окружности в виде r = a cos φ. Здесь r₁ (φ) = 0 и r₂ (φ) = a cos φ. Пределы изменения по φ от до . Поэтому

.

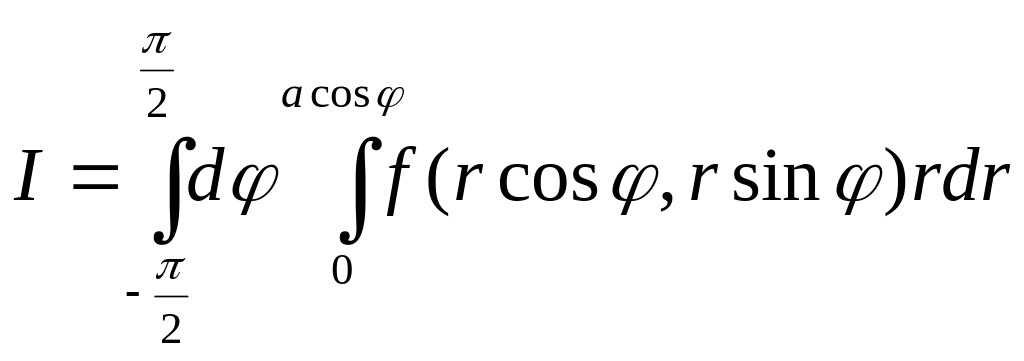Пример 8. Вычислим объём V общей части шара радиуса а и кругового цилиндра радиуса при условии, что центр шара лежит на

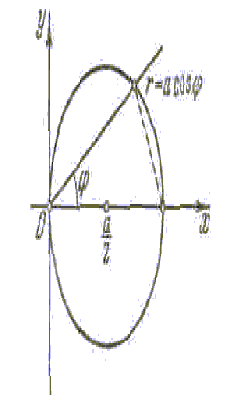
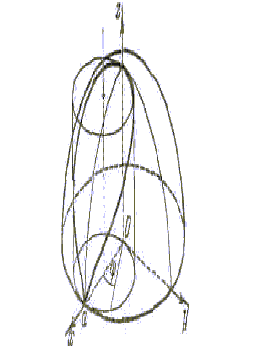
Рис. 17 Рис. 18.

поверхности цилиндра. В силу симметрии измеряемого тела относительно плоскостей Оху и Охz мы можем вычислить четвертую часть объёма, заключенную в первом координатном угле.

Имеем ,

где D – полукруг, являющийся половиной основания цилиндра.

Здесь очень удобно преобразовать двойной интеграл к полярным координатам. В соответствии с правилом преобразования имеем

Так как полярное уравнение полуокружности, ограничивающей область D, есть r = a cos φ (см. пример 7), то, интегрируя сначала по r, а затем по φ, найдём

.

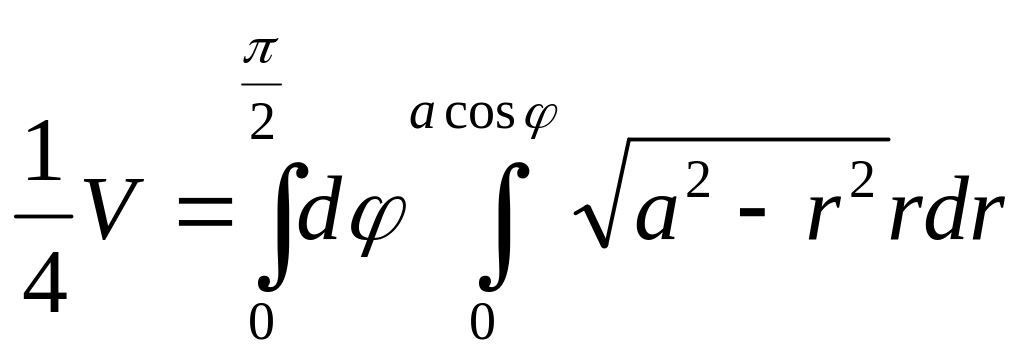Находя внутренний интеграл, получаем

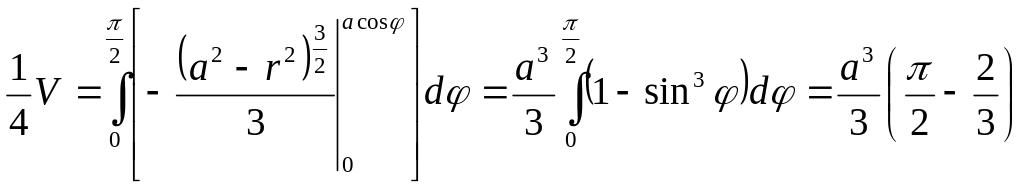
Отсюда

.