шпаргалка

Сопротивление материалов.

Под действием внешних сил реальные твёрдые тела деформируются, при этом возникают внутренние силы и моменты которые стремятся вернуть тело в исходное состояние.

Исчезающая деформация называется упругой, неисчезающая пластичной.

Напряжением называется интенсивность внутренних сил в сечении тела.

Растяжение и сжатие.

Гипотеза плоских сечений : все поперечные сечения бруса недеформируются, следовательно, нормальные силы равномерно распределены по сечению.

Интенсивность это нормальные напряжения на площадь.

Д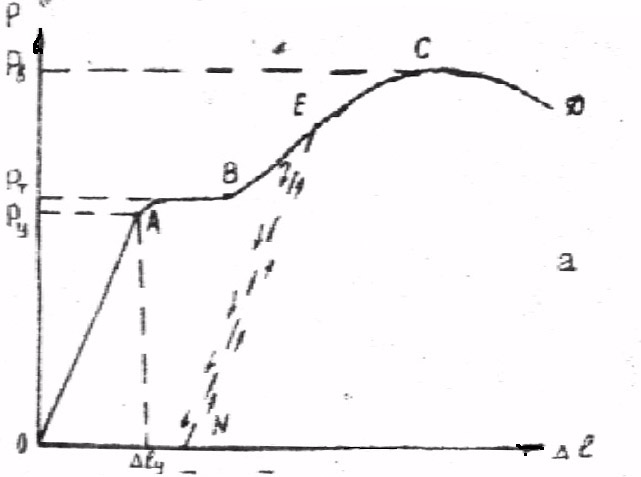 иаграмма растяжения материалов

рис.2.

ОА- зона линейной упругости, для которой характерны:

• линейная связь между силой Р и удлинением l

• при разгрузке образца он полностью восстанавливает свои размеры

Зону линейной упругости характеризуют два параметра:

• Предел упругости _у – есть наибольшее напряжение, при котором в результате разгрузки не появляется остаточных деформаций.

• Модуль Юнга Е – есть коэффициент пропорциональности в линейном законе Гука при растяжении =Е

АВСД – зона пластичности, для этой зоны характерно образование остаточных деформаций при разгрузке образца.

АВ – участок пластического течения , характеризуется пределом текучести

где F – первоначальная площадь поперечного сечения.

ВС – участок упрочнения, заканчивается точкой С , соответствующей образованию на образце шейки. Напряжение в образце, соответствующее этой точке называется пределом прочности материала.

На участке СД величина силы падает с ростом деформаций.

₀=   ,  - коэфф. Пуассона.(=0 – пробка, =0.3 –металлы)

Условие прочности

 - нормальное напряжение, N- продольная сила,

А – площадь поперечного сечения.

Коэфф. концентрации напряжений

_R – предел выносливости материала- это такое напряжение которое материал выдерживает при неограниченом числе нагружений.

Сдвиг.

Сдвиг производят две равные паралельные противоположно направленные силы действующие на небольшом расстоянии друг от друга. Принимаем что сила Q распределена в сечении равномерно, тогда возникают касательные напряжения = ^Q/_A ; где А –площадь сечения.

Деформации : абсолютная - а ; относительная tg   = ^A/_h

Таким образом при сдвиге мы имеем угловую деформацию, при растяжении линейную.

Закон Гука для сдвига: напряжения пропорциональны деформациям. = G  ; где G модуль упругости второго рода.

- где GA жёсткость при сдвиге.

Условие прочности для сдвига .

Характеристики плоских сечений.

Статический момент площади – есть взятая по всей площади сечения сумма произведений элементарных площадок на их расстояния до соответствующей оси, по всей площади сечения.

Выражения статических моментов входят в выражения координат центров тяжести.

Таким образом статические моменты площади относительно центральных осей равны нулю.

Моменты инерции площади осевые и полярные есть сумма произведений элементарных площадок на квадрат их расстояния до соответствующей оси или точки.

Моменты инерции площади аналогичны моментам инерции массы и к ним применима теорема Штейнера.Моменты инерции простейших сечений.

1.Прямоугольник.

h

Чтобы найти момент инерции относительно центральной оси применим теорему Штейнера.

2.Круг.

Полярный момент инерции.

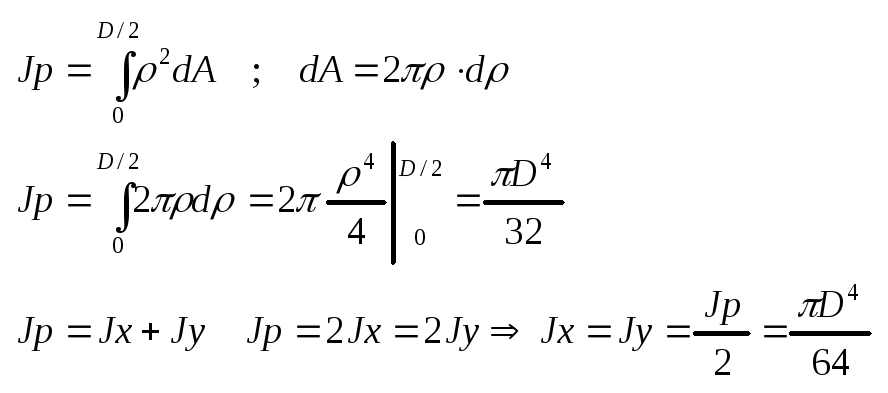
3.Кольцо.

Т.е. Момент инерции кольца мало отличается от момента инерции круга с такимже наружным диаметром.

Кручение бруса круглого поперечного сечения.

Кручением называется такой вид нагружения, при котором к брусу прикладываются две равные и противоположно направленные пары сил, действующие в плоскостях, перпендикулярных оси бруса.

Внутренний крутящий момент М_к в общем случае равен сумме моментов всех сил, децствующих по одну сторону от сечения, относительно продольной оси бруса. Нагружение бруса крутящим моментом сопровождается поворотом поперечных сечений бруса друг относительно друга на некоторый угол , называемый углом закручивания. Одновременно с этим образующая на цилиндрической поверхности бруса поворачивается относительно начального положения на угол  , называемый углом сдвига.

Угол сдвига характеризующий угловую деформацию

Если взять любую элементарную площадку сечения, расположенную на расстоянии  от оси вращения,то для неё относительный угол сдвига _= , по закону Гука для сдвига =G тогда напряжение сдвига на площадка dA будет направлено перпендикулярно радиусу и равно =G.

Элементарная внутренняя сила на площадке dF= dA= G dA.

Момент элементарной силы относит. оси бруса dM= dF=G² dA

Сумма таких элементарных моментов, взятая по всему сечению А, должна равнятся внешнему скручивающему моменту

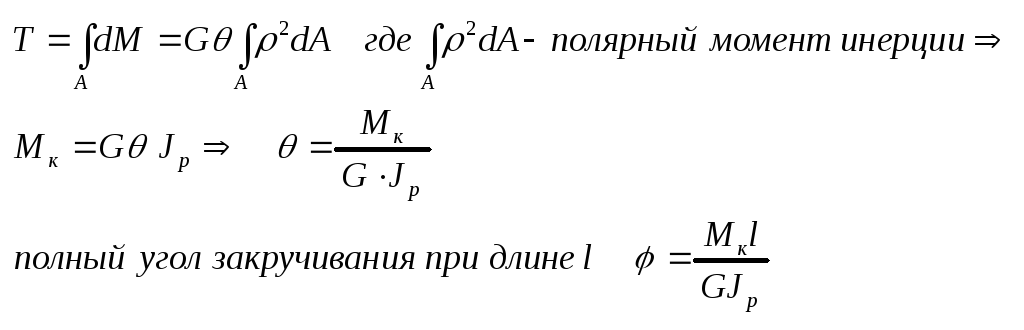
GJ_p- жёсткость при кручении. Подставив выражение угла закручивания в формулу напряжений получим _=М_к/J_p т.е. касательные напряжения при кручении в любой точке сечения пропорциональны расстоянию от этой точки до оси кручения.

Обозначим отношение J_p/r через W_р тогда максимальные напряжения можно выразить формулой _макс=М_к / W_p. Величина W_p называется полярным моментом сопротивления.

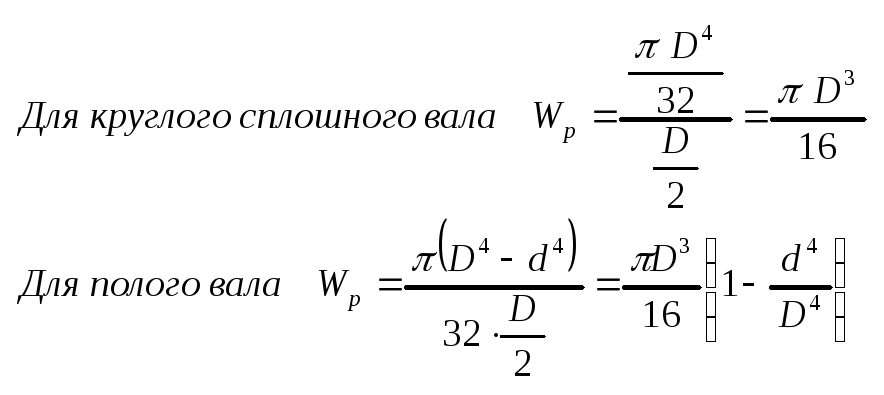
Условие прочности на кручение круглого вала

Условие расчета на жёсткость

Изгиб.

При действии сил или пар сил, перпендикулярных к продольной оси бруса и лежащих в плоскостях, проходящих через эту ось, происходит изгиб бруса. Если изгибающие моментыявляются единственными силовыми факторами, действующими в поперечных сечениях бруса, то изгиб называется «чистым», если наряду с изгибающими моментами возникает поперечное усилие Q то изгиб называют «поперечным». Изгибающий момент численно равен сумме моментов всех сил действующих по одну сторону от сечения.

Правило знаков.

Поперечная сила считается положительной если сумма проекций на ось “y” слева от сечения направлена вверх, а справа от сечения вниз, и наоборот.

+ М - М

Условия равновесия выделенного элемента балки

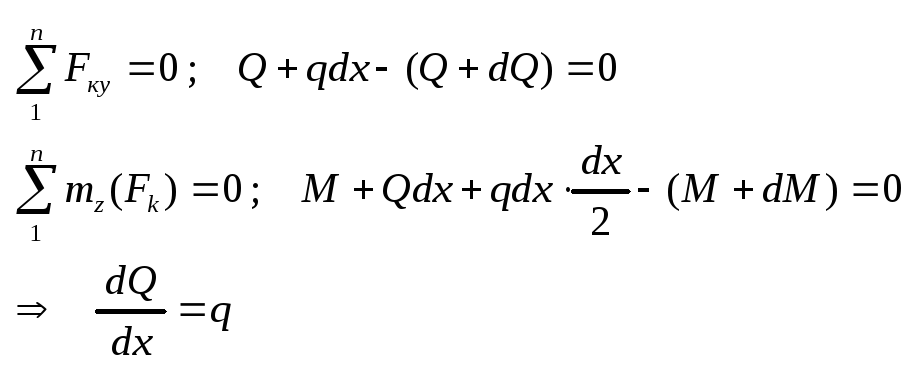
производная от поперечной силы по абциссе сечения равна интенсивности нагрузки в данном сечении.

Пренебрегая бесконечно малой второго порядка, имеем

Производная от изгибающего момента по абциссе сечения равна поперечной силе в этом сечении. Сопоставив две последние формулы

Вторая производная от изгибающего момента по абциссе равна интенсивности распределённой нагрузки.

Напряжения в сечениях балки.

Приняв гипотезу плоских сечений можно считать что поперечные сечения балки не деформируются, а только поворачиваются относительно друг друга на определённый угол. Значит на внешней стороне изогнутой балки волокна растянуты, а на внутренней сжаты. Следовательно, существует слой который не растянут и не сжат – нейтральный слой. Линия пересечения нейтрального слоя с любым поперечным сечением балки есть нейтральная ось (ось изгиба).

При изгибе балки между двумя сечениями расположенными на бесконечно близком расстоянии друг от друга образуется угол d, а нейтральный слой изогнётся по дуге радиуса . Рассмотрим слой m₁m₂ , расположенный на расстоянии «y” от нейтрального слоя, m₁m₂ / dx – относительная деформация или относительное удлинение . Из подобия треугольников имеем Линейная деформация волокон прямо пропорциональна их расстоянию до нейтрального слоя. По закону Гука => нормальные напряжения при изгибе прямо пропорциональны расстоянию данного слоя до нейтральной оси.

Определим положение нейтрального слоя в балке.

Возьмем элементарную площадку dA , отстоящую от нейтрального слоя на величину «y” . Элементарная нормальная сила на этой площадке Т.к. волокна лежащие выше оси растягиваются, а нижние сжимаются то нормальные напряженияна площадках ниже и выше оси имеют разные знаки и сумма нормальных сил в сечении - нуль.

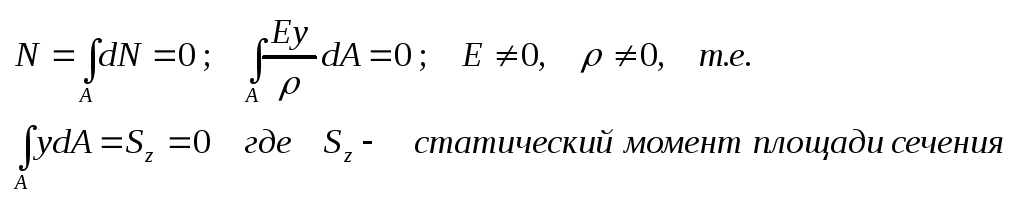
Статический момент равен нулю в том случае если ось, относительно которой момент вычисляется, проходит через центр тяжести сечения. Следовательно , нейтральная ось проходит через центр тяжести сечения.

Нормальные напряжения в слое расположенном на расстоянии “y” от нейтральной оси. Момент элементарной силы

Нормальные напряженияв данном слое волокон прямо пропорциональны расстоянию до этого слоя от нейтральной оси.

Обозначим момент сопротивления изгибу Значения осевых моментов сопротивления длянекоторых сечений.

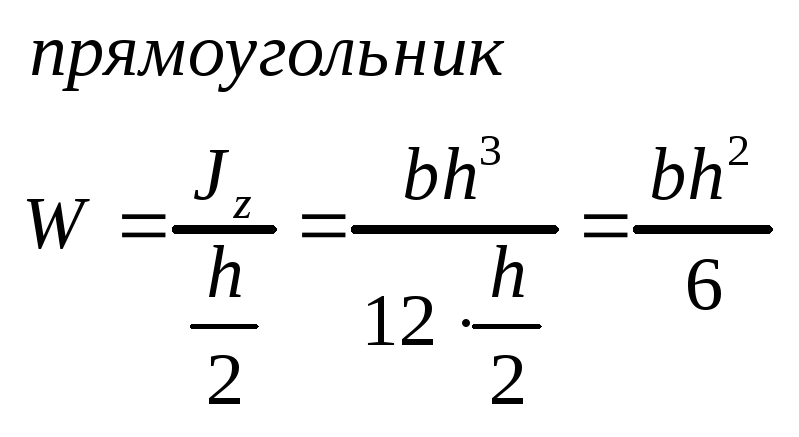
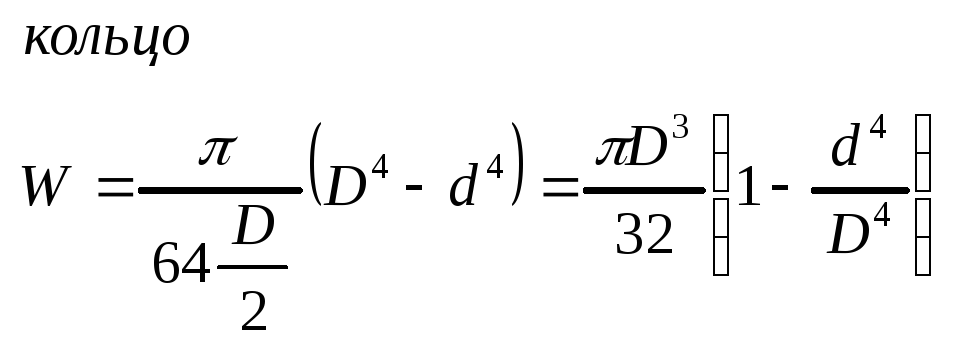
Условие прочности на изгиб _расч<=[].

Деформации при изгибе.

При изгибепрямолинейная ось балки деформируется и приобретает вид некоторой кривой называемой упругой линией. Линейное перемещение центра тяжести сечения по направлению,

перпендикулярному оси балки, называется прогибом. Обозначим эту величину через «y”, Прогиб является функцией продольной координаты x : y = y (x). Угловое перемещение  - это угол на который поворачивается сечение по отношению к своему первоначальному положению. Считая прогибы и углы поворота весьма малыми, можно принять, что tg    = ^dy/_dx.

Пусть балка длиной l , изогнута по дуге окружности .

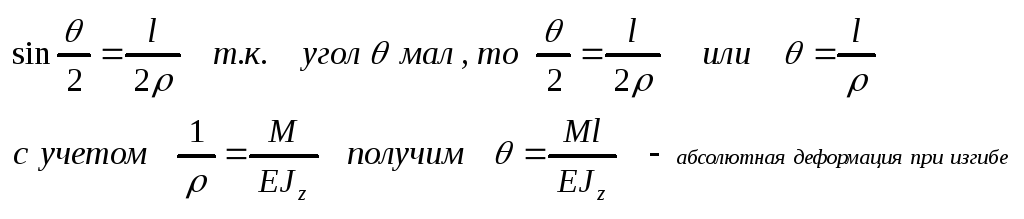При поперечном изгибе момент – величина переменная и значение  получается как интегральная сумма бесконечно малых значений этой величины на участках балки длиной l.

Деформацию балки можно определить по теореме Максвелла-Мора.

Пусть требуется определить прогиб в сечении С некоторой произвольно нагруженной балки. Обозначим искомую величину через у_с. Возьмём такую же балку, нагрузим её в томже сечении силой F=1, а затем сообщим балке прогиб у_с . Работа единичной силы А=1* у_с . Эта работа внешней силыравна внутренней энергии деформации изгиба U при повороте сечения C на угол . Т.к. момент от единичной нагрузки переменен по длине балки, потенциальную энергию U определим как интегральную сумму элементарных величин на длине l. Элементарное значение потенциальной энергии можно определить как работу единичного изгибающего момента при повороте на угол d

М₁ – момент от единичной нагрузки, приложенной в том месте где требуется определить перемещение. М(х) – момент от заданых нагрузок. Если определяют прогиб, то прикладывать следует единичную силу, если угол то единичный момент.

Понятие о сложном напряжённом состоянии и гипотезах прочности.

В процессе работы элементы механических систем могут одновременно испытывать воздействие нескольких разнородных нагрузок. В этих случаях при расчётах на прочность исходят, из принципа независимости действия сил, т.е. считают что если к системе приложено несколько сил , то при малых деформациях можно определить внутренние силы, напряжения и деформации от каждой силы в отдельности, а затем результаты тем или иным способом суммировать. Если в материале возникают только нормальные или только касательные напряжения то их можно суммировать алгеброически.

Объёмное напряжённое состояние материала можно представить как растяжение или сжатие по трём взаимно перпендикулярным направлениям по которым будут действовать три нумерованых в порядке уменьшения главных напряжения. ₁>₂>₃.

По теории наибольших касательных напряжений условие прочности имеет вид ₁-₃<=[], где [] – допускаемое нормальное напряжение при одноосном растяжении.

По теории Мора

Энергетическая теория.