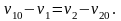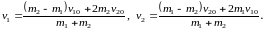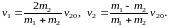Міністерство освіти і науки України

Національний технічний університет України

“Київський політехнічний інститут”

Протокол лабораторної роботи № 1-1 Вивчення законів збереження енергії та імпульсу для зіткнення куль

Виконав:

Студент 1 курсу, ФТІ

Група ФБ-22

Клоченок Р.

Перевірив:

Тараненко Ю.О.

Київ 2013

Робота 1.1. Вивчення законів збереження енергії та імпульсу за зіткнення куль Теоретична довідка

Рухаючись, тіла часто зіткаються одне з одним. При зіткненні обидва тіла де­фор­муються, при цьому та кінетична енергія, що її мали тіла до зіткнення, частково або пов­ністю переходить у потенціальну енергію пружньої деформації і внутрішню енергію тіл. Розрізняють два граничні види удару – абсолютно пружній і абсолютно не­пруж­ній.

Розглянемо ці процеси на прикладі пружнього та непружнього зіткнення в одновимірному просторі. Це значно спростить математичні викладки, не змінюючи суті. Спрощення стосується швидкості, яка в одновимірному просторі є скаляр. Зви­чай­но, в загальному випадку швидкість – це вектор.

Рис. 1.1.

При абсолютно непружному ударі одне тіло прилипає до іншого. При цьому потенціальна енергія деформації не виникає; кінетична енергія повністю або частково перетворюється у внутрішню енергію; після зіткнення обидва тіла рухаються з однаковою швидкістю.

Припустимо, два тіла з масами m₁ і m₂ рухаються назустріч одне одному (рис. 1.1) із швидкостями v₁ і v₂, відповідно. Після непруж­нього зіткнення вони утво­рюють одне тіло масою m₁ + m₂, яке рухається із швидкістю v. Із закону збереження імпульсу:

m1v1 — m2v2 = (m1 + m2)v.

(1)

Звідси знаходимо швидкість тіл після зіт­кнен­ня:

v = (m1v1 — m2v2)/(m1 + m2).

(2)

При непружньому зіткненні має місце лише закон збереження імпульсу. Механічна енергія при цьому не зберігається. Дійсно, повна механічна енергія системи перед зіткненням дорівнює сумі кінетичних енергій кожного з тіл:

EПОЧ .

(3)

Механічна енергія після зіткнення визначається як

EКІНЦ

(4)

При написанні другої рівності в формулі (4) ми скористалися спів­від­но­шен­ням (2). Відновлення механічної енергії зручно характеризувати за допо­мо­гою коефіцієнту К, який визначається як відношення Е_КІНЦ/Е_ПОЧ. Прий­ма­ючи до уваги (3), (4), отримуємо

.

(5)

Формула (5) вказує на те, що коефіцієнт відновлення механічної енергії при непружньому ударі завжди менше одиниці. У випадку, коли одне з тіл, скажімо, перше, до зіткнення було нерухомим (тобто v₁ = 0), К ви­значається лише спів­від­но­шенням мас тіл:

(6)

У випадку рівних мас (m₁ = m₂) та ненульових початкових швидкостей:

(6а)

Рис. 1.2.

і залежить тільки від початкових швидкостей.

Абсолютно пружнім називають удар, при якому механічна енергія системи збе­рі­гається. При пружньому зіткненні тіла спочатку деформуються і їх кінетична енергія переходить у потенціальну енергію пруж­ньої деформації. Потім тіла відновлюють свою форму і відштовхуються одне від одного, при цьому енергія пружньої де­фор­мації знов переходить у кінетичну. Рух тіл після пружнього зіткнення визначається законами збереження імпульсу та кінетичної енергії. Розглянемо цен­траль­не зіткнення двох тіл, що рухаються на­зу­стріч одне одному із швидкостями v₁₀ і v₂₀ (Рис. 1.2). Якщо тіла рухаються тільки по­ступально і не обертаються, то рівняння збе­реження енергії та імпульсу мають вигляд:

.	(7)
.	(8)

де v₁ і v₂ — швидкості тіл після зіткнення і вважається, що після зіткнення ті­ла рухаються вздовж тієї ж прямої, що і перед зіткненням. Перепишемо рівняння (7), (8) у такому вигляді:

,	(7а)
.		(8а)

Порівнюючи (7а) та (8а), приходимо до висновку, що

(9)

З (8а) та (9) легко визначити швидкості обох тіл після зіткнення:

(10)

У випадку, коли перше тіло до зіткнення перебувало у стані спокою (v₁₀ = 0), формула (10) приймає вигляд:

(11)

Формула (11) вказує на те, що при рівних масах (m₁ = m₂) тіла після зіткнення обмінюються швидкостями, тобто після зіткнення друге тіло зупиняється, а перше тіло рухається із швидкістю v₂₀, яку мало друге тіло до зіткнення. Чим більша різниця між масами тіл, тим менша швидкість першого і більша швидкість другого тіла після зіткнення.
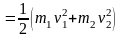
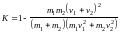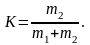
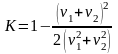
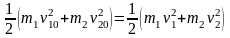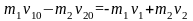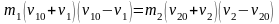