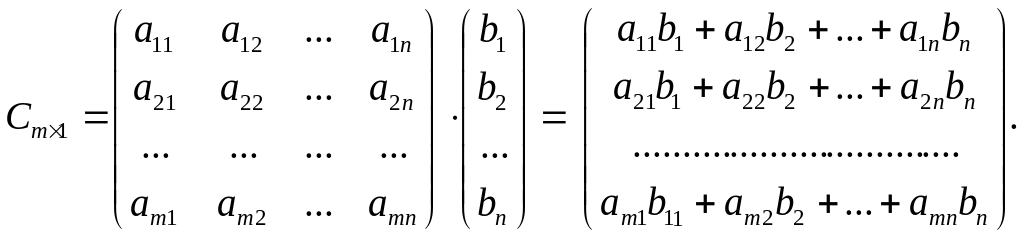Типовой расчет

Разложить вектор ==(k+N-12, 2N-4, 5-N) по системе векторов

₁=(k,-8,9), ₂=(1,2,-1), ₃=(3,-1,1) (k – номер группы студента, N= ).

Сделать проверку.

2. Матрицы и определители

2.1 Основные сведения о матрицах

Матрицей размера m´n называется прямоугольная таблица чисел, содержащая m строк и n столбцов, и обозначается:

Числа (для ), составляющие матрицу, называются элементами матрицы, где i – номер строки, j – номер столбца.

Матрица, состоящая из одной строки называется вектор-строкой, а матрица, состоящая из одного столбца — вектор-столбцом.

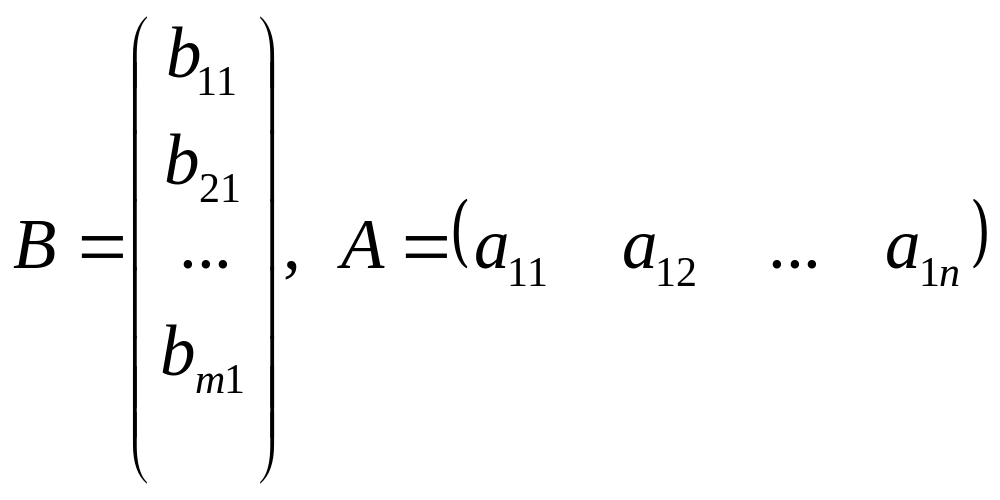
Матрица, все элементы которой равны нулю, называется нуль-матрицей или нулевой матрицей и обозначается:

Матрица называется квадратной n – го порядка, если число ее строк равно числу ее столбцов и равно n:

Элементы матрицы ( ), у которых номер строки равен номеру столбца (i=j), называются диагональными. Эти элементы образуют главную диагональ матрицы. Для квадратной матрицы диагональными элементами являются элементы а₁₁, а₂₂,…, a_nn .

Квадратная матрица, у которой все элементы, находящиеся выше или ниже главной диагонали, равны нулю, называется матрицей треугольного вида:

Квадратная матрица, у которой все недиагональные элементы равны нулю, называется диагональной матрицей и обозначается:

Диагональная матрица, все диагональные элементы которой равны единице, называется единичной матрицей и обозначается:

Две матрицы одинакового размера (m´n) называются равными, если равны их соответствующие элементы: a_ij=b_ij.

2.1.1 Операции над матрицами

1. Умножение матрицы на число.

Умножить матрицу А на некоторое число k - значит умножить каждый ее элемент на это число. В итоге получаем матрицу , элементы которой для :

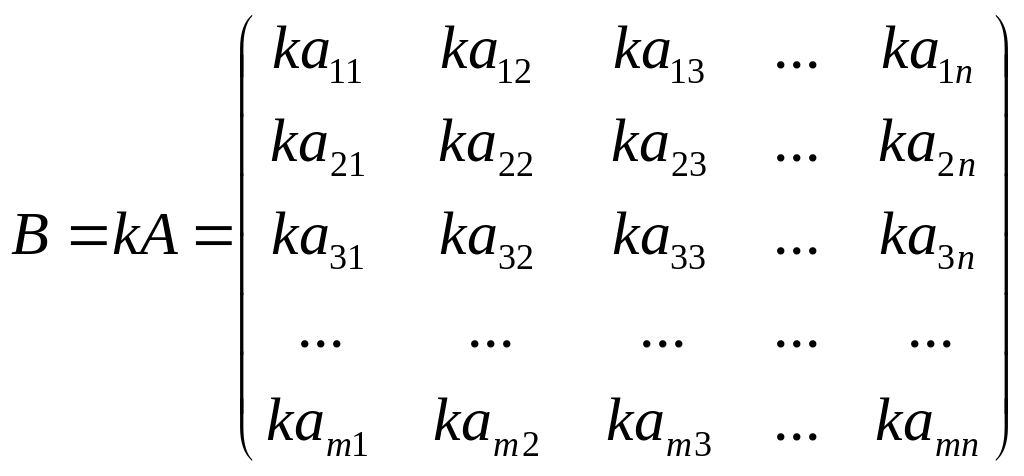
В частности, произведение матрицы А на число 0 равно нулевой матрице А: 0´А =0.

Если k = -1, то матрица - А называется противоположной матрицей для матрицы А.

2. Сложение матриц.

Если А и В — две матрицы одинакового размера m´n , то под их суммой понимается матрица С=А+В, элементы которой равны суммам соответствующих элементов матриц А и В:

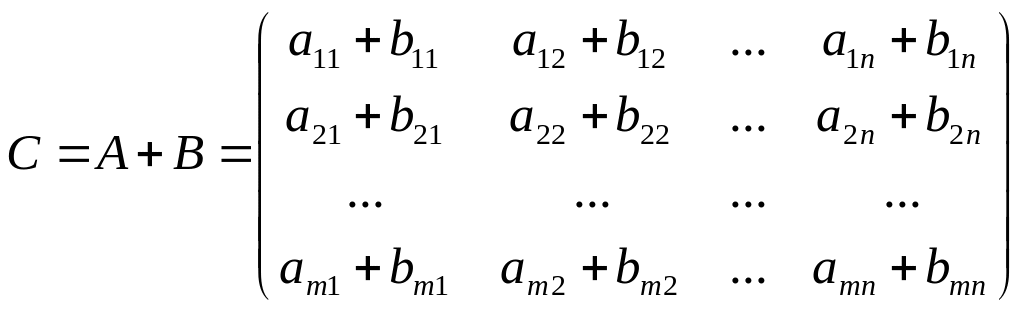
Свойства операций сложения и умножения на число:

• коммутативность операции сложения матриц : А+В = В+А;

• ассоциативность операции сложения матриц: (A+B)+C = A+(B+C);

• дистрибутивность относительно сложения матриц: k(A+B)= kA+kB;

• дистрибутивность относительно сложения чисел: (k+λ)А=kA+λА;

• ассоциативность операции умножения матрицы на число: k(λА)= (kλ)А

3. Вычитание матриц.

Если А и В — две матрицы одинакового размера m´n , то под их разностью понимается матрица С=А+(-1)´В, элементы которой равны суммам элементов матриц А и В, умноженной на число k = -1.

3. Умножение матриц.

Произведение матриц определено только тогда, когда число столбцов матрицы А совпадает с числом строк матрицы В.

Под произведением двух матриц А_mk ´ В_kn понимается матрица С_mn, элементы которой с_ij равны сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В:

для .

Свойства операции умножения:

• ассоциативность операции умножения матриц:

(АВ)C = A(BC);

a(АВ)=(aА)В=А(aВ);

• отсутствие коммутативности операции умножения матриц:

АВ¹ВА

(если АВ=ВА, то матрицы А и В называются перестановочными);

• дистрибутивность операции умножения матриц:

(A+B)C=AС+ВC,

C(A+B) = CA+CB;

Частные случаи перемножения матриц:

1. При перемножении вектор-строки на вектор-столбец получается число:

.

Например: , . .

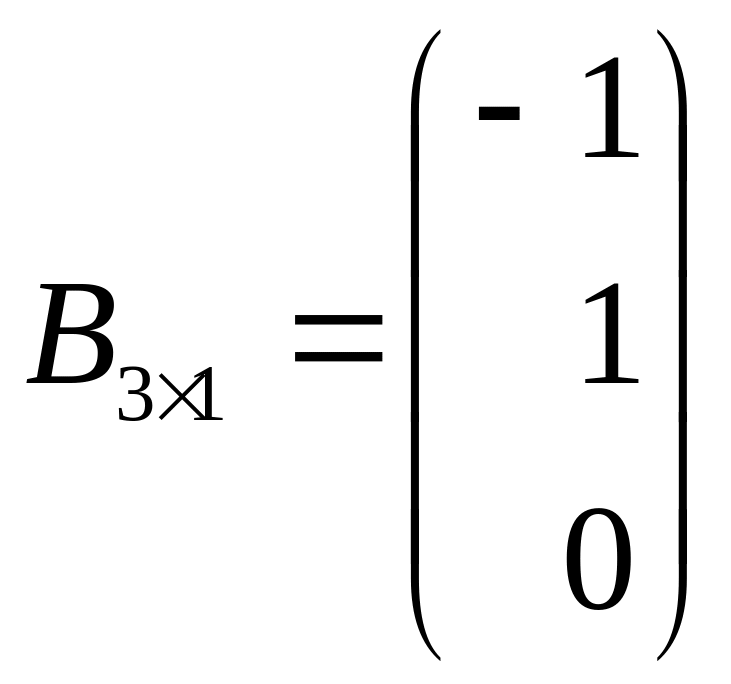2. При перемножении матрицы на вектор получается вектор:

,
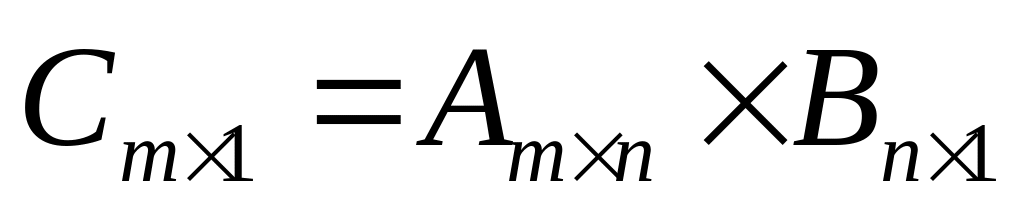
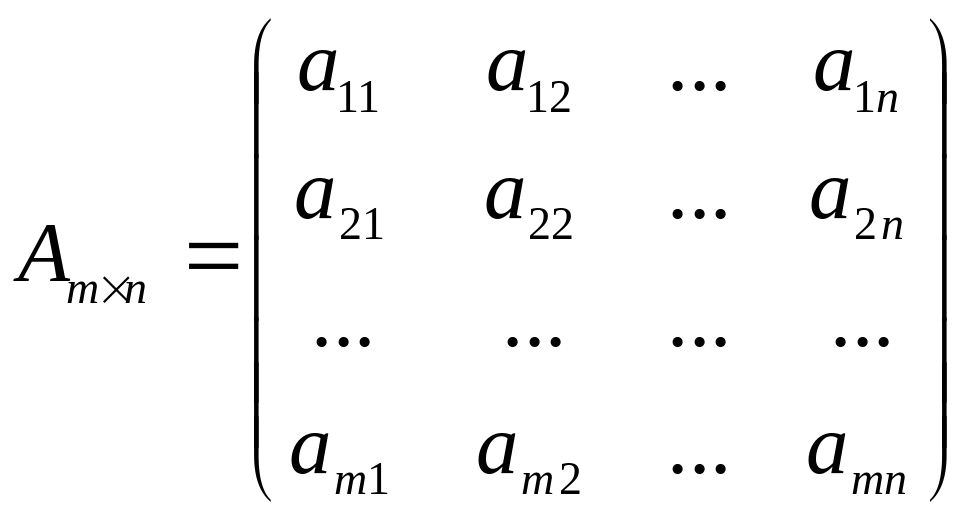