
- •Оглавление
- •Введение
- •Тема 1. N-мерное векторное пространство
- •Тема 2. Матрицы и определители
- •Тема 3. Системы линейных уравнений
- •Тема 4. Системы однородных линейных уравнений
- •Тема 5. Системы линейных неравенств
- •1.1 Векторы и действия над ними
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •1.2 Линейная зависимость векторов
- •1.2.1 Ранг и базис системы векторов
- •1.2.2 Переход от одного базиса к другому Метод замещения
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •1.3 Разложение вектора по базису
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •2. Матрицы и определители
- •2.1 Основные сведения о матрицах
- •2.1.1 Операции над матрицами
- •Умножение матрицы на число.
- •Сложение матриц.
- •Вычитание матриц.
- •Умножение матриц.
- •Возведение в степень матриц.
- •Транспонирование матриц.
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •2.2 Определители (детерминанты) квадратных матриц
- •2.2.1 Основные методы вычисления определителей
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •2.3 Ранг матрицы
- •1. Метод окаймляющих миноров.
- •Метод элементарных преобразований.
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •2.4 Обратная матрица
- •Нахождение обратной матрицы методом замещения
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •3. Системы линейных уравнений
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •4. Системы линейных однородных уравнений
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •5. Линейные неравенства
- •Упражнения
- •Контрольные задания
- •Вопросы для теоретического опроса
- •Список рекомендуемой литературы Основная литература
- •Дополнительная литература
- •Математика Линейная алгебра Методические указания и задания для самостоятельной работы студентов всех специальностей
- •410052, Саратов, ул. Международная, 24
- •410052, Саратов, ул. Международная, 24
Упражнения
1.Найти ранг матрицы:
а)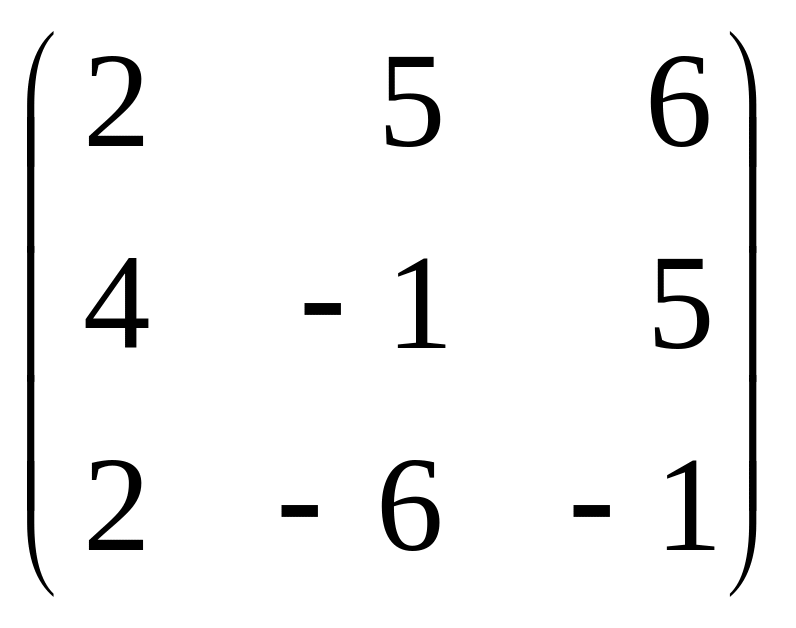 ;
б)
;
б)
 ;
в)
;
в)
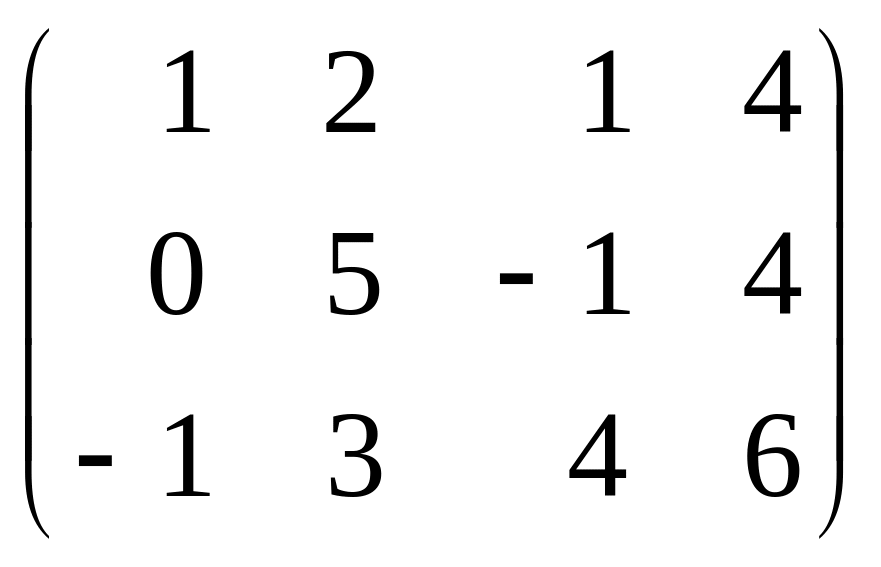 ;
г)
;
г)
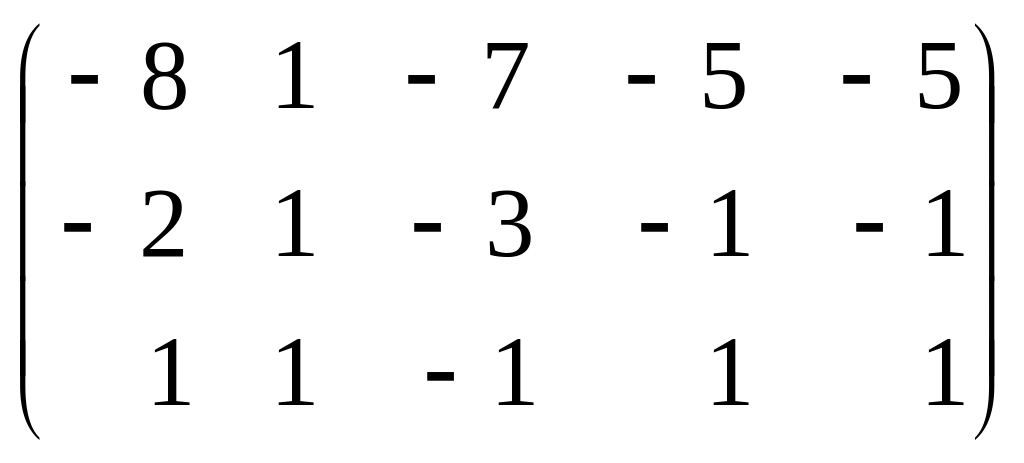
(Ответ: а) r=2; б) r=2; в) r=3; г) r=2.)
2. Найти ранг матрицы:
а)
 ;
б)
;
б)
 ;
в)
;
в)
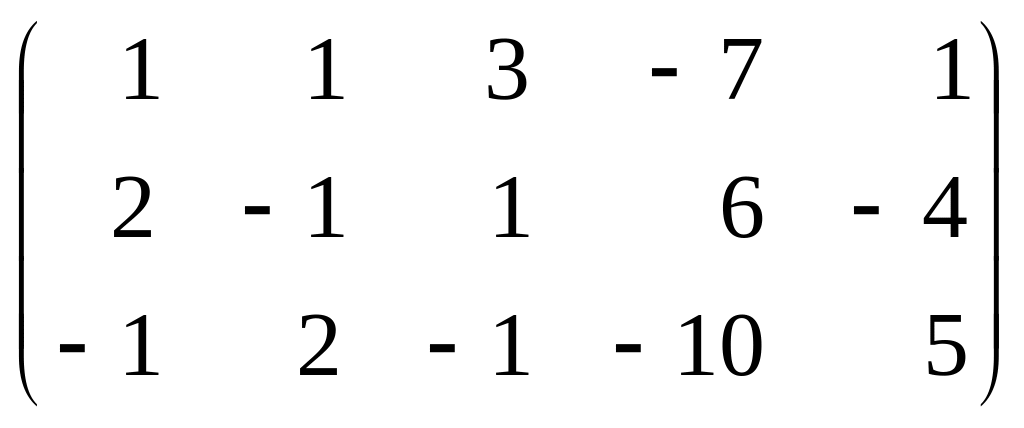 ;
г)
;
г)

(Ответ: а) r=2; б) r=3; в) r=3; г) r=3.)
Контрольные задания
Найти ранг матрицы A методом элементарных преобразований
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Типовой расчет
Дана матрица
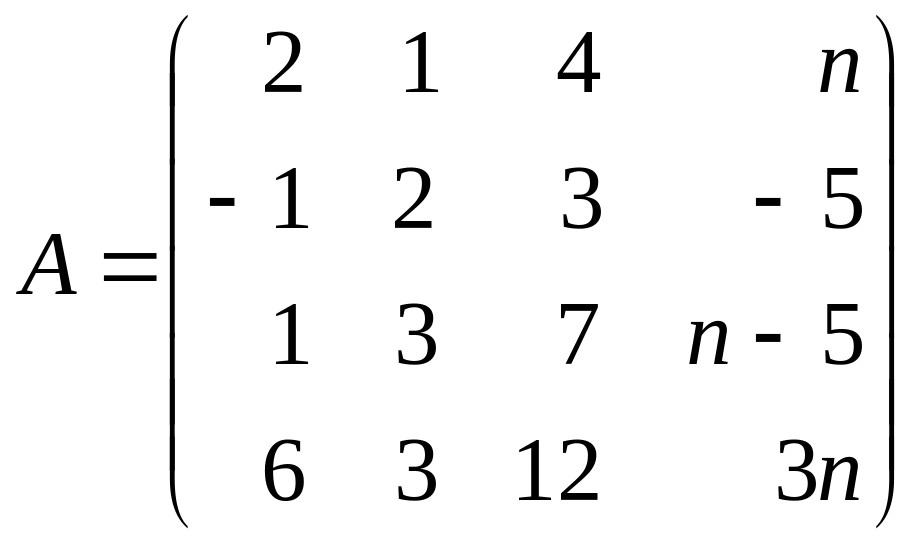 .
.
Найти ранг матрицы A: 1) методом окаймляющих миноров; 2) методом элементарных преобразований; 3) методом замещения.
2.4 Обратная матрица
Матрица А-1 называется обратной для квадратной матрицы А, если выполняются равенства
A A-1 = A-1A = E.
Свойства обратных матриц:
(A-1)-1=А;
(AВ)-1=В-1А-1;
(A-1)′=(А′)-1;
(A-1)m =(Аm)-1.
Матрица А называется
невырожденной или неособенной,
если определитель матрицы не равен нулю
(![]() ),
в противном случае (
),
в противном случае (![]() )–
вырожденной (особенной).
)–
вырожденной (особенной).
Теорема. Квадратная матрица А имеет обратную тогда и только тогда, когда она невырожденная. В этом случае обратную матрицу можно вычислить по формуле:
![]()
где
![]() - присоединенная матрица, элементы
которой равны алгебраическим дополнениям
элементов матрицы А¢,
транспонированной к матрице А.
- присоединенная матрица, элементы
которой равны алгебраическим дополнениям
элементов матрицы А¢,
транспонированной к матрице А.
Для вычисления обратной матрицы необходимо:
найти определитель матрицы А. Если определитель матрицы не равен нулю
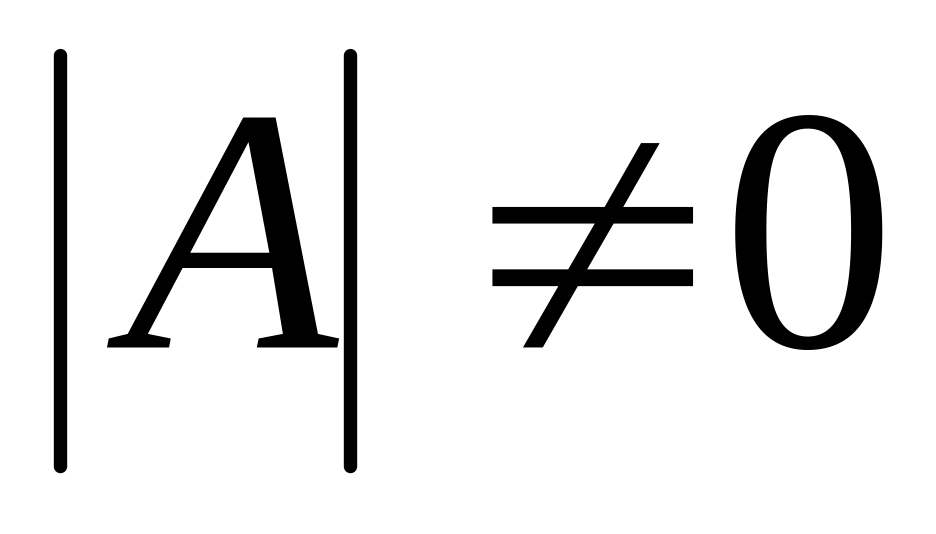 ,
то матрица невырожденная и
обратная матрица существует;
,
то матрица невырожденная и
обратная матрица существует;найти матрицу А¢, транспонированную к матрице А;
найти алгебраические дополнения элементов транспонированной матрицы А¢ и составить присоединенную матрицу
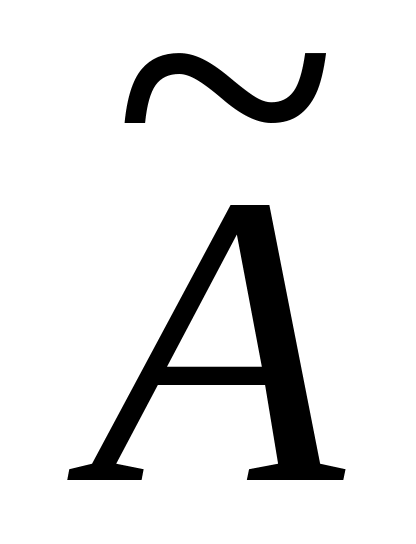 ;
;
вычислить обратную матрицу по формуле: .
Пример. Найти
обратную матрицу к данной
 .
.
Решение.
1. Определитель матрицы А не равен нулю, т.е. матрица невырожденная и обратная матрица существует.

2. Найдем матрицу А¢, транспонированную к матрице А:
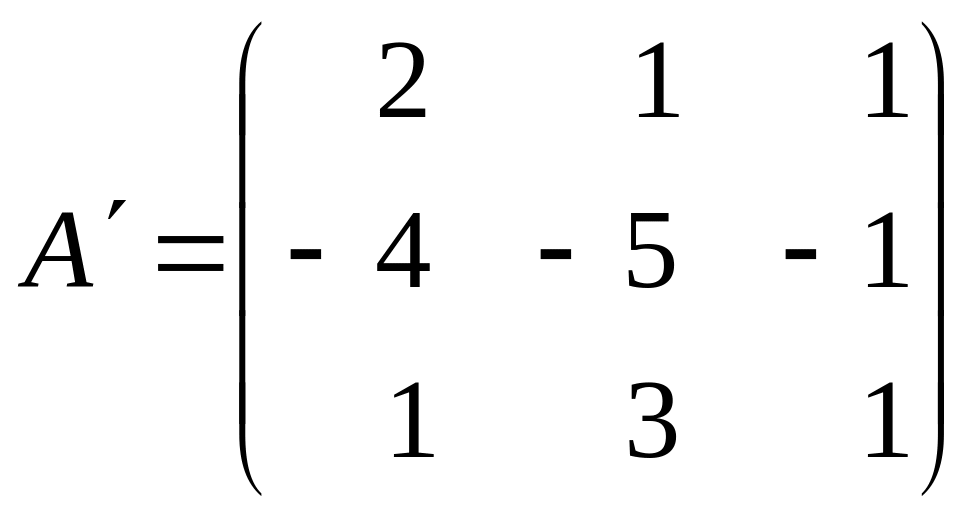
3. Найдем алгебраические дополнения элементов транспонированной матрицы А¢:
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
и составим присоединенную матрицу:
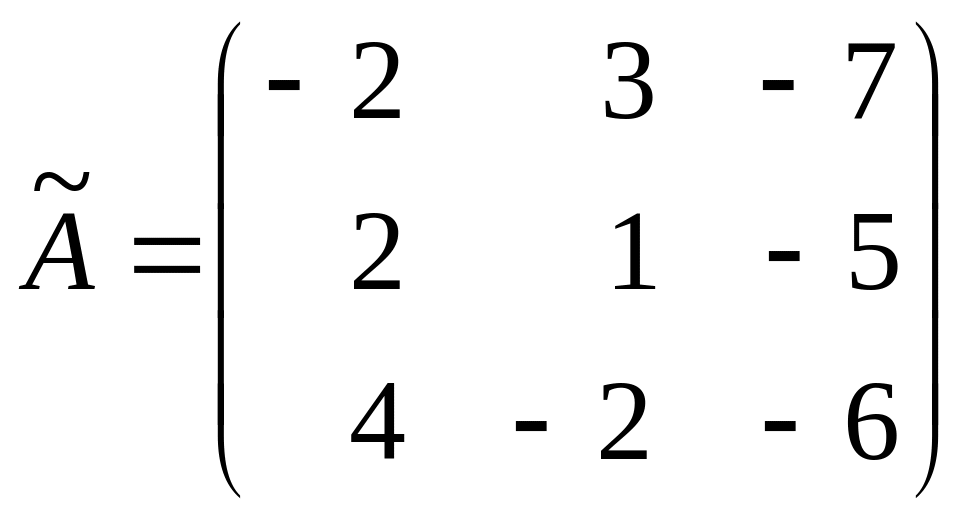 .
.
4. Вычислим обратную матрицу по формуле:
 .
.
Проверим правильность вычислений по формуле A A-1 = A-1A = E.
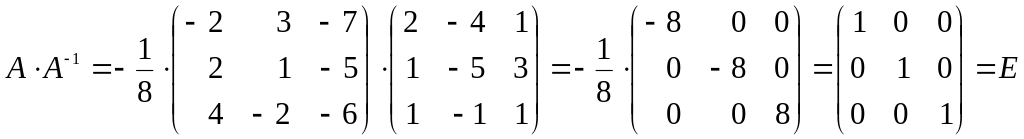 .
.
Нахождение обратной матрицы методом замещения
Отыскание элементов j – го столбца обратной матрицы сводится к нахождению коэффициентов разложения единичного вектора по вектор-столбцам матрицы А.
Сначала необходимо определить, является ли матрица А вырожденной или нет. Однако это можно установить в процессе нахождения обратной матрицы методом замещения.
Для определения коэффициентов разложения методом замещения составляется таблица с удвоенным количеством столбцов, состоящая из элементов матриц А и единичной матрицы Е. Слева записывается данная по условию матрица, а справа – единичная. Последовательно заменяются единичные векторы базиса вектор - столбцами матрицы А. В результате на месте исходной матрицы должна получиться единичная матрица, а справа – обратная матрица.
На каждом шаге решения выбирается разрешающий элемент аrs¹0 (любой элемент матрицы коэффициентов А, отличный от нуля), r –я строка называется направляющей (разрешающей) строкой, а s–й столбец - направляющим (разрешающим) столбцом. Элементы направляющей (разрешающей) строки делятся на разрешающий элемент, а элементы других строк заменяются на новые по правилу прямоугольника:
![]() ,
где
,
где
![]() - определяемый
элемент;
- определяемый
элемент;
![]() - заменяемый
элемент;
- заменяемый
элемент;
![]() – элементы,
стоящие в оставшихся углах прямоугольника:
– элементы,
стоящие в оставшихся углах прямоугольника:
![]() - элемент
направляющей строки,
стоящий в одном столбце с заменяемым
элементом
- элемент
направляющей строки,
стоящий в одном столбце с заменяемым
элементом
![]() ;
;
![]() -
элемент направляющего
столбца, стоящий в одной
строке с заменяемым элементом
;
-
элемент направляющего
столбца, стоящий в одной
строке с заменяемым элементом
;
аrs- направляющий элемент.
С хема
правила прямоугольника:
хема
правила прямоугольника:
После получения новой таблицы выбирается новый, отличный от нуля, разрешающий элемент в другой строке, вычисляется новая таблица и т.д., пока в результате замещения на месте исходной матрицы А появится единичная матрица Е, а на месте единичной – обратная А-1. Если в результате вычислений обратной матрицы окажется, что процесс замещения продолжить нельзя (все направляющие элементы равны нулю), то матрица является вырожденной и обратной матрицы А-1 для данной матрицы А не существует.
Рассмотрим сущность метода на примере.
Пример.
Дана матрица
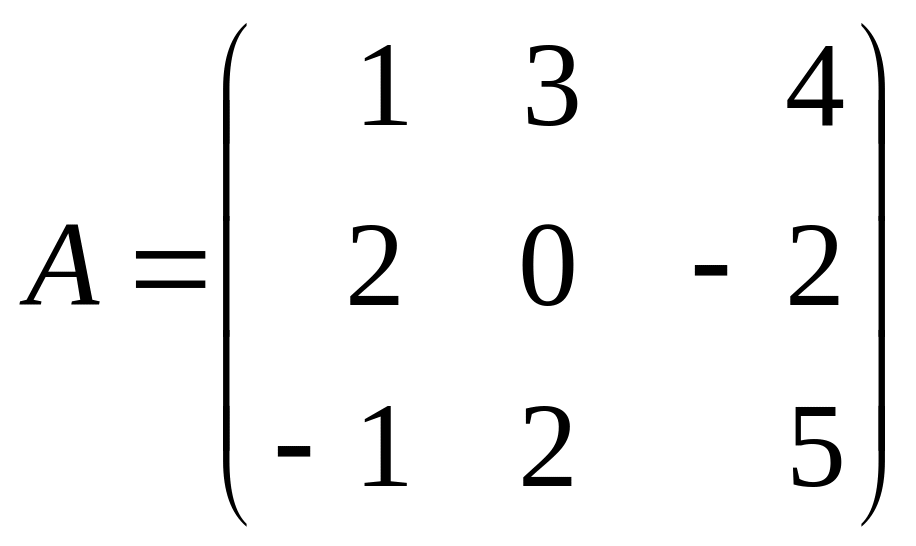 .
Требуется найти для нее обратную
А-1.
.
Требуется найти для нее обратную
А-1.
Решение.
Нахождение
обратной матрицы начинается с составления
исходной таблицы, элементами которой
являются коэффициенты разложения
векторов
![]() по векторам базиса
по векторам базиса
![]() .
.
Б |
а1 |
а2 |
а3 |
е1 |
е2 |
е3 |
е1 |
1 |
3 |
4 |
1 |
0 |
0 |
е2 |
2 |
0 |
-2 |
0 |
1 |
0 |
е3 |
-1 |
2 |
5 |
0 |
0 |
1 |
Заменим
вектор
![]() вектором
вектором
![]() .
Разрешающую переменную следует исключить
из остальных уравнений, поэтому на месте
разрешающего элемента добиваемся
единицы, разделив элементы разрешающей
строки на разрешающий элемент, а остальные
элементы направляющего столбца будут
равны нулю.
.
Разрешающую переменную следует исключить
из остальных уравнений, поэтому на месте
разрешающего элемента добиваемся
единицы, разделив элементы разрешающей
строки на разрешающий элемент, а остальные
элементы направляющего столбца будут
равны нулю.
Б |
а1 |
а2 |
а3 |
е1 |
е2 |
е3 |
а1 |
1 |
3 |
4 |
1 |
0 |
0 |
е2 |
0 |
-6 |
-10 |
-2 |
1 |
0 |
е3 |
0 |
5 |
9 |
1 |
0 |
1 |
Введем
в базис вектор
![]() вместо вектора
вместо вектора
![]() .
После вычислений получим следующую
таблицу:
.
После вычислений получим следующую
таблицу:
В Б |
а1 |
а2 |
а3 |
е1 |
е2 |
е3 |
а1 |
1 |
0 |
-1 |
0 |
|
0 |
а2 |
0 |
1 |
|
|
|
0 |
е3 |
0 |
0 |
|
|
|
1 |
Теперь
введем в базис вектор
![]() вместо вектора
вместо вектора
![]() .
В итоге получим таблицу,
.
В итоге получим таблицу,
Б |
а1 |
а2 |
а3 |
е1 |
е2 |
е3 |
а1 |
1 |
0 |
0 |
-1 |
|
|
а2 |
0 |
1 |
0 |
2 |
|
|
а3 |
0 |
0 |
1 |
-1 |
|
|
в которой на месте исходной матрицы стоит единичная матрица, а на месте единичной - обратная:
 .
.
Убедимся в правильности решения:




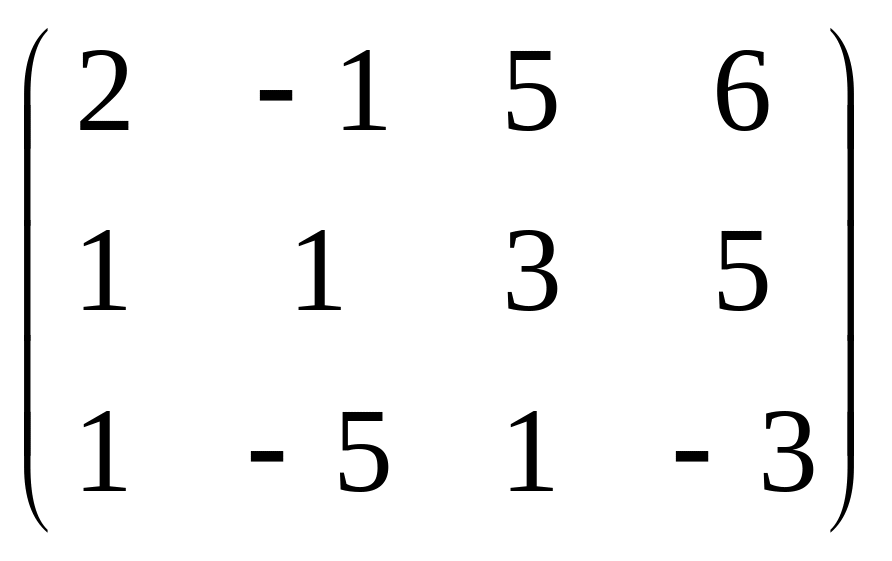
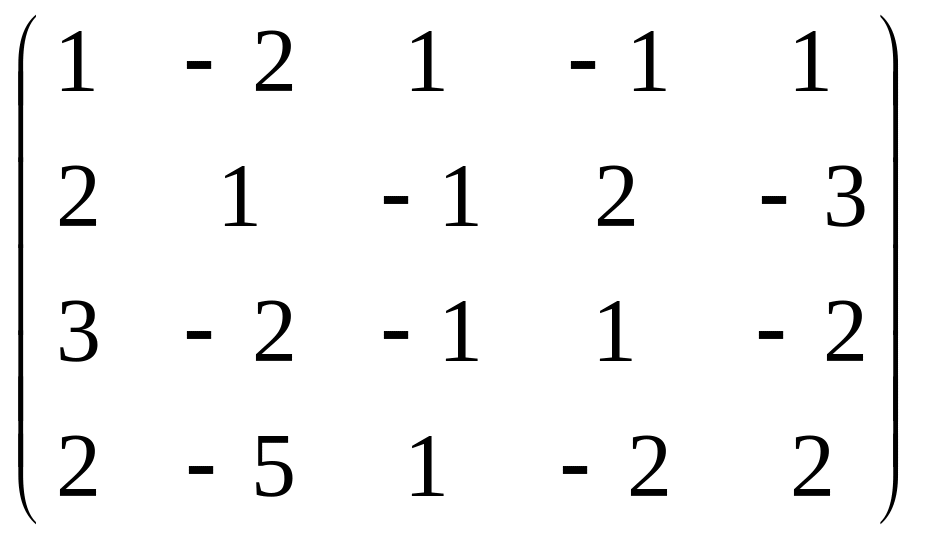
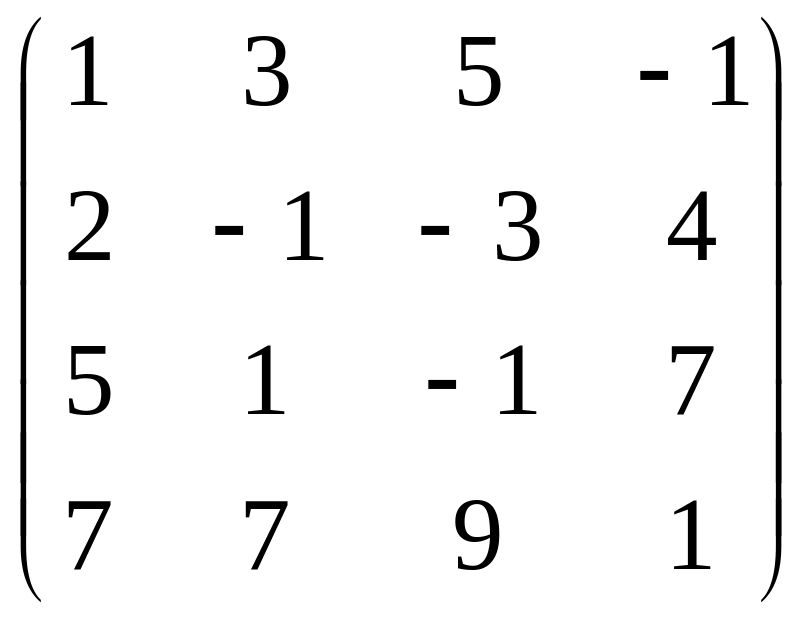


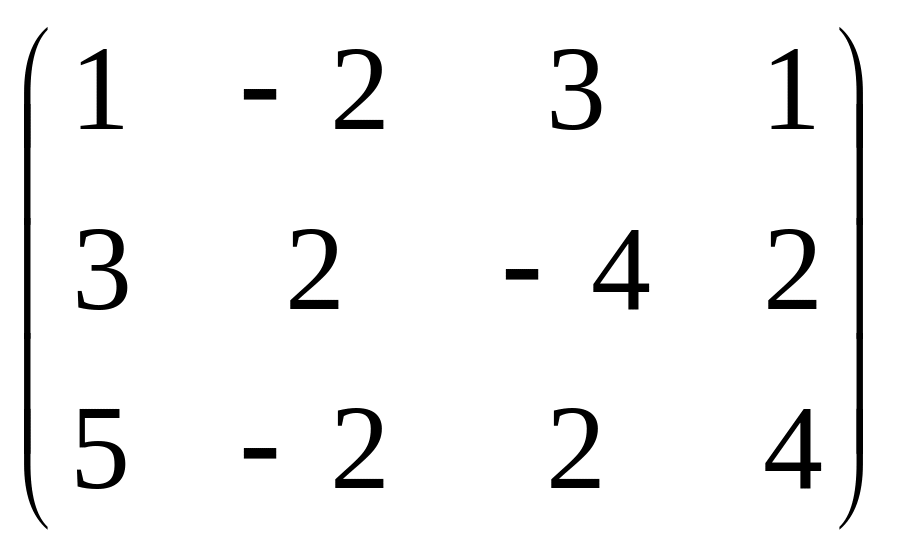
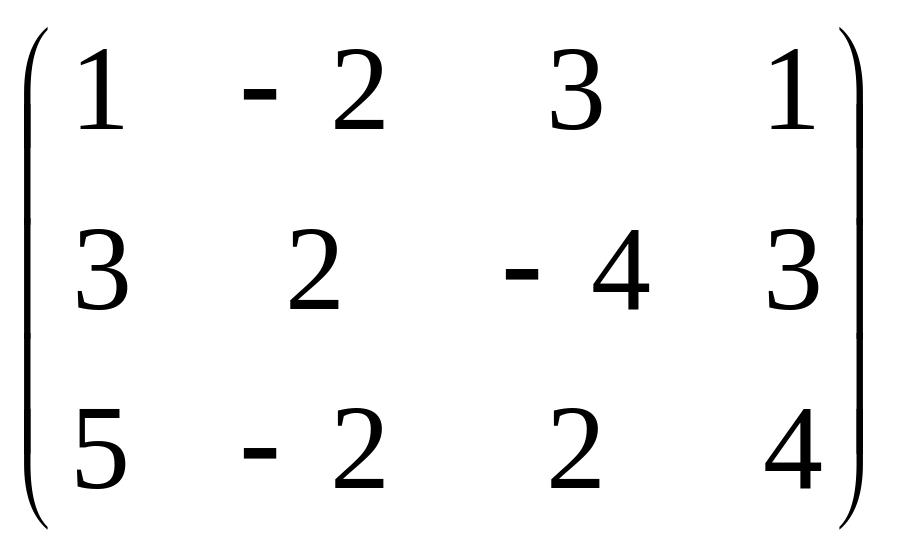

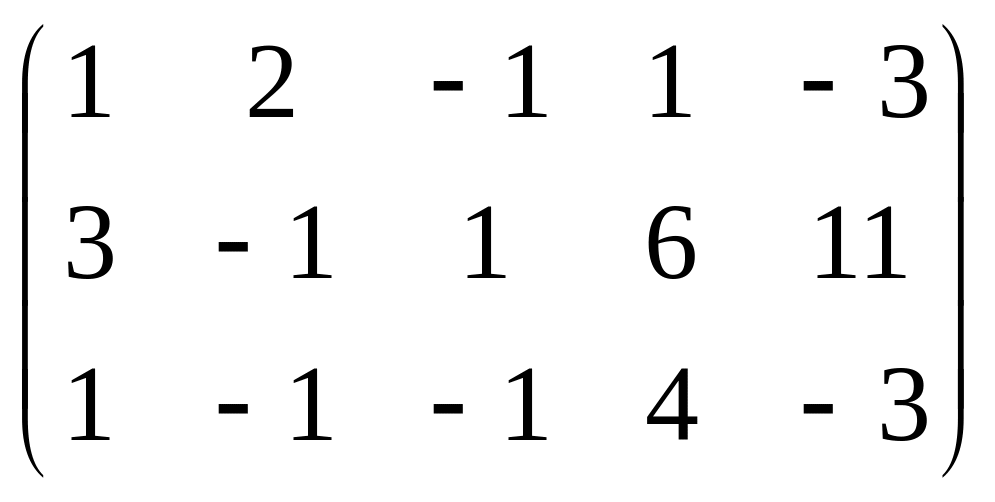
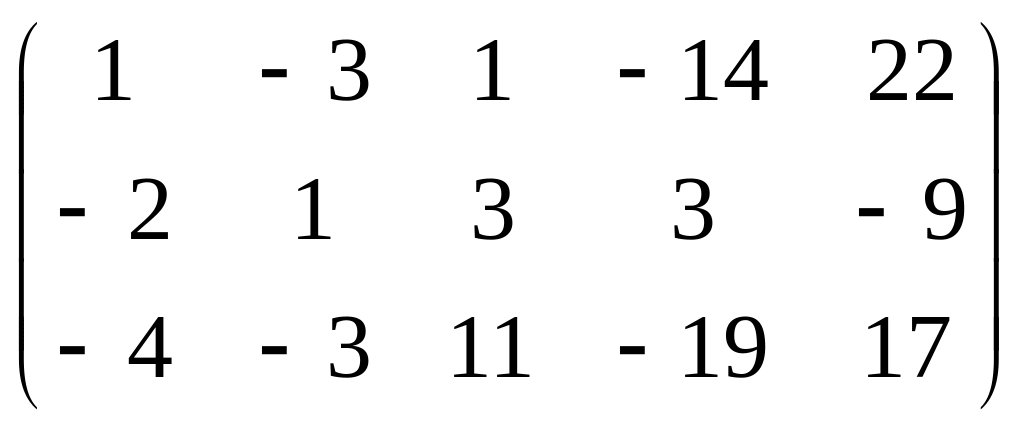

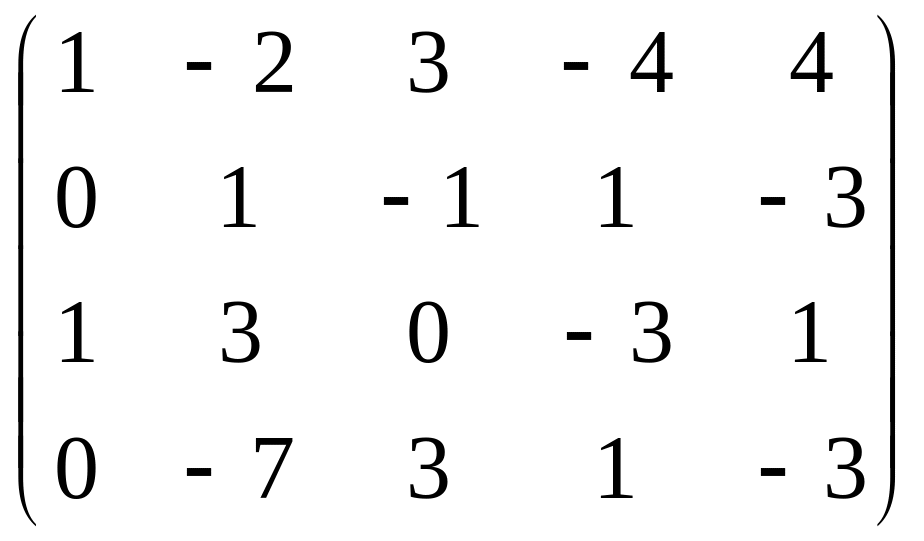
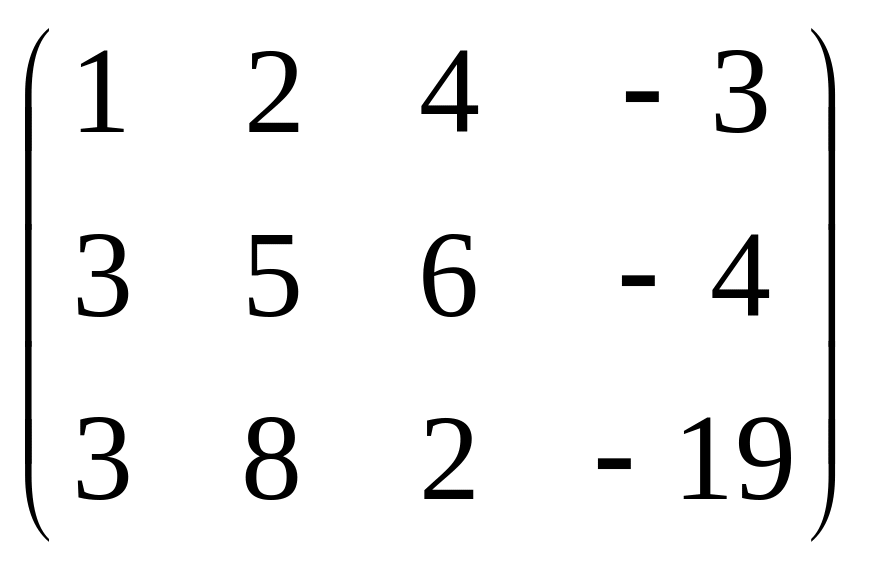

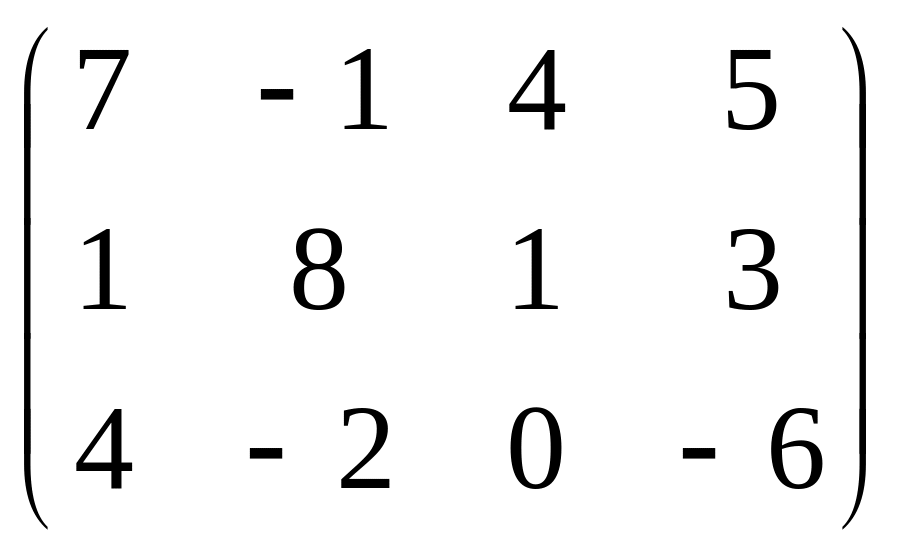
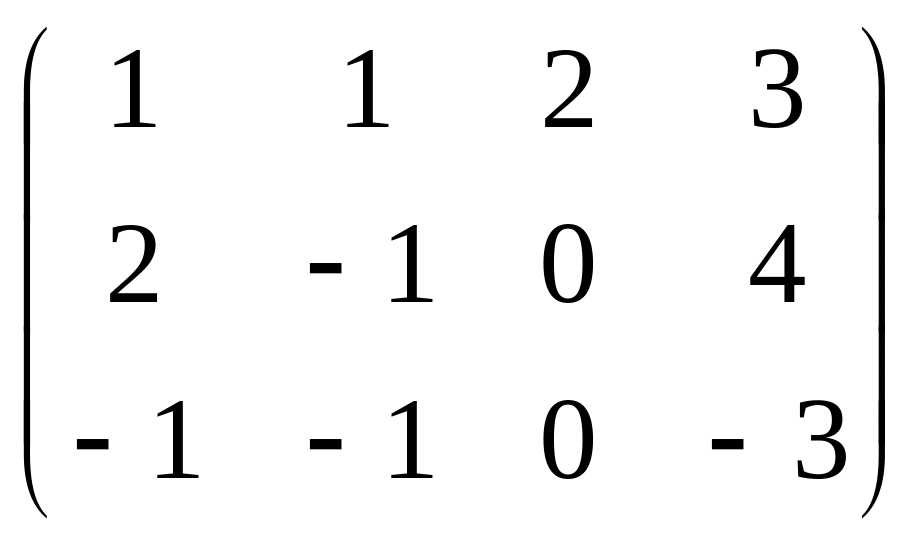

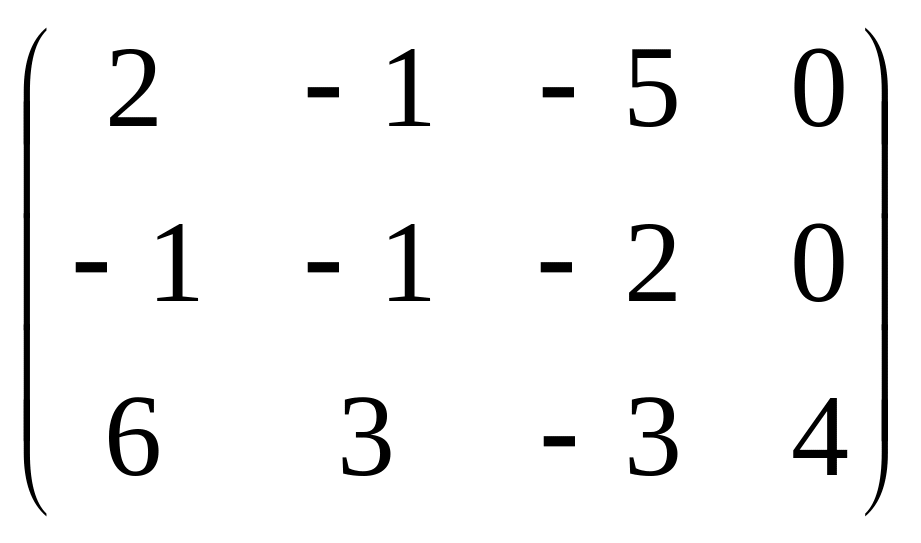


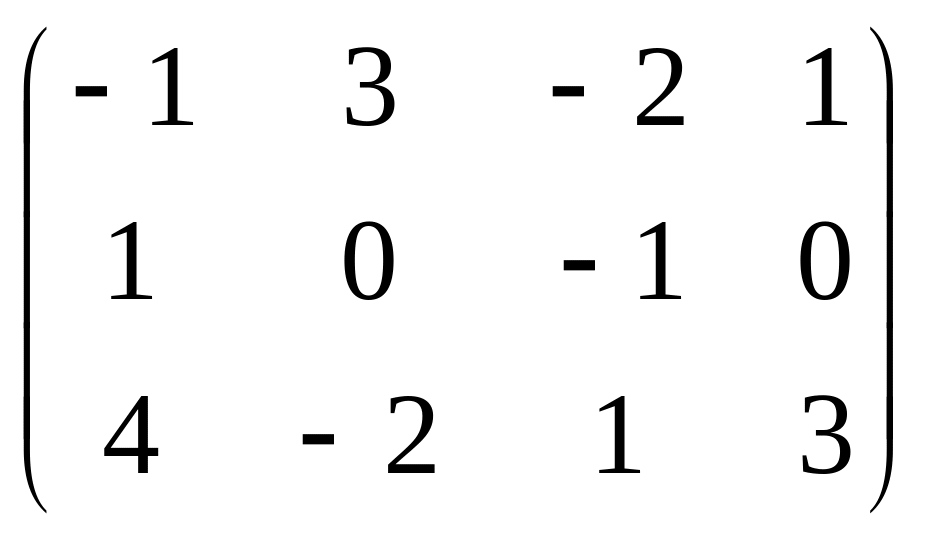

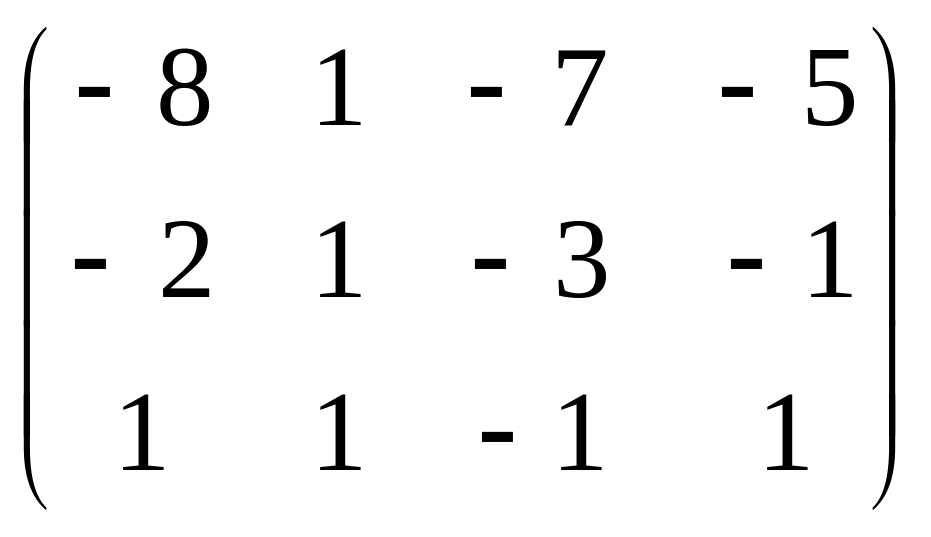
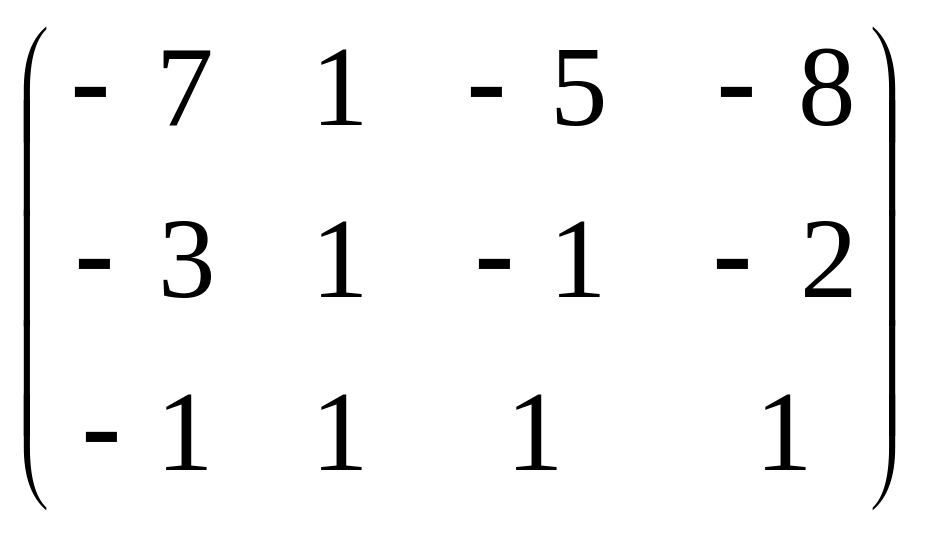

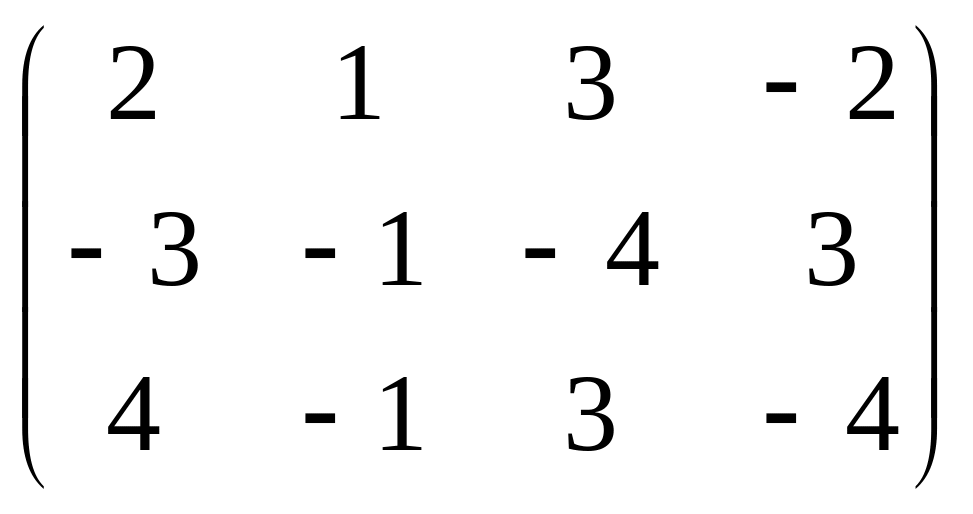


 В
В В
В В
В