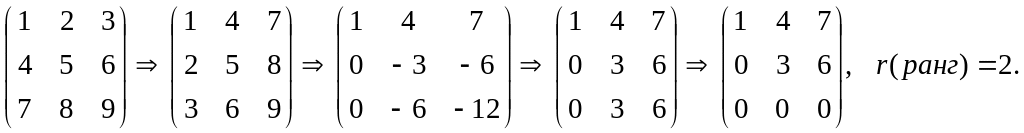- •Оглавление
- •Введение
- •Тема 1. N-мерное векторное пространство
- •Тема 2. Матрицы и определители
- •Тема 3. Системы линейных уравнений
- •Тема 4. Системы однородных линейных уравнений
- •Тема 5. Системы линейных неравенств
- •1.1 Векторы и действия над ними
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •1.2 Линейная зависимость векторов
- •1.2.1 Ранг и базис системы векторов
- •1.2.2 Переход от одного базиса к другому Метод замещения
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •1.3 Разложение вектора по базису
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •2. Матрицы и определители
- •2.1 Основные сведения о матрицах
- •2.1.1 Операции над матрицами
- •Умножение матрицы на число.
- •Сложение матриц.
- •Вычитание матриц.
- •Умножение матриц.
- •Возведение в степень матриц.
- •Транспонирование матриц.
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •2.2 Определители (детерминанты) квадратных матриц
- •2.2.1 Основные методы вычисления определителей
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •2.3 Ранг матрицы
- •1. Метод окаймляющих миноров.
- •Метод элементарных преобразований.
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •2.4 Обратная матрица
- •Нахождение обратной матрицы методом замещения
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •3. Системы линейных уравнений
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •4. Системы линейных однородных уравнений
- •Упражнения
- •Контрольные задания
- •Типовой расчет
- •5. Линейные неравенства
- •Упражнения
- •Контрольные задания
- •Вопросы для теоретического опроса
- •Список рекомендуемой литературы Основная литература
- •Дополнительная литература
- •Математика Линейная алгебра Методические указания и задания для самостоятельной работы студентов всех специальностей
- •410052, Саратов, ул. Международная, 24
- •410052, Саратов, ул. Международная, 24
1. Метод окаймляющих миноров.
Алгоритм метода окаймляющих миноров
Найти какой-нибудь минор первого порядка М1 (т.е. элемент матрицы), отличный от нуля. Если такого минора нет, то матрица нулевая и ранг матрицы равен нулю.
Вычислить миноры второго порядка, содержащие М1 (окаймляющие М1) до тех пор, пока не найдется минор М2, отличный от нуля. Если такого минора нет, то ранг матрицы
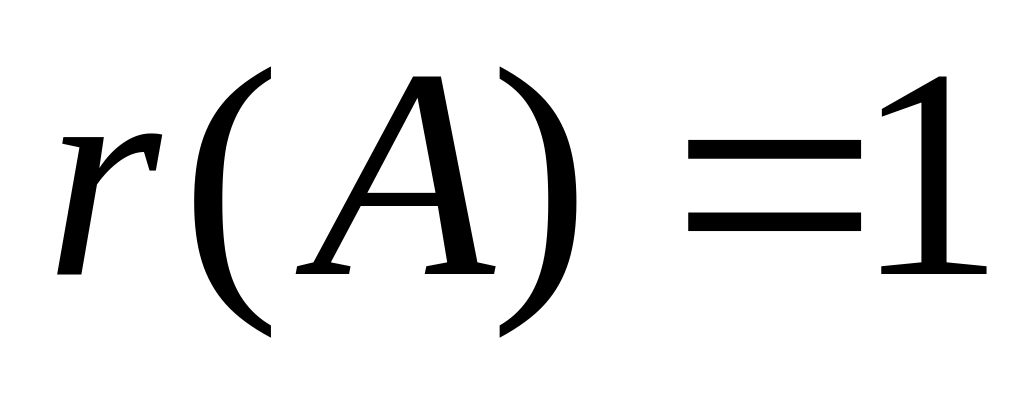 ,
если есть, то
,
если есть, то
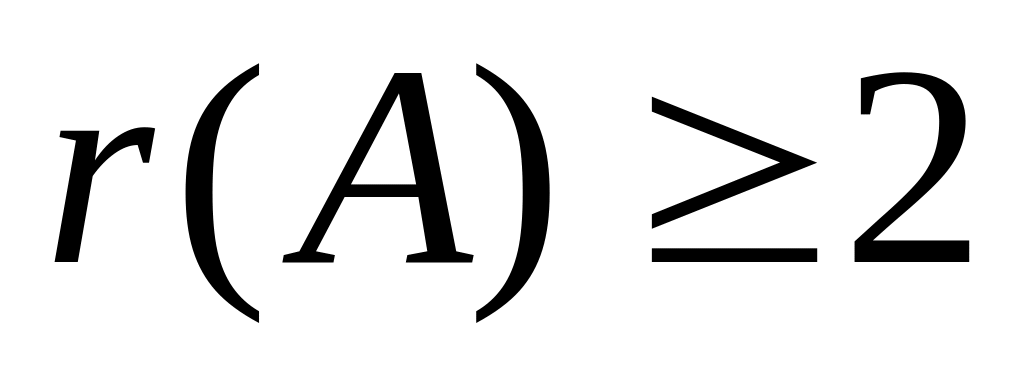 и т.д.
и т.д.Вычислить (если они существуют) миноры k- го порядка, окаймляющие минор Мk-1, отличный от нуля. Если такого минора нет, то ранг матрицы
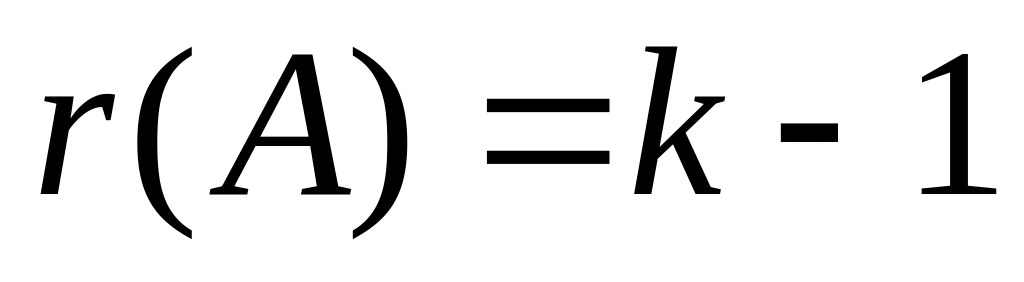 ,
если есть, то
,
если есть, то
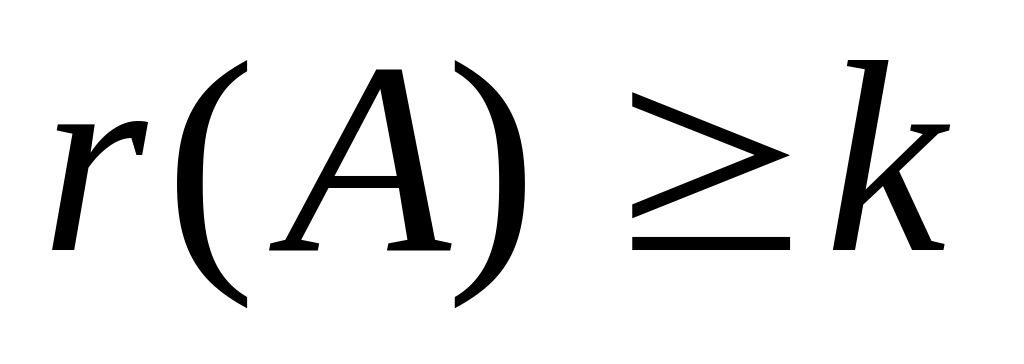 и т.д.
и т.д.
При нахождении ранга матрицы таким способом достаточно на каждом шаге найти всего один ненулевой минор k- го порядка, причем его ищут его среди миноров, содержащих минор Мk-1, отличный от нуля.
Пример. Найти ранг матрицы методом окаймляющих миноров:
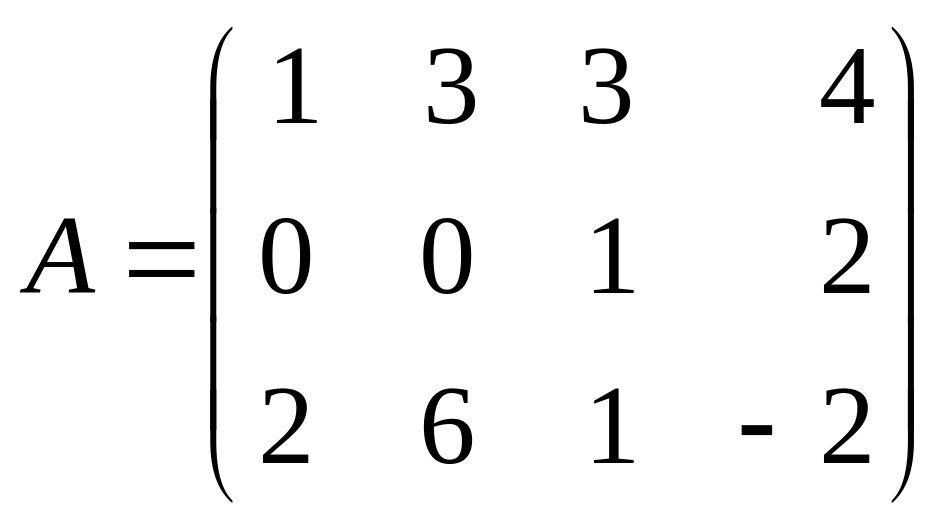 .
.
Решение. Так как
у матрицы А есть ненулевые элементы,
то ранг матрицы r(A)≥1. Найдем
какой-нибудь минор второго порядка.
Таким минором является, например,
![]() .
Значит, r(A)≥2.
.
Значит, r(A)≥2.
Вычислим миноры третьего порядка, окаймляющие минор М2.
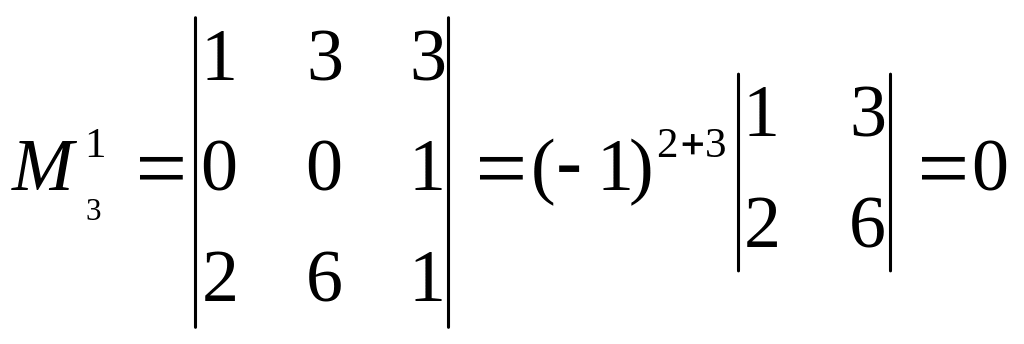 ;
; 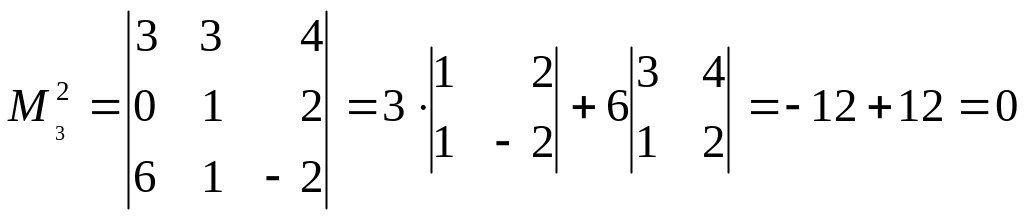 .
.
Все миноры третьего порядка, окаймляющие минор М2, равны нулю, следовательно, r(A)<3, т.е. r(A)=2.
Метод элементарных преобразований.
С помощью элементарных преобразований можно привести матрицу к так называемому ступенчатому виду, когда вычисление ранга не составляет труда.
Алгоритм метода элементарных преобразований
Если элемент матрицы
![]() ,
перестановкой строк и столбцов добиваются
того, что бы
,
перестановкой строк и столбцов добиваются
того, что бы
![]() .
.
Если , то умножая элементы первой строки на подходящие числа и затем складывая их с соответствующими элементами других строк, добьемся того, чтобы все элементы первого столбца, кроме , равнялись нулю. Аналогично проводят преобразования для остальных строк.
Если в процессе преобразований получаются строки (или столбцы), полностью состоящие из нулей, то отбрасываем эти строки (или столбцы). При этом получаем матрицу ступенчатого вида.
Таким образом, ранг ступенчатой матрицы равен количеству ее ненулевых строк (или числу ненулевых элементов главной диагонали матрицы ступенчатого вида).
Пример. Найти
ранг матрицы:
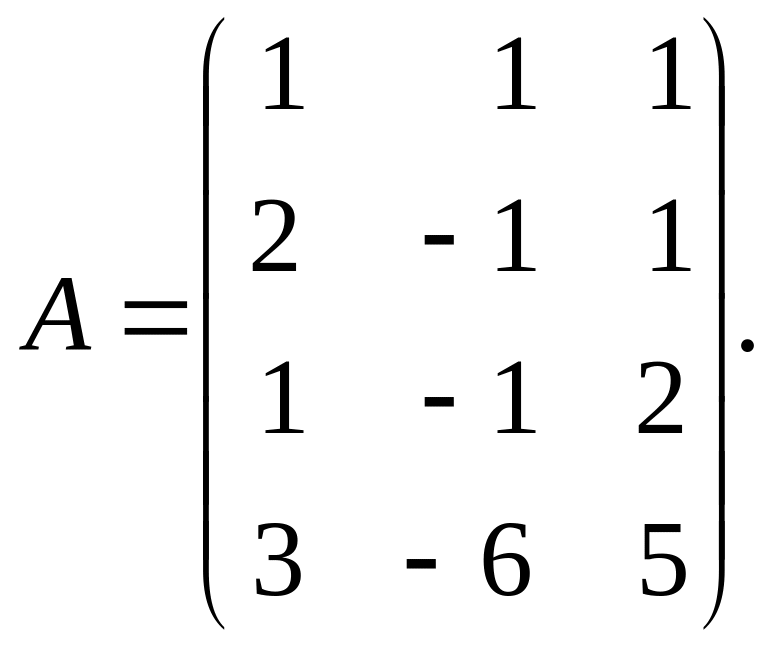
Решение. Матрица А имеет размер 4×3, значит, r(A)≤3. С помощью элементарных преобразований, не меняющих ранг матрицы, приведем матрицу А к ступенчатому виду.
Транспонируем матрицу А.
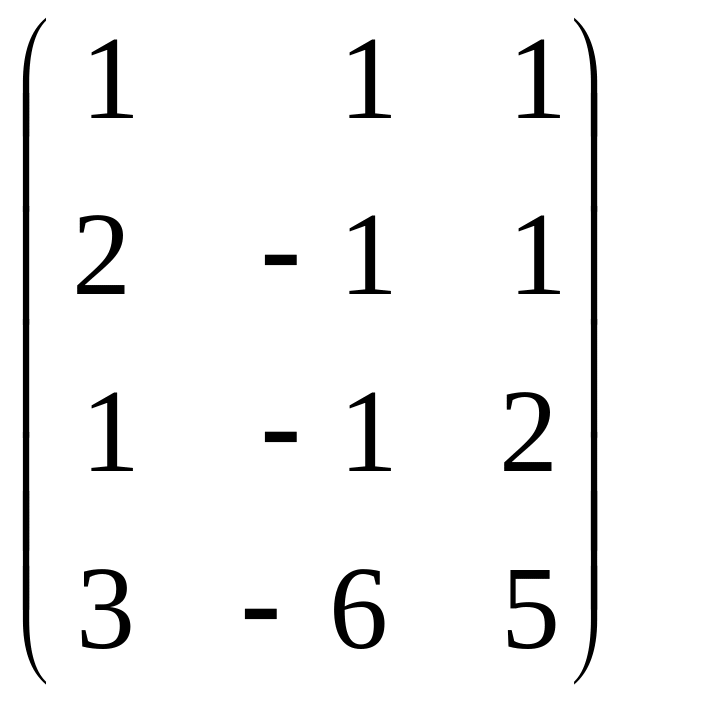 ~
~
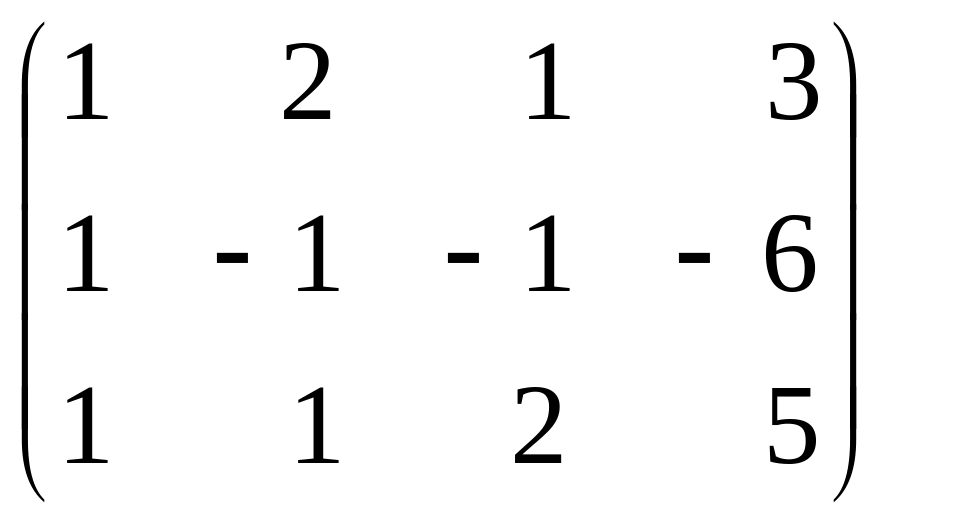
(-1)
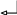
 ~
~
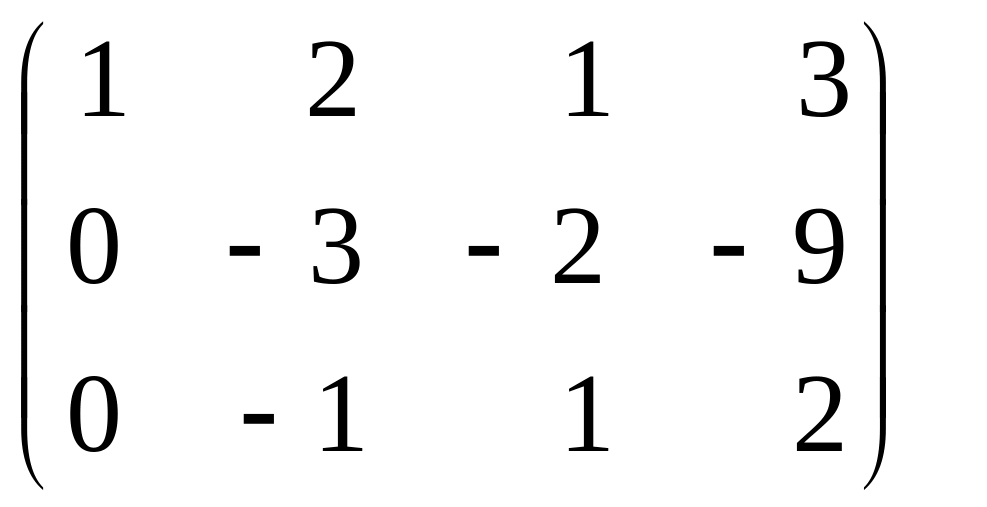
В новой матрице поменяем местами вторую и третью строки. Затем сделаем нулевыми все элементы матрицы под крайним элементом второй строки для чего умножим элементы второй строки на (-3) и сложим ее с третьей строкой матрицы:
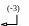
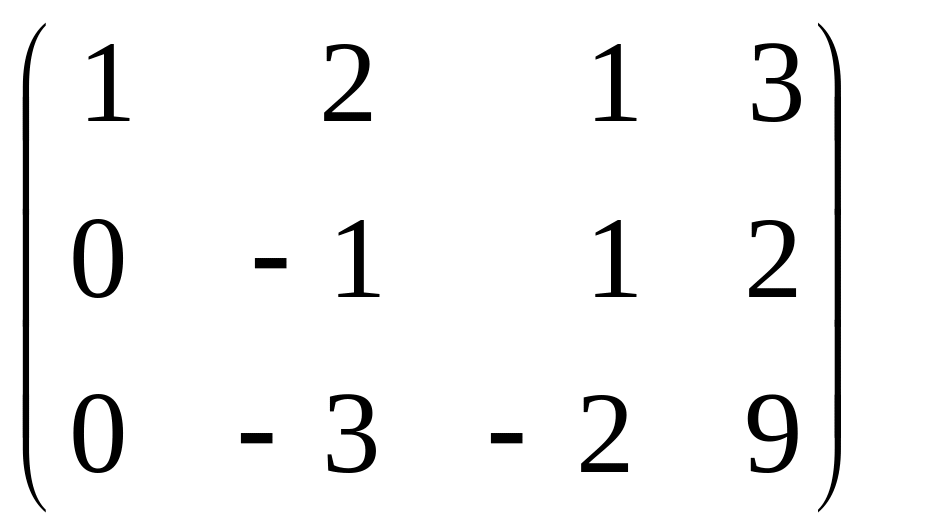 ~
~
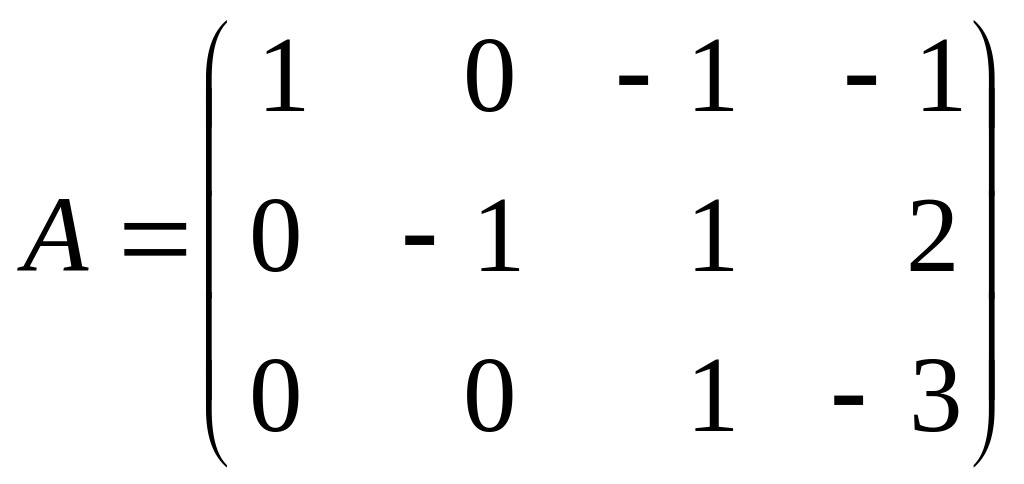 .
.
Получили ступенчатую матрицу размера 3×4, у которой три ненулевых элемента на главной диагонали. Таким образом, эта матрица имеет ненулевой минор 3-го порядка, например,
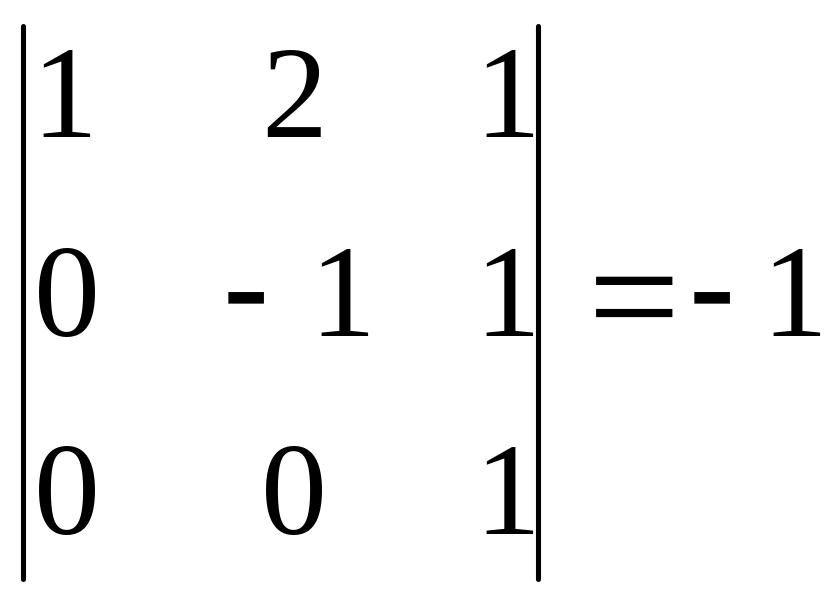 .
.
Значит, r(A)=3.
Понятие ранга тесно связано с понятием линейной зависимости и независимости ее строк или столбцов.
Строки
матрицы А
![]() (
(![]() )
называются линейно
зависимыми,
если существуют такие числа
)
называются линейно
зависимыми,
если существуют такие числа
![]() ,
одновременно не равные нулю, что линейная
комбинация строк матрицы равна нулевой
строке:
,
одновременно не равные нулю, что линейная
комбинация строк матрицы равна нулевой
строке:
![]() .
.
В противном случае строки матрицы называются линейно независимыми.
Линейная зависимость матрицы означает, что хотя бы одна строка матрицы является линейной комбинацией остальных.
Теорема. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки (столбцы).
Например:
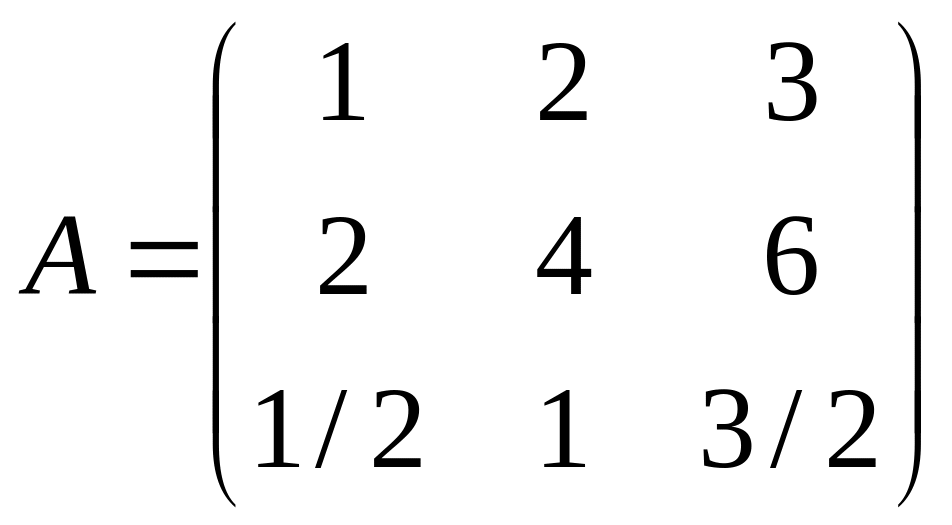 ,
n =
3, r
= 1,
,
n =
3, r
= 1,
то есть порядок матрицы равен 3, а ранг равен 1, так как линейно независимой является только первая строка. Вторая и третья строки получаются умножением первой строки на соответствующий коэффициент (в данном случае — это коэффициенты 2 и ½).
Квадратная матрица называется невырожденной (неособенной), если порядок матрицы совпадает с рангом матрицы.
При вычислении ранга матрицы производят те же преобразования, что и при вычислении определителя.
Пример. Найти
ранг матрицы