2. Представление экспертной информации в виде

систем нечетких высказываний.

Обозначим через X,Y,Z,..., например, множество значений входных параметров процесса проектирования, которые существенно влияют на выбор выходного параметра V.

Введем лингвистические переменные <β_x, T_x, X, G_x, M_x>, <β_y, T_y, Y, G_y, M_y>, …, <β_v, T_v, V, G_v, M_v>, определенные на множествах X,Y,Z,...,V.

Системы эталонных логических высказываний, отражающие опыт эксперта в типовых ситуациях, представим в виде :

(10.9)

или в виде :

(10.10)

где m - число базовых значений лингвистической переменной ;

- высказывания вида:

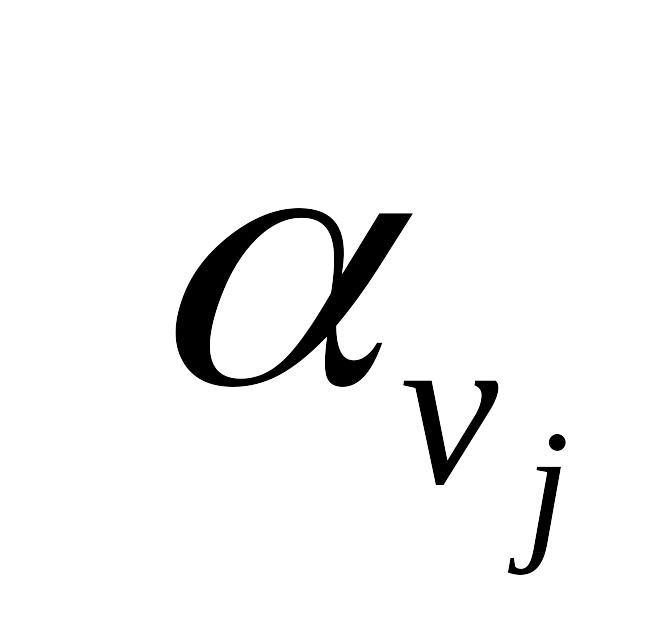
Высказывание Е_ji представляет собой i- тую входную эталонную нечеткую ситуацию , которая может иметь место, если лингвистическая переменная примет значение . Значения - являются нечеткими переменными с функциями принадлежности:

Системы нечетких высказываний (10.9) и (10.10) также как и ранее рассмотренные четкие системы отражают два разных случая взаимосвязи входных и выходных параметров проектирования.

В первом случае в зависимости от значений входных параметров делается вывод об эталонных значениях выходного параметра. Во втором случае в зависимости от возможных значений выходного параметра делается предположение о возможных значениях входных параметров.

С помощью правил преобразования лингвистических выражений (правило 13) системы (10.9),(10.10) можно представить более компактно.

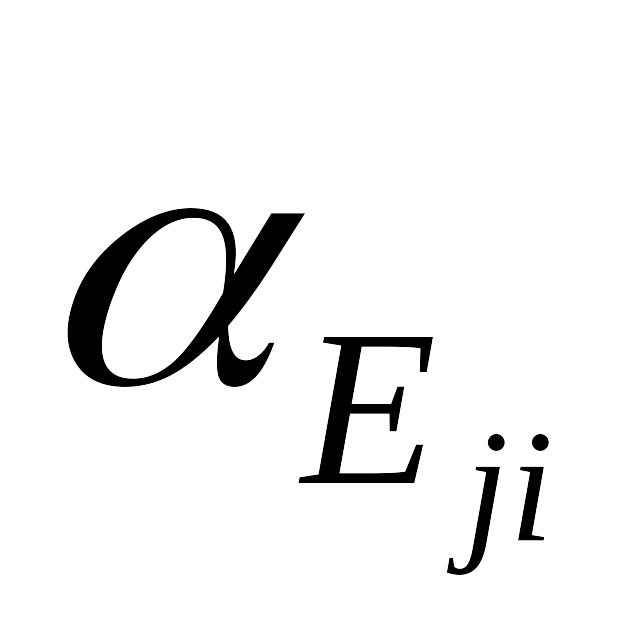Согласно правилу 1 высказывание можно представить в виде , где - лингвистическая переменная, определенная на множестве и принимающая базовые значения с функциями принадлежности

Согласно правилу 2 высказывания и в (10.19) и (10.10) можно представить в виде :

где - значение лингвистической переменной с функцией принадлежности

(10.11)

Обозначив через A_j и В_j высказывания можем записать (10.1) и (10.2) в виде:

(10.12)

(10.13)

Систему эталонных нечетких логических высказываний вида (10.12) называют нечеткой системой первого типа, а систему (10.13) - системой второго типа.

Рассмотрим ряд определений, необходимых для анализа нечеткой информации.

БАЗОВЫЕ ЗНАЧЕНИЯ T_w лингвистической переменной , соответствующие высказываниям Е_ij, назовем ВХОДНЫМИ НЕЧЕТКИМИ ЭТАЛОННЫМИ СИТУАЦИЯМИ , а БАЗОВЫЕ ЗНАЧЕНИЯ Т_v лингвистической переменной - ВЫХОДНЫМИ НЕЧЕТКИМИ ЭТАЛОННЫМИ СИТУАЦИЯМИ .

Системы нечетких экспертных высказываний представимы в виде соответствия. Так система L⁽¹⁾ - типа может задаваться соответствием вида F⁽¹⁾ = (T_w, T_v, F₁) 4. T_w - область отправления (множество входных эталонных ситуаций ); T_v - область прибытия (или выходных эталонных ситуаций ); F₁ С T_w x T_v - график соответствия.

Аналогично система высказываний L⁽²⁾ - типа задается соответствием F⁽²⁾ = (T_w, T_v, F₂), где F₂ C T_v x T_w.

Графики соответствия представляются в виде двудольного ориентированного графа. В левой части графа вершинам соответствуют области отправления, а в правой - области прибытия.

Например:

Рис. 10.1. Графы соответствий.

- значения входной лингвистической переменной нечетких систем высказываний переменной (эталонные входные ситуации);

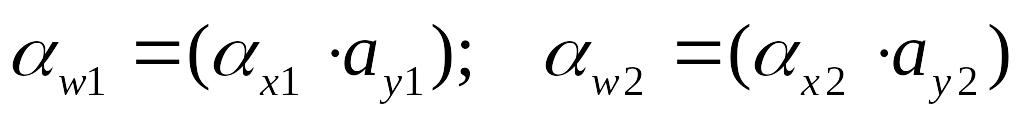
Система нечетких высказываний называется ЛИНГВИСТИЧЕСКИ ПОЛНОЙ, если выполняется условие (для нечеткой системы первого типа):

и для нечеткой системы второго типа:

В противном случае система является ЛИНГВИСТИЧЕСКИ ВЫРОЛЖДЕННОЙ. Двудольный граф соответствия для синтаксически невырожденной системы первого (второго) типа в правой (левой) части не содержит изолированных вершин.

Невырожденные системы Вырожденные системы

1тип 2 тип 1 тип 2 тип

Рис.10.2.

Система нечетких высказываний называется ЛИНГВИСТИЧЕСКИ НЕИЗБЫТОЧНОЙ, если выполняется условие

Это условие означает, что двудольный граф соответствия, определяющего систему высказываний, не содержит повторяющихся пар вершин.

Система нечетких высказываний называется ЛИНГВИСТИЧЕСКИ НЕПРОТИВОРЕЧИВОЙ, если выполняется условие

В двудольном графе соответствия лингвистически непротиворечивой системы первого (второго) типа из каждой вершины левой части (в каждую вершину правой части) графа выходит (входит) не более одного ребра (рис.10.2)

Обозначим через истинность высказывания относительно . НЕПРОТИВОРЕЧИВОСТЬЮ нечеткой системы L называют величину Т_L, определяемую выражением: