Лекция 9 продукционные модели представления знаний

План лекции

1. Модули, управляемые образцами

2. Типы и структура правил-продукций

3.Классификация ядер продукций

4.Методы поиска решений в продукционных системах

5. Методы логического вывода

6. Стратегии выбора правил при логическом выводе

1. МОДУЛИ, УПРАВЛЯЕМЫЕ ОБРАЗЦАМИ

В традиционном программировании команды устанавливаются в жесткой фиксированной последовательности. По умолчанию после выполнения i-й команды выполняется (i+1)-я команда, если i-я команда не является командой ветвления. Все места ветвления в традиционном программировании указываются явно. Подобный способ программирования удобен в тех случаях, когда последовательность обработки мало зависит от обрабатываемых данных, т.е. тогда, когда ветвление является исключением, а не нормой. В противном случае программу лучше рассматривать как совокупность независимых модулей, управляемых образцами. На каждом шаге работы такая программа анализирует текущую ситуацию и определяет по анализу образцов, какой модуль подходит для обработки этой ситуации.

Каждый управляемый образцом модуль (УОМ) состоит из механизмов исследования и модификации одной или нескольких структур данных. Диапазон УОМ может колебаться в широких пределах от простого продукционного правила до процедуры произвольной степени сложности, вызываемой по образцу. Каждый УОМ на очередном шаге работы анализирует данные рабочей памяти, проверяя наличие структур, которые сопоставляются с его образцом. Системы, построенные на основе управляемых образцами модулей, называют системами вывода, управляемыми образцами [Хэйес-Рот и др., 1978]. Функции управления в этих системах осуществляет интерпретатор.

С точки зрения представления знаний подход, использующий управляемые образцами модули, можно охарактеризовать следующими особенностями:

1. Разделение постоянных знаний, хранимых в базе знаний, и временных знаний, хранимых в рабочей памяти.

2. Структурная независимость модулей. Это свойство облегчает модификацию и совершенствование системы, что чрезвычайно важно для экспертных систем, постоянно модифицирующих свои знания. Кроме того, независимость модулей упрощает объединение программ, написанных разными авторами.

3. Отделение схемы управления от модулей, несущих знания о проблемной области. Данное свойство позволяет применять различные схемы управления.

Системы вывода, управляемые образцами, имеют весьма различное исполнение. Примерами УОМ являются и конкурирующие акторы [Хьюитт, 1973], и источники знаний [Эрман и др. 1980, 1981], и фреймы [Минский, 1975], и даже вершины в сетях Петри [Петри, 1962; Котов, 1984; Зисман 1978].

Системы, управляемые образцами, классифицируются в соответствии с ограничениями, накладываемыми на модули. На рис. 1 приведена классификация систем, управляемых образцами, которая может рассматриваться и как классификация модулей, управляемых образцами.

Если системы, управляемые образцами, состоят из модулей, локализованных на вершинах сети, которые активизируются сигналами, приходящими по дугам, то такие системы называют системами, основанными на сетях .

Большинство систем, управляемых образцами, удовлетворяет следующему ограничению: все исследования данных рабочей памяти в каждом модуле объединены и предшествуют всем действиям по модификации данных. Таким образом, модуль разделяется на две части: предусловие, исследующее данные, и действие, модифицирующее данные. Модули,

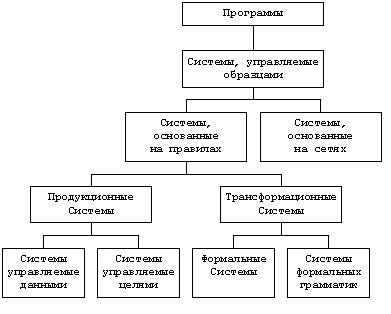
Рис.1. Классификация систем, управляемых образцами

имеющие такое деление, называют правилами [Хэйес-Рот и др., 1978], а системы, использующие такие правила, называют системами, основанными на правилах (см. рис. 1). Попутно отметим, что разделение операции исследования и модификации данных облегчает отладку системы.

Системы, основанные на правилах, разделяются по видам правил на продукционные системы и трансформационные системы. Продукционные системы образованы из правил, в которых сопоставление и планирование (управление) являются явными функциями системы, зафиксированными в интерпретаторе. Трансформационные системы, в отличие от продукционных, могут не иметь явных функций по сопоставлению правил и управлению правилами. Примерами трансформационных систем являются формальные системы и системы формальных грамматик.

2. ТИПЫ И СТРУКТУРА ПРАВИЛ-ПРОДУКЦИЙ

Продукции наряду с фреймами являются наиболее популярными средствами представления знаний в ЭС. Продукции, с одной стороны, близки к логическим моделям, что позволяет организовывать на них эффективные процедуры вывода, а с другой стороны, более наглядно отражают знания, чем классические логические модели. В них отсутствуют жесткие ограничения, характерные для логических исчислений, что дает возможность изменять интерпретацию элементов продукции. В общем виде под продукцией понимаегся выражение следующего вида:

(i); Q; Р; А=>В, N.

Здесь i—имя продукции, с помощью которого данная продукция выделяется из всего множества продукций. В качестве имени может выступать некоторая лексема, отражающая суть данной продукции (например, «покупка книги» или «набор кода замка»), или порядковый номер продукции в их множестве, хранящемся в .памяти системы.

Элемент Q характеризует сферу применения продукции. Такие сферы легко выделяются в когнитивных структурах человека. Наши знания как бы «разложены по полочкам». На одной «полочке» хранятся знания о том, как надо готовить пищу, на другой—как добраться до работы и т. п. Разделение знаний на отдельные сферы позволяет экономить время на поиск лужных знаний. Такое же разделение на сферы в базе знаний ИС целесообразно и при использовании для представления знаний продукционных моделей.

Основным элементом продукции является ее ядро: А=>В. Интерпретация ядра продукции может быть различной и зависит oi того, что стоит слева и справа от знака секвенции =>. Обычное прочтение ядра продукции выглядит так: ЕСЛИ А, ТО В, более сложные конструкции ядра допускают в правой части альтернативный выбор, например, ЕСЛИ А, ТО B1, ИНАЧЕ B2, Секвенция может истолковываться в обычном логическом смысле как знак логического следования В из истинного А (если А не является истинным выражением, то о В ничего сказать нельзя). Возможны и другие интерпретации ядра продукции, например А описывает некоторое условие, необходимое для того, чтобы можно было совершить действие В.

Элемент Р есть условие применимости ядра продукции. Обычно Р представляет собой логическое выражение (как правило, предикат). Когда Р принимает значение «истина», ядро продукции активизируется. Если Р ложно, то ядро продукции не может быть использовано. Например, если в продукции «НАЛИЧИЕ ДЕНЕГ; ЕСЛИ ХОЧЕШЬ КУПИТЬ ВЕЩЬ X, ТО ЗАПЛАТИ В КАССУ ЕЕ СТОИМОСТЬ И ОТДАЙ ЧЕК ПРОДАВЦУ» условие применимости ядра продукции ложно, т. е. денег нет, то применить ядро продукции невозможно.

Элемент N описывает постусловия продукции Они актуализируются только в том случае, если ядро продукции реализовалось. Постусловия продукции описывают действия и процедуры, которые необходимо выполнить после реализации В. Например, после покупки некоторой вещи в магазине необходимо в описи товаров, имеющихся в этом магазине, уменьшить количество вещей такого типа на единицу. Выполнение N может происходить »ие сразу после реализации ядра продукции.