Вимірювання та обробка результатів.

1. Зібрати електричне коло згідно рис. 4.5.

2. Компенсувати струм через мікроамперметр шляхом підбору напруги. Для цього включити освітлювач і за допомогою потенціометра підібрати таке значення напруги U_з, при якому не тече струм через гальванометр. Вимірювання провести окремо для п’ятьох світлофільтрів.

3. Результати занести у табл. 4.1.

Таблиця 4.1. Результати вимірів

Довжина хвилі світлофільтрів λ, нм	, Гц	Uз, В	h, Дж⋅с	A, eB
Червоний, 687
Оранжевий, 656
Жовтий, 589
Синій, 431
Фіолетовий, 400

4. Побудувати графік .

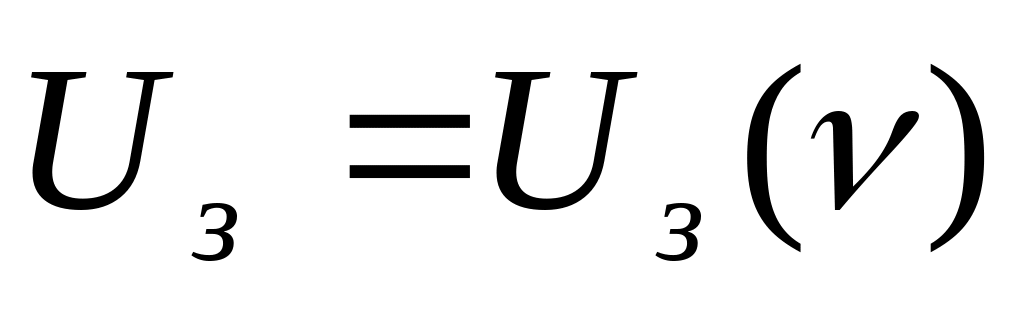5. За значенням тангенса кута нахилу прямої знайти величину 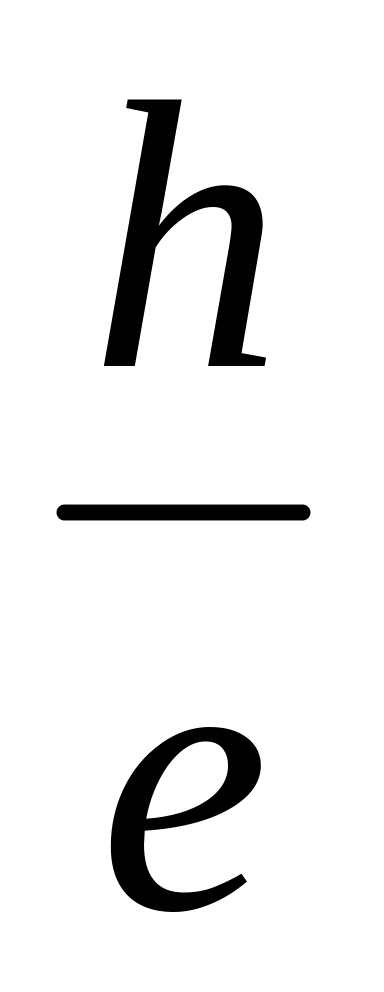, після чого визначити сталу Планка.

6. За величиною відрізку, що відсікає функція 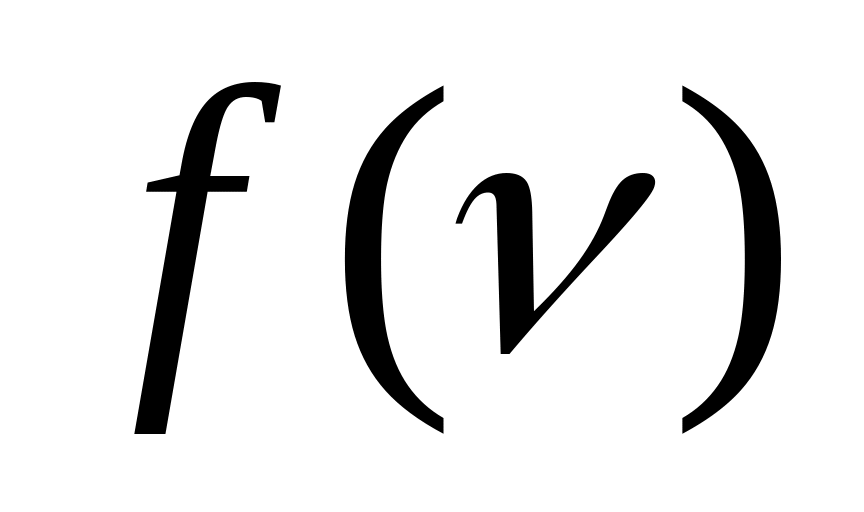на осі ОY, визначити роботу виходу електронів.

7. Одержані значення для h i A порівняти з табличними. Знайти похибки розрахунків за результатами вимірів.

Контрольні питання.

1. Що називається фотоефектом? Які види фотоефекту Вам відомі ? Що в них спільного і чим вони відрізняються?

2. Сформулювати закони зовнішнього фотоефекту.

3. Які властивості фотоефекту неможливо пояснити з точки зору хвильової природи світла?

4. Записати формулу Ейнштейна і розкрити її фізичний зміст.

5. Що називається червоною границею фотоефекту і від чого залежить її значення?

6. Розрахувати червону границю фотоефекту для сурм’яно-цезієвого катоду. Як зміниться ця величина у випадку багатофотонних процесів?

7. Чому в якості фотоелемента зручніше використовувати сферичний конденсатор, а не плоский?

8. Як зміниться ток насичення, якщо замість вакуумного фотоелемента використовувати газонаповнений?

9. Розповісти про метод визначення h i A у даній роботі.

10. Яким чином по показниках вольтметра можна визначити контактну різницю потенціалів між анодом і катодом?

11. Доказати, що поглинання фотона вільним електроном є несумісним з законами збереження енергії та імпульсу. Яким чином можна пояснити, що явище фотоефекту не протирічить доказаному твердженню?

Лабораторна робота № 5

СПІВВІДНОШЕННЯ НЕВИЗНАЧЕНОСТЕЙ ДЛЯ ФОТОНІВ

Прилади і обладнання: джерело світла (гелій - неоновий лазер ЛГН -109), оптична скам’я, щілина із змінною шириною, екран, лінійка.

Теоретичні відомості.

Принцип невизначеностей Гейзенберга для координати та імпульсу частинки. У класичній механіці стан матеріальної точки в кожний момент часу характеризується її положенням і імпульсом. Реальні мікрочастинки-електрони, протони, атоми та інші - більш складні об'єкти. Не можна характеризувати миттєвий стан мікрочастинки точними завданнями її положення й імпульсу. Причина цього полягає в тому, що будь-яка мікрочастинка виявляє і корпускулярні і хвильові властивості. Не можна сказати, що у певній точці простору довжина хвилі дорівнює , оскільки довжина хвилі є характеристика синусоїди, а це є періодична крива.

З іншого боку, якщо будь-яке хвильове утворення займає обмежену область простору, то його завжди можна представити синусоїдами. Тільки однієї синусоїди для цього недостатньо. Потрібен хвильовий пакет - суперпозиція безлічі синусоїд різних частот, що підсилювалися б у певному інтервалі простору ∆х і взаємно гасили би один одного поза цим інтервалом. Якщо довжина хвильового пакета ∆х, то хвильові числа k, необхідні для його утворення, не можуть займати який завгодно вузький інтервал. Мінімальна ширина інтервалу повинна задовольняти умові:

. (5.1)

Це абсолютно хвильове співвідношення.

Виражаючи через , співвідношення (5.1) можна переписати у вигляді:

. (5.2)

Це співвідношення називається співвідношенням чи принципом невизначеностей Гейзенберга для координати й імпульсу частинки.

Але його не можна тлумачити таким чином, що частинка в кожен момент часу має певні значення х і р, але ми їх не можемо визначити з більшою точністю, ніж це дозволяє співвідношення невизначеностей. Зміст співвідношення (5.2) відбиває той факт, що в природі об'єктивно не існує стану частинок з точно визначеними значеннями х і р.

Співвідношення (5.2) проявляється при всякій спробі виміру точного положення чи точного імпульсу частинки. Виявляється, що уточнення положення частинки позначається на збільшенні неточності в значенні імпульсу, і навпаки. Перевірці цього співвідношення і присвячується дана робота.

Співвідношення невизначеностей для фотонів. Нехай рух фотона описується плоскою монохроматичною хвилею де Бройля . Фотон у такому стані має цілком визначений імпульс:

, (5.3)

але його координата зовсім не визначена. Для визначення x- координати фотона на шляху поширення хвилі ставиться непрозорий екран із щілиною ширини . Якщо фотон пройшов через щілину, то в площині самої щілини координата x буде зафіксована з точністю ~a. Однак після проходження щілини в результаті дифракції хвильова функція фотона зміниться. Вона буде мати максимуми і мінімуми (рис. 5.1). Фотон може бути виявлений у будь-якому місці, де 0. 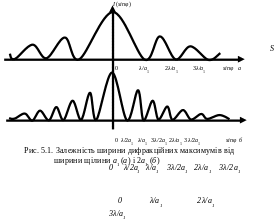Як видно з рис. 5.1, практично усе хвильове поле буде зосереджено в межах центрального максимуму. Його кутова ширина дорівнює 2 (рис. 5.2), а умова максимуму відповідно має вигляд:

. (5.4)

Враховуючи, що випромінювання розповсюджується як на кути більше , так і на кути менше , можна записати наступну хвильову умову невизначеності, якій підкоряються кути для більшої частини плоских хвиль, розсіяних на щілині:

. (5.4 а)

З формули (5.4а) випливає, що звуження щілини (а) обов'язково супроводжується розширенням сектору напрямку (sin ), в якому зосереджено дифракційне поле. Як видно з рис. (5.1), при збільшенні ширини щілини вдвічі, тобто при а₂=2а₁, інтервал значень sin φ, що відповідає центральному максимуму, скорочується вдвічі.

Після проходження через щілину у фотона з'являється x-компонента імпульсу (рис. 5.2):

. (5.5)

Для фотонів, що відхиляються на різні кути, як менше φ, так і більше φ, значення Р_x різні. В цьому випадку вираз (5.4а) з урахуванням (5.5) запишеться у вигляді:

чи , (5.6)

• де 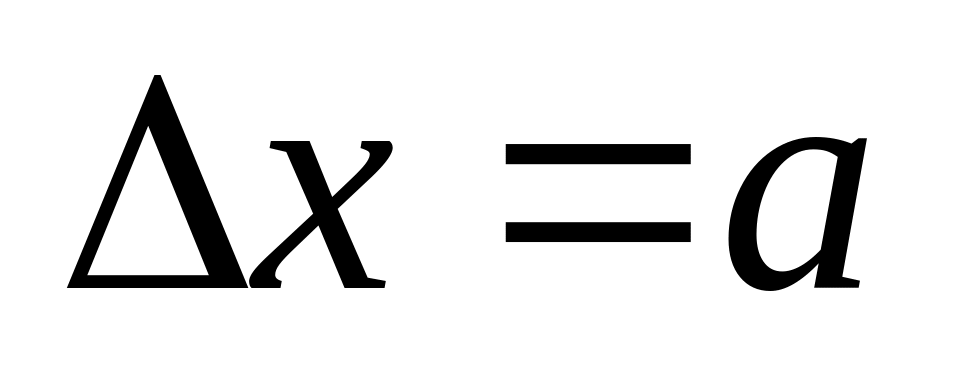- область локалізації (невизначеність

місцеположення) фотонів в площині екрану;

- область значень (невизначеність) компонент

імпульсу.

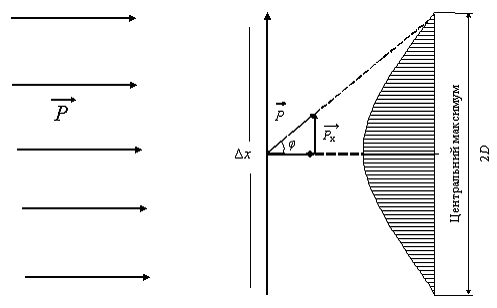
Рис. 5.2. Схема проходження фотонів через щілину

Співвідношення (5.6) показує, що добуток невизначеності координати на невизначеність відповідного їй імпульсу має величину порядку h= 6,62·10^-34 Дж∙с. Чим точніше визначена одна з цих величин, наприклад чим вужче щілина, через яку проходять фотони, тим невизначеніший стає імпульс Р_х, і, навпаки, чим ширше щілина (х), тим більш визначений імпульс (Р_х0). Очевидно, якщо одна з величин має цілком певне значення, то інша є абсолютно невизначеною.

Перевіримо співвідношення невизначеностей (5.6) за допомогою експерименту. Для цього будемо вимірювати ширину щілини, яка характеризує невизначеність координати фотона, і ширину дифракційної картини, яка характеризує невизначеність поперечної координати імпульсу фотона Р_x.

Вимірювання та обробка результатів.

Установка для перевірки принципу невизначеностей складається з джерела монохроматичного випромінювання (гелій-неоновий лазер), регульованої щілини та екрану, на якому спостерігається дифракційна картина.

1. За допомогою санчат, на яких встановлена щілина, необхідно домогтися того, щоб промінь лазера пройшов через її отвір і потрапив на екран. Змінюючи розмір (ширину) щілини х від 0,05 до 0,45 мм через кожні 0,05 мм, за допомогою лінійки і міліметрового паперу зробити 8-10 вимірювань ширини (2D) головного максимуму дифракційної картини, отриманої на екрані (див. рис. 5.2). Для збільшення точності вимірювань щілину необхідно встановити на відстані не менш 1 м від екрану. Ширину максимуму можна визначити по положенню дифракційних смуг, що огинають максимум.

2. Результати вимірювань ширини щілини х та половини ширини головного максимуму D занести до таблиці.

3. Побудувати графік залежності півширини головного максимуму D від ширини щілини х, пам’ятаючи, що х є невизначеність місцеположення фотонів у площині екрану, а D характеризує невизначеність їхнього імпульсу.

4. Розрахувати компоненту імпульсу фотона Р_х за допомогою формули (5.5). При цьому значення довжини хвилі λ прийняти як середнє значення для видимого світла (λ=633нм), а sinφ знайти з геометричного трикутника установки (tg φ 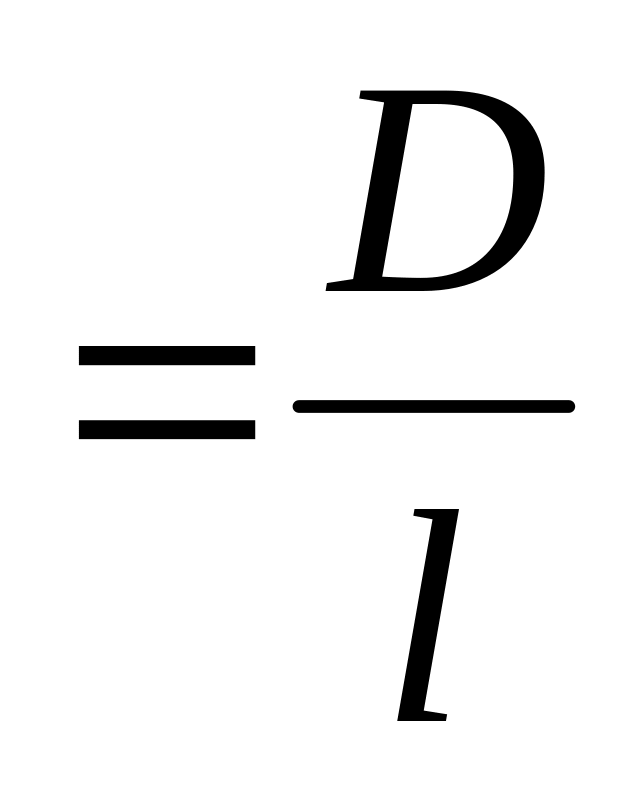, де l- відстань від щілини до екрану (див. рис. 5.2)).

5. Розрахувати невизначеність компоненти імпульсу Р_х за допомогою формули (5.6).

6. Порівняти значення Р_х та Р_х, зробити висновок щодо експериментального підтвердження співвідношення невизначеностей, використовуючи природнє припущення, що невизначеність (помилка при оцінці, похибка) деякої величини не може перебільшувати значення самої величини.