Методи визначення експериментальних похибок.

За характером походження всі похибки можна розділити на три типи:

1. Грубі похибки або промахи, пов’язані з неуважністю експериментатора під час запису відліку (наприклад, зі шкали тощо).

2. Систематичні похибки, зумовлені зсувом вимірюваного значення відносно дійсного (наприклад, збитий нуль в приладах).

3. Випадкові похибки, які проявляються в розкиданні відліків під час повторних вимірів, проведених в однакових умовах.

Виміри можуть бути:

1. прямі (фізична величина вимірюється безпосередньо зі шкали приладу) і побічні (фізична величина розраховується за формулами через інші величини, знайдені прямими вимірами);

2. однократні (одноразові) і багатократні (багаторазові).

В залежності від типів вимірів існує ряд методів визначення абсолютних і відносних похибок.

Визначення похибок під час прямих однократних вимірів:

1. за абсолютну похибку приймають значення, яке дорівнює половині поділки шкали (наприклад для звичайної лінійки );

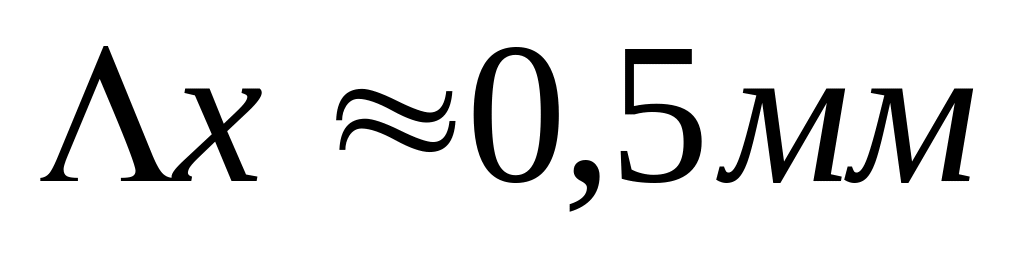2. Якщо похибки мають відоме походження, то їх характеризують класом точності приладу.

Важливою характеристикою точності приладу є приведена похибка :

, (1)

- де - абсолютна похибка;

- граничне максимальне значення на шкалі приладу.

Клас точності приладів може дорівнювати: 0,1; 0,2; 0,5 ; 1; 1,5; 2,5; 4.

Наприклад, нехай для міліамперметра клас точності становить ; мА; вимір дав результат I=50,0 мА. Абсолютну похибку знайдемо із (1):

мА.

Кінцевий запис: мА.

Визначення похибки експериментальних результатів із зазначеною довірчою ймовірністю під час багатократних прямих вимірів ( метод Ст’юдента).

1. Довірливим інтервалом називається такий інтервал , в який попадає дійсне значення вимірюваної величини із заданою ймовірністю.

2. Ймовірність того, що дійсне значення вимірюваної величини знаходиться в середині цього інтервалу , називається довірчою ймовірністю або надійністю Р.

3. Для нескінченно великої кількості вимірів 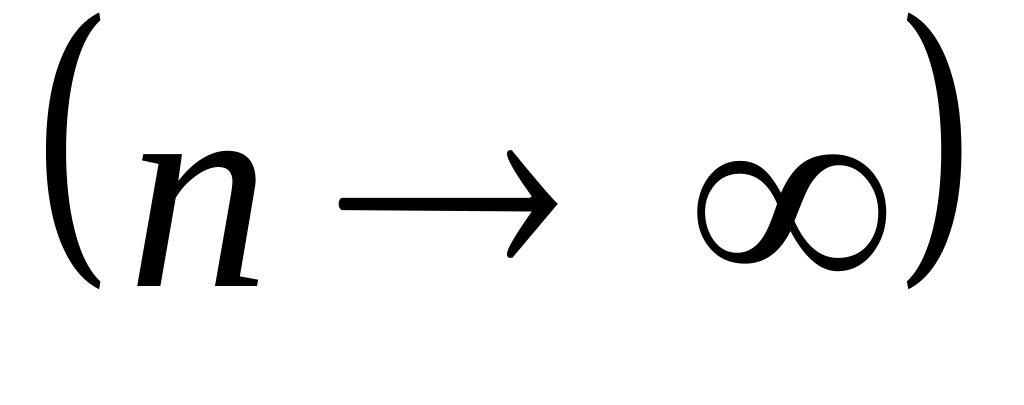розглядаються такі величини:

середня квадратична похибка окремого виміру :

;

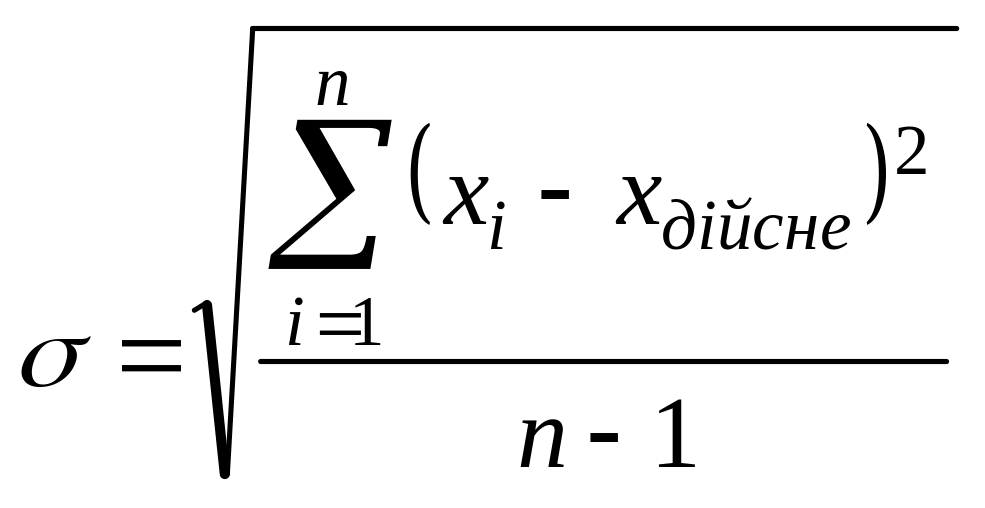середня квадратична похибка середньоарифметичного ряду вибірок :

,

- де - дійсне значення вимірюваної величини.

4. В реальних умовах для обмеженої кількості вимірів

розглядаються такі величини:

середня квадратична похибка окремого виміру:

;

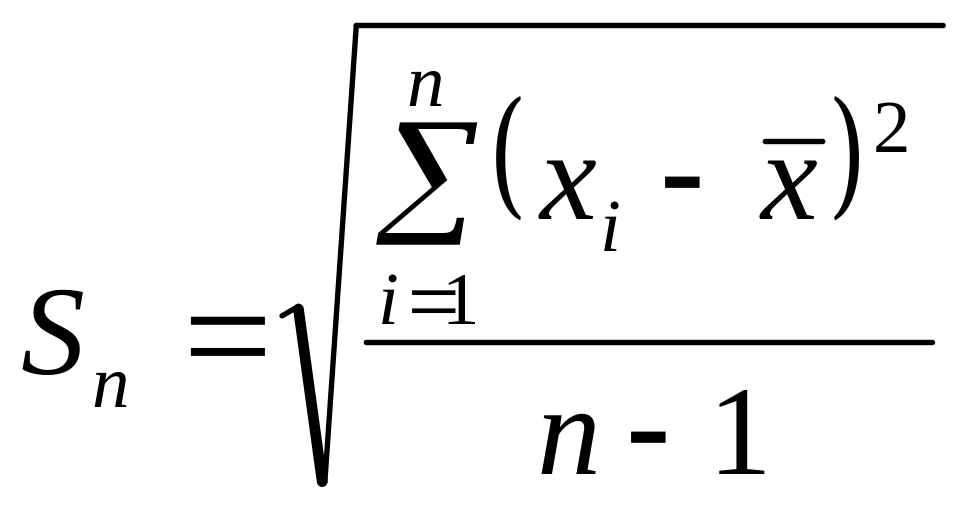середня квадратична похибка середньоарифметичного:

.

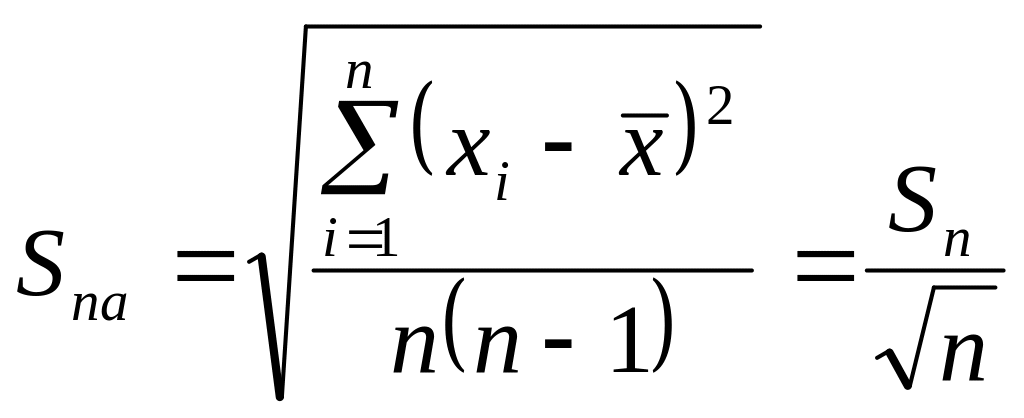- де - середнє значення вимірюваної величини.

Англійський математик В.С. Госсет (псевдонім Ст’юдент) на підставі теорії ймовірності запропонував визначати довірливий інтервал (абсолютну похибку) формулою:

,

-де - середня квадратична похибка середньо-

арифметичного;

- коефіцієнт Ст’юдента, який знаходиться із таблиці

для заданої довірчої ймовірності (надійності) Р

і числа вимірів n.

Порядок операцій визначення похибок методом Ст’юдента.

1. Всі виміри записують в таблицю.

2. Підраховують середнє значення :

.

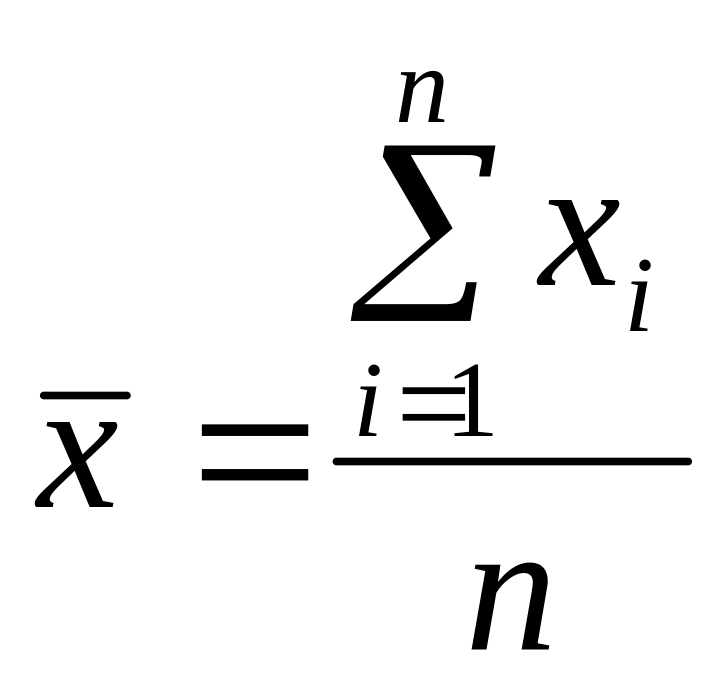3. Знаходять абсолютні похибки кожного виміру:

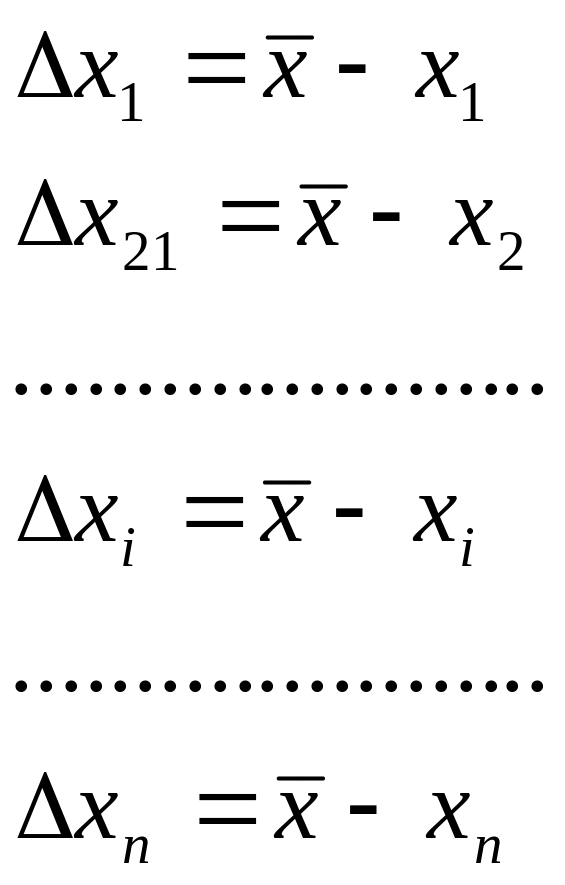
4. Визначають середньоквадратичну похибку середньо-

арифметичного:

.

5. Задають значення надійності Р (довірливої ймовірності), наприклад, Р=0,7.

6. За таблицею, яка додається, знаходять коефіцієнт Ст’юдента t

за відомими Р і n (число вимірів).

5. Знаходять довірливий інтервал , тобто абсолютну похибку :

.

5. Визначають відносну похибку результату вимірів:

.

9. Кінцевий результат записують у вигляді:

.

_.

Визначення похибок під час непрямих (побічних вимірів )

фізичної величини методом диференціювання.

Відомо, що під час побічних вимірів потрібна величина знаходиться за результатами прямих вимірів інших фізичних величин, які зв’язані із нею функціональною залежністю (формулою).

В цьому випадку необхідно визначити абсолютні похибки всіх вимірюваних величин. З метою виведення формули для розрахунку похибки користуються правилами диференціювання.

1. Нехай фізична величина залежить від однієї перемінної: . Тоді . Змінюючи диференціали на кінцеві різниці, отримаємо правило для знаходження похибок:

.

2. Фізична величина залежить від декількох перемінних:

. Тоді . Виконуючи заміну диференціалів (нескінченно малі прирости аргументів) на кінцеві різниці, одержимо:

.

В останньому рівнянні всі додатки беруться позитивними.

Розглянемо ряд прикладів.

1)

.

2)

3)

4)

5)

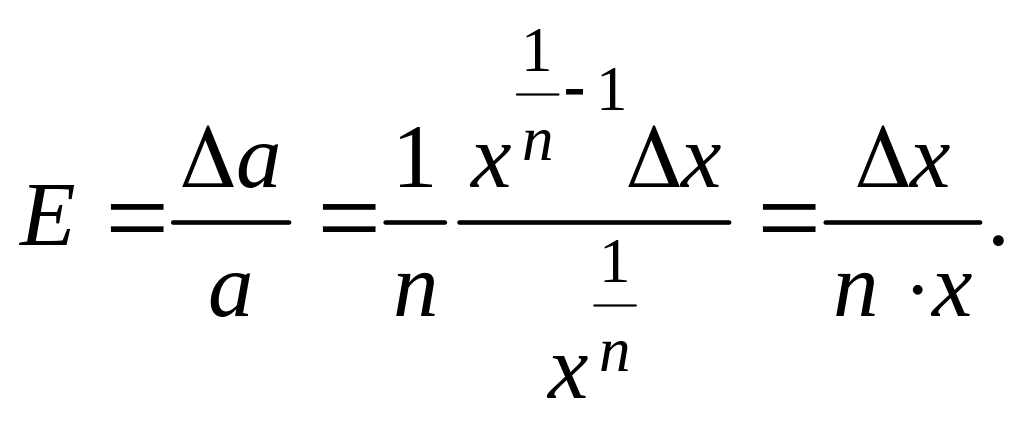
6)

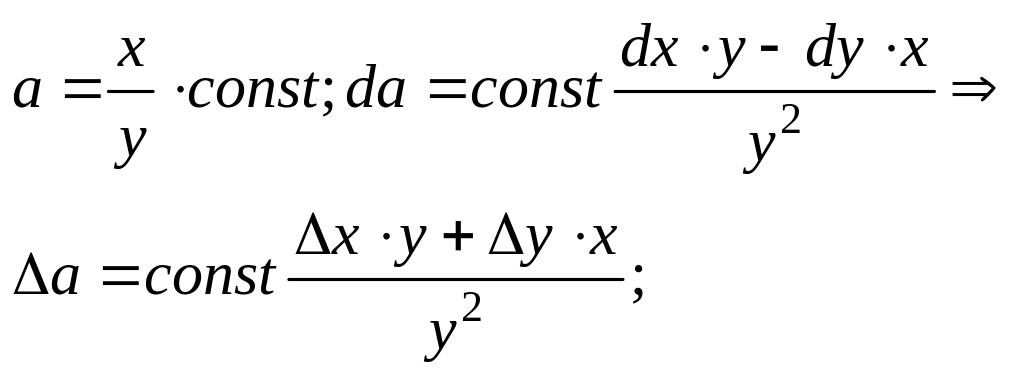
7)

8)

9)

10)

Приклад визначення похибок під час непрямих (побічних) вимірів фізичної величини методом диференціювання.

У одній з лабораторних робіт з механіки коефіцієнт в’язкості визначається за формулою:

, (1)

- де - густини падаючої кульки і рідини;

- діаметр кульки;

- час падіння кульки;

- пройдений шлях кульки;

- прискорення вільного падіння.

Позначимо чисельник через , а знаменник – через :

, (2)

• де (добуток трьох множників),

Згідно попередніх формул з виразу (2) отримаємо:

(3)

Аналогічно запишемо :

(4)

. (5)

Після підстановки (4) і (5) в (3) маємо:

. (6)

Підрахувавши за формулою (6) відносну похибку, можна знайти абсолютну похибку :

.

Кінцевий результат записуємо у вигляді:

.

Визначення похибок під час непрямих (побічних) вимірів фізичної величини методом логарифмування.

Спочатку вираз логарифмується, а потім диференціюється, за допомогою табличного співвідношення

.

Наприклад, густина речовини товстостінної труби дорівнює:

,

• де і - зовнішній і внутрішній діаметри відповідно,

- висота труби.

Логарифмуємо попередній вираз:

.

Після диференціювання маємо:

.

Замінюючи диференціали на кінцеві різниці і знак ’’-’’ на ’’+” (з метою визначення максимальної похибки), останнє рівняння перепишеться у вигляді:

.

Величини та - відомі, тому після підрахування відносної похибки можна знайти абсолютну похибку:

.

Кінцевий результат записуємо у вигляді:

.