Интерполяционный многочлен в форме Лагранжа

В основе нахождения интерполяционных многочленов в форме Лагранжа лежит построение вспомогательных многочленов . В общем виде интерполяционный многочлен Лагранжа степени имеет вид где .

В частности,

;

;

Заметим, что наименьшая степень многочлена, удовлетворяющая условию интерполирования для таблицы из узлов, равна , а наибольшую степень такого многочлена указать невозможно.

Пример 1: Пусть известны значения функции в узлах таблицы

	0	1	2	3	4
	0.1264	0.3487	0.6481	0.4398	0.4643

Требуется вычислить значение функции в точке , используя многочлены Лагранжа 1, 2 и 3 степени. Оценить погрешность интерполирования. Построить графики многочленов Лагранжа 1, 2 и 3 степени.

Решение: Составим интерполяционный многочлен Лагранжа первой степени, замечая, что точка, в которой требуется вычислить значение функции лежит между и , тогда , и .

Канонический вид многочлена Лагранжа первой степени имеет вид: . Вычисления с округлением результатов до четырех знаков после запятой значения многочлена Лагранжа первой степени в точке дают .

Составим интерполяционный многочлен Лагранжа второй степени. Для этого к выбранным ранее точкам и необходимо добавить ближайшую к точку из узлов таблицы, а именно, , и занумеровать полученную последовательность точек. Полученные таким образом точки являются опорными точками для построения многочлена Лагранжа второй степени. Тогда , и

.

Канонический вид многочлена Лагранжа второй степени имеет вид: , и вычисления дают .

Составим интерполяционный многочлен Лагранжа третьей степени. Для этого в качестве опорных точек выберем , так как справа точек в таблице узлов нет. Тогда , и

.

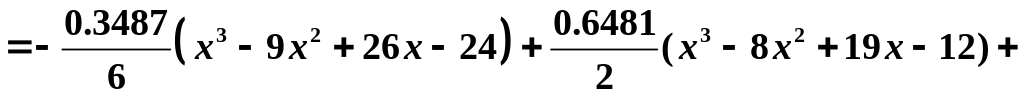
Канонический вид многочлена Лагранжа третьей степени имеет вид: , и вычисления дают .

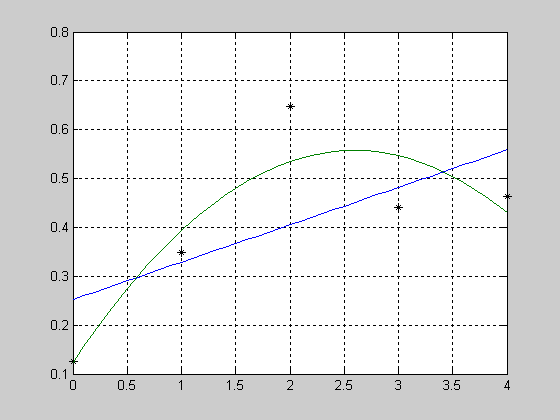
На одном рисунке представлены графики интерполяционных многочленов в форме Лагранжа первой, второй и третьей степени.

Интерполяционный многочлен в форме Ньютона

Определение: Разностными отношениями (разделенными разностями) первого порядка называются величины следующего вида

, ,

,

и т.д. по всей таблице.

Определение: Разностными отношениями (разделенными разностями) второго порядка называются величины следующего вида

, , и т.д.

Аналогичным образом определяются разностные отношения более высоких порядков.

При построении интерполяционного многочлена в форме Ньютона обычно сначала строят таблицу разделенных разностей или разностных отношений, по которой потом строится интерполяционный многочлен

0
1
2
3
4

В данной таблице подчеркнутые величины являются опорными, по которым строится интерполяционный многочлен в форме Ньютона

.

Отметим, что интерполяционным многочленом в форме Лагранжа удобно пользоваться при интерполировании нескольких функций по фиксированной системе узлов, а интерполяционным многочленом в форме Ньютона – по меняющейся системе узлов.

Пример 2: Пусть известны значения функции в узлах таблицы

	0	1	2	3	4
	0.1264	0.3487	0.6481	0.4398	0.4643

Требуется вычислить значение функции в точке , используя многочлены Ньютона 1, 2 и 3 степени. Оценить погрешность интерполирования. Провести сравнение с многочленами Лагранжа соответствующих степеней.

Решение: Занумеруем узлы таблицы в порядке возрастания расстояния до точки , т.е. в следующем порядке: , , , , . Для построения интерполяционного многочлена в форме Ньютона сначала составим таблицу разделенных разностей или разностных отношений:

0	3	0.4398
1	2	0.6481	-0.2083
2	4	0.4643	-0.0919	0.1164
3	1	0.3487	0.0385	-0.1304	0.1234
4	0	0.1264	0.2223	-0.0460	-0.0422

Построим интерполяционные многочлены в форме Ньютона, которые запишем в канонической форме:

,

,

Следует обратить внимание, что погрешность при округлении может давать незначительные расхождения в коэффициентах интерполяционных многочленов в форме Лагранжа и Ньютона, начиная с третьей степени (в данном примере, так как вычисления осуществлялись с точностью до четырех знаков).

Вычисления в точке дают следующие результаты:

, , , .

Погрешность интерполирования

Пусть функция раз дифференцируема на отрезке . Тогда для оценки погрешности интерполяции многочленом Лагранжа степени в точке справедливо равенство

, (2)

На практике пользоваться этим соотношением невозможно, так как точка заранее неизвестна, поэтому в практических расчетах пользуются следствием из этого утверждения, а именно

, , где под понимается интервал, на котором был построен многочлен Лагранжа степени .

Оценку для погрешности интерполяции в точке многочленом Ньютона, не являющейся узловой, можно получить из формулы (2) следующим образом:

Заметим, что в случае, когда величина мала, а функция достаточно гладкая, справедливо приближенное равенство

,

из которого следует, что

.

Оценим погрешность вычислений искомой функции в заданной точке из примера 1. Для многочленов Лагранжа в качестве будем выбирать максимальное по модулю значение функции из заданной таблицы на соответствующем интервале . Тогда

Оценим погрешность вычислений искомой функции в заданной точке из примера 2.

В случае, когда есть возможность выбирать узлы интерполирования, рекомендуется в качестве узлов выбирать корни многочленов Чебышева

, .

Это позволяет минимизировать погрешность интерполирования.

Метод аппроксимации

Среди всех задач приближения функции методом аппроксимации рассмотрим задачу о наилучшем среднеквадратичном приближении.

Наилучшее приближение функций

Пусть задана таблица значений , . функции . Рассмотрим обобщенный многочлен

по системе функций . Если , то имеем задачу интерполирования. Как решить такую задачу, если ?

Образуем в узлах таблицы разности , , вектор характеризует, насколько сильно уклоняется многочлен от табличных значений.

Определим понятие нормы вектора . Наиболее часто употребляются следующие две:

1. ,

2. .

Задача о наилучшем приближении функции состоит в нахождении такого набора коэффициентов , который доставляет минимум норме вектора. При этом первому определению нормы соответствует задача о наилучшем среднеквадратичном приближении, а второму – задача о наилучшем равномерном приближении.

В отличие от метода интерполирования в методе аппроксимации используются все узлы таблицы значений неизвестной функции.

Построение многочленов наилучшего

среднеквадратичного приближения

Требуется найти набор коэффициентов такой, что величина – среднеквадратичное отклонение (невязка) принимает наименьшее значение . Такая задача называется линейной задачей метода наименьших квадратов. Здесь в качестве критерия выбирается условие, что сумма квадратов отклонений во всех узлах сетки таблицы должна быть минимальной, т.е. .

Существует несколько подходов к решению этой задачи. Простейший из них состоит в следующем: нужно использовать условие минимума функции как функции нескольких переменных для получения системы уравнений относительно . Заметим, что минимум функции достигается при том же наборе коэффициентов , что и при достижении минимума функции . Условие минимума функции можно записать следующим образом: . После дифференцирования и перемены порядка суммирования получим систему алгебраических уравнений:

. (3)

В том случае, когда в качестве базовых функций выбираются степенные функции , в роли аппроксимирующей функции выступает полином . Тогда система (3) упрощается: . Описанный метод построения многочленов наилучшего среднеквадратичного приближения части называют методом наименьших квадратов.

Построение многочленов наилучшего

среднеквадратичного приближения

Пример: Зададимся , тогда . Функция в этом случае примет следующий вид , а условие минимума этой функции запишется следующим образом . Тогда приходим к необходимости решения следующей системы линейных алгебраических уравнений

Зададимся , тогда . Тогда приходим к решению следующей системы

Пример: Пусть функция задана таблицей своих значений

	0	1	2	3	4
	0.1264	0.3487	0.6481	0.4398	0.4643

Используя метод наименьших квадратов, аппроксимировать эту функцию многочленами первой и второй степени.

В практических расчетах для построения СЛАУ заполняют вспомогательную таблицу

0	0	0.1264	0	0	0	0	0
1	1	0.3487	1	0.3487	1	1	0.3487
2	2	0.6481	4	1.2962	8	16	2.5924
3	3	0.4398	9	1.3194	27	81	3.9582
4	4	0.4643	16	1.8572	64	256	7.4288
	10	2.0273	30	4.8215	100	354	14.3281

.

Вычислим невязку для :

Аналогично вычисляется невязка для :

.

На рисунке представлены графики кривых многочленов наилучшего среднеквадратичного приближения первой и второй степени.