Метод простой итерации

Чтобы применить метод простой итерации для решения нелинейного уравнения , необходимо преобразовать это уравнение к следующему виду: . Функцию будем называть итерационной функцией. Выберем каким-либо образом приближенное значение корня и подставим его в правую часть последнего уравнения. Получим значение . Подставляя теперь в правую часть уравнения , имеем . Продолжая этот процесс, получим последовательность приближений к корню, вычисляемых по формуле . Итерационный процесс следует продолжать до тех пор, пока после некоторой итерации с номером не будет выполняться неравенство . После этого с погрешностью полагают: . Неравенство является критерием окончания, который на практике заменяет собой априорные и апостериорные оценки погрешности.

Пример: С помощью метода простой итерации вычислить положительный корень уравнения с точностью .

Решение: Результат предыдущего примера дает отрезок локализации . Преобразуем уравнение к виду , где . Заметим, что , 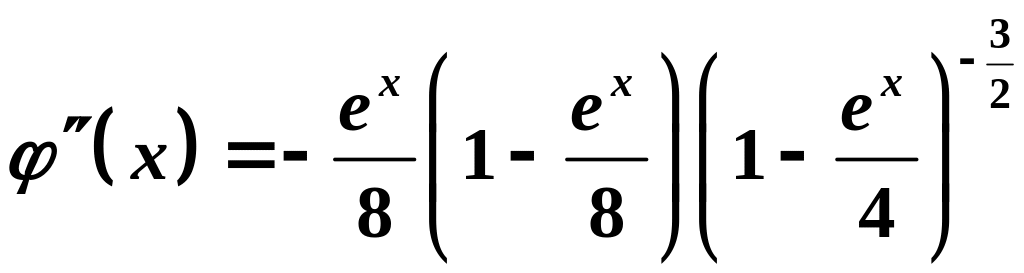. Так как на , то производная монотонно убывает и . Следовательно, условие сходимости выполнено. Возьмем , и будем вести итерации до выполнения критерия . В таблице приведены соответствующие приближения с 10 знаками мантиссы.

0	0.7000000000
1	0.7046714292
2	0.7029968319
3	0.7035984939
4	0.7033824994
5	0.7034600632

Критерий окончания выполняется при . После округления значения до четырех значащих цифр получим .

Метод Ньютона

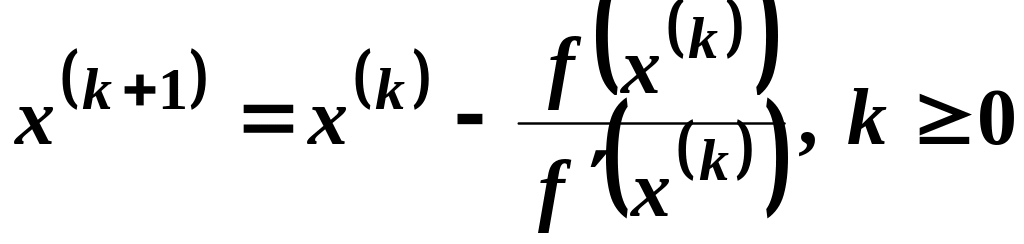Этот метод является одним из наиболее эффективных методов решения самых разных нелинейных уравнений. Расчетная формула метода Ньютона . При выборе начального приближения из достаточно малой окрестности корня метод Ньютона сходится квадратично. Практический критерий окончания итераций метода Ньютона .

Пример: Используя метод Ньютона, найти с точностью положительный корень уравнения .

Решение: Корень уравнения локализован на отрезке . Для имеем . Очевидно, что , то есть – простой корень. Возьмем начальное приближение (середина отрезка) и будем выполнять итерации метода Ньютона по формуле . Результаты первых итераций с 10 знаками мантиссы приведены в таблице.

0	0.5000000000
1	0.7392185177
2	0.7042444088
3	0.7034399951
4	0.7034395712

При вычисления следует прекратить и после округления получим .

В качестве недостатка метода Ньютона следует отметить необходимость вычисления значения производной на каждом шаге итерации. Приведем некоторые расчетные формулы методов решения нелинейного уравнения , которые являются, по существу, модификациями метода Ньютона. Эти методы используют на каждой итерации некоторую процедуру линеаризации нелинейного уравнения.

Упрощенный метод Ньютона: , ;

Метод ложного положения: , , где – фиксированная точка из окрестности корня;

Метод секущих: , ;

Метод Стеффенсена: , .

Модифицированный метод Ньютона для поиска кратных корней:

, .

Контрольные вопросы

1. Из каких этапов состоит численное решение уравнения ?

2. Как графически можно произвести отделение корней?

3. Приведите пример отделения корней нелинейного уравнения.

4. Какая теорема лежит в основе локализации корней уравнений.

5. Назовите известные Вам методы решения нелинейных уравнений.

6. Опишите одну итерацию метода бисекции.

7. Во сколько раз сократится отрезок локализации корня после 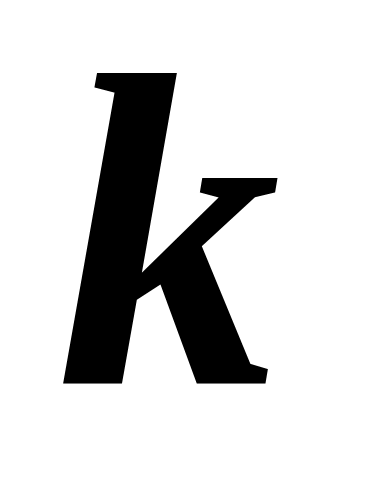- ой итерации метода бисекции.

8. С какой скоростью сходится метод бисекции?

9. Сформулируйте критерий окончания метода бисекции.

10. К какому виду необходимо привести уравнение для применения метода простой итерации.

11. Опишите алгоритм метода простой итерации.

12. Сформулируйте критерий окончания метода простой итерации.

13. По какой формуле рассчитывается очередное приближение к корню нелинейного уравнения по методу Ньютона.

14. Опишите алгоритм метода Ньютона.

15. С какой скоростью сходится метод Ньютона?