Глава 1. Методы решения нелинейных уравнений

Большинство нелинейных уравнений, встречающихся при решении инженерных задач, невозможно решить в явном виде. Приведем в качестве примера следующее уравнение .

В подобных случаях применяются численные методы. Более того, многие из тех задач, которые возможно решить аналитическими методами, нередко гораздо быстрее и эффективнее решаются численными методами с требуемой точностью.

Постановка задачи. Отделение корней.

Пусть дано нелинейное уравнение , где – непрерывно дифференцируемая функция. Решение уравнения состоит из двух этапов:

1) Отделение корней, то есть отыскание областей, в каждой из которых заключен ровно один корень уравнения.

2) Вычисление каждого отделенного корня с заданной точностью.

Отделение корней можно произвести графически с сопутствующим анализом на монотонность, смену знака, выпуклость функции. В частности, полезны следующие сведения из математического анализа:

1) Если – непрерывная строго монотонная функция и , то на отрезке существует единственный корень уравнения .

2) Признак строго монотонного убывания (возрастания) дифференцируемой функции на отрезке : на .

3) Признак строгой выпуклости вверх (вниз) дважды дифференцируемой функции на отрезке : на .

Способы отделения корня:

1) Составляется таблица значений функции на промежутке изменения аргумента , и если окажется, что для соседних значений аргументов значения функции имеют разные знаки, то корень уравнения находится между ними.

2) Строится график функции на промежутке изменения аргумента ; тогда искомые корни находятся в некоторых окрестностях точек пересечения графика с осью .

3) Уравнение заменяется равносильным . Строятся графики функций и ; тогда искомые корни находятся в некоторых окрестностях проекций на ось точек пересечения этих графиков.

Пример: Локализовать корни уравнения .

Решение: Преобразуем уравнение к виду и построим графики функций , .

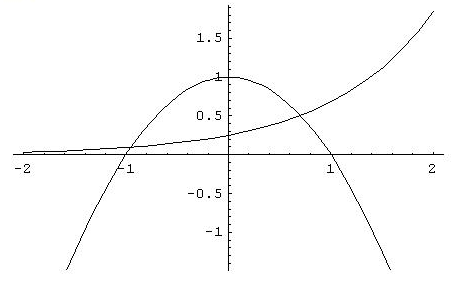
Абсциссы точек пересечения этих графиков являются корнями данного уравнения. Из рисунка видно, что уравнение имеет два корня и , расположенные на отрезках и . На концах данных отрезков функция принимает значения разных знаков, так как . Следовательно, в силу первой теоремы Больцано-Коши на каждом из отрезков и находится по крайней мере один корень.

В дальнейшем будем полагать, что корни уже отделены.

Для вычисления отделенного корня существует множество методов. Из них мы рассмотрим следующие: метод бисекции (метод деления пополам), метод простой итерации и метод Ньютона.

Метод бисекции

Простейшим методом является метод бисекции, называемый также методом деления пополам или методом дихотомии. Он состоит в следующем. Допустим, что удалось найти отрезок , на котором расположен один корень. В качестве начального приближения к корню принимаем середину этого отрезка: . Далее исследуем знаки значений функции на концах отрезков и то есть в точках . Тот из отрезков, на концах которого принимает значения разных знаков, содержит искомый корень; поэтому его принимаем в качестве нового исследуемого отрезка .

Вторую половину отрезка не рассматриваем (так как корня там нет). В качестве первого приближения к корню принимаем середину нового отрезка и т.д. После каждого приближения (итерации) отрезок, на котором расположен корень, уменьшается вдвое, то есть после k-ой итерации он сокращается в 2^k раз.

Опишем очередную -ю итерацию метода. Пусть отрезок уже найден и вычислены значения . Тогда производятся следующие действия:

1. Вычисляется .

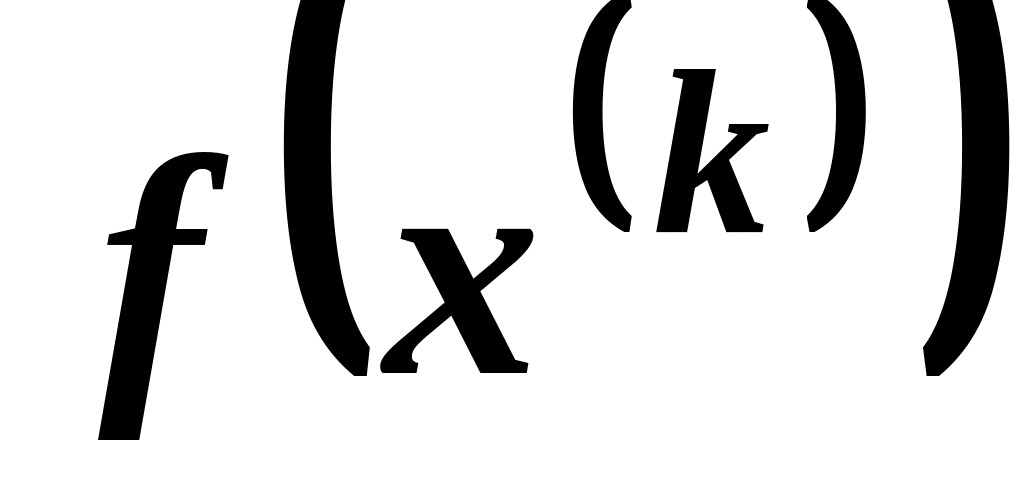2. Если , то в качестве отрезка локализации 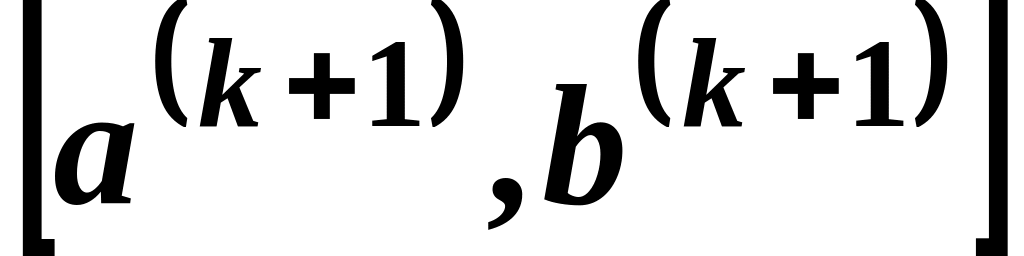принимается отрезок , в противном случае – отрезок .

3. Вычисляется .

Продолжение описанного итерационного процесса дает последовательность отрезков , , содержащий искомый корень. Середина -го отрезка – точка дает приближение к корню , имеющее оценку погрешности . Это означает, что метод бисекции сходится со скоростью геометрической прогрессии, знаменатель которой 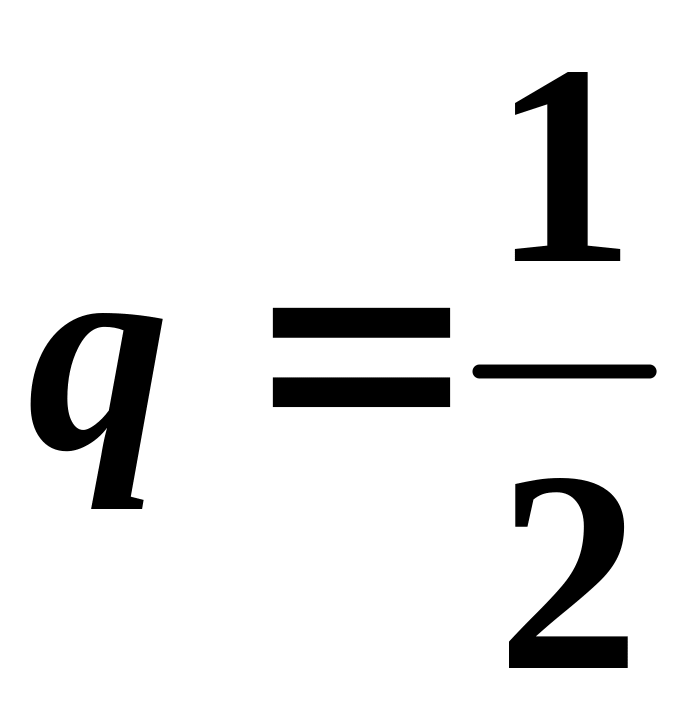. Аналогично оценивают скорости сходимости других методов.

Итерационный процесс следует продолжать до тех пор, пока значение функции после некоторой итерации с номером k+1 не станет по модулю не больше некоторого заданного малого числа , то есть |. После этого с погрешностью полагают: .

Замечание: Другим вариантом условия окончания итераций может служить . Это условие следует из очевидного неравенства .

Пример: Найти методом бисекции с точностью положительный корень уравнения .

Решение: Из предыдущего примера видно, что этот корень был локализован на отрезке , причем . Положим .

I итерация: Вычисляем . Так как , то за очередной отрезок локализации принимаем . Вычисляем .

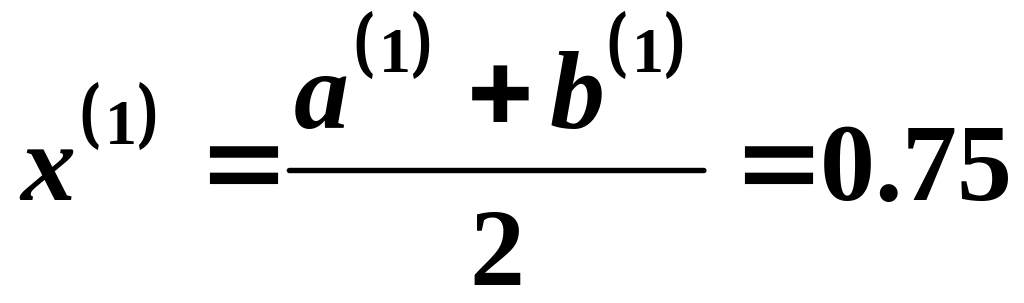II итерация: Вычисляем . Так как , то и .

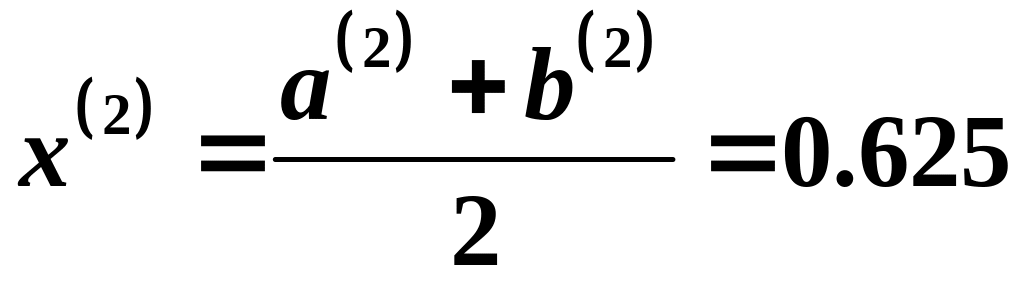Результаты следующих итераций (с четырьмя цифрами после десятичной точки) приведены в таблице

Номер итера-ции			Знак	Знак
0	0.0000	1.0000	+	–	0.5000	1.3513	1.0000
1	0.5000	1.0000	+	–	0.7500	– 0.3670	0.5000
2	0.5000	0.7500	+	–	0.6250	0.5693	0.2500
3	0.6250	0.7500	+	–	0.6875	0.1206	0.1250
4	0.6875	0.7500	+	–	0.7187	– 0.1182	0.0625
5	0.6875	0.7187	+	–	0.7031	0.0222	0.0312
6	0.7031	0.7187	+	–	0.7109		0.0156

При имеем . Следовательно, заданная точность достигнута и можно принять . Окончательно получим .